《2025年万唯中考情境题八年级数学上册苏科版》

请将下面的思维导图补充完整：

答案： 定理内容：如果直角三角形的两条直角边长分别为$a$、$b$，斜边长为$c$，那么$a^{2}+b^{2}=c^{2}$
证明方法：面积法（或拼图法）
逆定理内容：如果三角形的三边长$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$，那么这个三角形是直角三角形
勾股数：能够成为直角三角形三条边长的三个正整数

1. 三角形的三边长分别为 $ a,b,c $,且满足等式 $ (b + c)^2 - a^2 = 2bc $,则该三角形为 (B)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形

答案： B

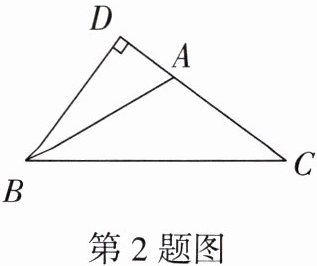
2. 如图,在 $ \triangle ABC $ 中,过点 $ B $ 作 $ CA $ 的垂线交 $ CA $ 的延长线于点 $ D $,已知 $ AB = 13 $,$ AC = 11 $,$ BD = 12 $,则 $ BC $ 的长度为 (D)

A.15
B.16
C.18
D.20

答案： D

3. 如图,在四边形 $ ABCD $ 中,$ AC $ 与 $ BD $ 相交于点 $ O $,且 $ AC \perp BD $,若 $ AD = 2 $,$ BC = 4 $,则 $ AB^2 + CD^2 $ 的值为 (C)
A.8
B.14
C.20
D.26

答案： C

4. 如图,在水平桌面上依次摆着三个正方形,已知位于中间的正方形的面积为 1,两边的正方形面积分别是 $ S_1 $,$ S_2 $,则 $ S_1 + S_2 $ 的值为1。

答案： 1

5. 如图,将长方形 $ ABCD $ 沿 $ AF $ 所在直线折叠,使得点 $ B $ 恰好落在 $ CD $ 边上的点 $ E $ 处,已知 $ CF = 3 \mathrm{cm} $,$ AD = 8 \mathrm{cm} $,则 $ \triangle ADE $ 的面积为 24 cm²。

答案： 24 cm²