《2025年小题狂做九年级数学上册苏科版巅峰版》

6. 已知一个两位数,十位上的数字与个位上的数字之和是5,把这个数个位上的数字与十位上的数字交换后,所得的新数与原来的两位数之积为736,则原来的两位数为23或32.

答案： 23或32

7. 一次篮球锦标赛,每个队都进行了3场比赛后,有6个队被淘汰,剩下的队进行单循环赛. 若一共进行了33场比赛,则共有12个球队.

答案： 12　提示:设共有x个球队。因为前半段比赛每一个球队都进行了3场比赛，所以用$\frac{3}{2}$x场比赛淘汰了6个球队，又因为后半段为单循环比赛，所以可列方程为$\frac{(x - 6)(x - 7)}{2}$ = 33 - $\frac{3}{2}$x。整理，得x² - 10x - 24 = 0，解得x₁ = -2(舍去)，x₂ = 12。所以共有12个球队。

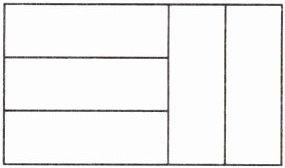
8. 五个完全相同的小矩形拼成如图所示的大矩形,大矩形的面积是$135\ \text{cm}^{2}$,则以小矩形的宽为边长的正方形的面积是9$\text{cm}^{2}$.

答案： 9

9. (徐州市中考)如图是由三个边长分别为6,9,x的正方形所组成的图形. 若直线AB将它分成面积相等的两部分,则x的值为______.

答案：
3或6　提示:构造如图所示的图形，显然矩形CDEF的面积为6×3 = 18。因为直线AB将原图形分成面积相等的两部分，所以$\frac{1}{2}$×9×(6 + 9 + x) - 18 = $\frac{1}{2}$×(6² + 9² + x²)。整理，得x² - 9x + 18 = 0，解得x₁ = 3，x₂ = 6。

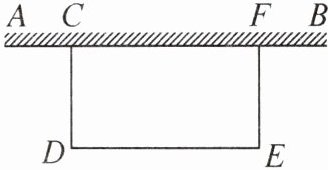
10. 某校广场有一段25 m长的旧围栏. 现打算利用该围栏的一部分(或全部)为一边,围成一块$100\ \text{m}^{2}$的矩形草坪,如图所示,其中四边形CDEF是矩形,$CD＜CF$. 已知整修旧围栏的价格是每米17.5元,建新围栏的价格是每米45元.
(1)若计划修建费为1500元,则能否完成该草坪围栏修建任务？
(2)若计划修建费为1200元,则能否完成该草坪围栏修建任务？若能完成,算出利用旧围栏的长度；若不能完成,请说明理由.

答案： 解:
(1)设CD的长为x m。根据题意，得$\frac{100}{x}$·17.5 + ($\frac{100}{x}$ + 2x)·45 = 1500，即9x² - 150x + 625 = 0，解得x₁ = x₂ = $\frac{25}{3}$。所以CF = 100÷$\frac{25}{3}$ = 12(m)。因为$\frac{25}{3}$＜12＜25，所以能完成该草坪围栏修建任务。
(2)不能完成。理由如下:设CD的长为x m，则$\frac{100}{x}$·17.5 + ($\frac{100}{x}$ + 2x)·45 = 1200，即9x² - 120x + 625 = 0。因为(-120)² - 4×9×625＜0，所以该一元二次方程无实数解，所以不能完成该草坪围栏修建任务。

11. 某超市于今年年初以20元/件的进价购进一批商品,当商品售价为40元/件时,一月份销售了500件,二、三月份该商品十分畅销,销售量持续走高,在售价不变的基础上,三月份的销售量达到了720件.
(1)求二、三月份销售量的月平均增长率.
(2)四月份,超市决定在三月份销售量的基础上采用降价促销的方式回馈顾客,经调查发现,该商品每件每降价1元,销售量增加6件,则当每件商品降价多少元时,商场当月获利11250元？

答案： 解:
(1)设二、三月份销售量的月平均增长率为x，则500(1 + x)² = 720，解得x₁ = 20%，x₂ = -2.2(舍去)。答:二、三月份销售量的月平均增长率是20%。
(2)设每件商品降价y元，则(40 - y - 20)(720 + 6y) = 11250。整理，得y² + 100y - 525 = 0，解得y₁ = 5，y₂ = -105(舍去)。答:当每件商品降价5元时，商场当月获利11250元。