1. 如图,在正八边形 ABCDEFGH 中,连接AD,EH,AE,DH,AE 与 DH 交于点 O.下列结论:①$BC^{2}+EH^{2}= AE^{2}$;②$\frac {AD}{AH}= 2+\sqrt {2}$;③$∠AOD= 135^{\circ }$;④$S_{八边形ABCDEFGH}= 4S_{四边形ABCD}$.其中正确结论的序号是(
A.①②③
B.①②④
C.①③④
D.②③④
C
)A.①②③
B.①②④
C.①③④
D.②③④
答案:
C 提示:易知正八边形每个内角为$\frac{(8 - 2)× 180^\circ}{8}=135^\circ$,中心角为$\frac{360^\circ}{8}=45^\circ$.由正八边形的对称性可知,AE,DH均为其外接圆的直径,点O为圆心,所以$\angle AOH=45^\circ$,$\angle AOD=135^\circ$,故③正确.由四边形ABCD的内角和为$360^\circ$可知,$\angle BAD+\angle CDA=90^\circ$.又由正八边形的对称性可得$\angle BAD=\angle CDA=45^\circ$,易知$BC// AD$,$\angle DAH=90^\circ=\angle ADE$.在$\text{Rt}\triangle ADE$中,$DE^2+AD^2=AE^2$.易得$BC=DE$,$AD=EH$,所以$BC^2+EH^2=AE^2$,故①正确.分别过点B,C作$BK\perp AD$于点K,$CL\perp AD$于点L,并设$KL=BC=AH=\sqrt{2}a$,则$DL=AK=BK=a$,所以$AD=(2+\sqrt{2})a$,所以$\frac{AD}{AH}=\frac{2+\sqrt{2}}{\sqrt{2}}=\sqrt{2}+1$,故②错误.易得$S_{\text{四边形}ABCD}=\frac{1}{2}(BC+AD)\cdot BK=(1+\sqrt{2})a^2$,$S_{\text{矩形}ADEH}=AD\cdot AH=(2\sqrt{2}+2)a^2=2S_{\text{四边形}ABCD}$,所以$S_{\text{八边形}ABCDEFGH}=2S_{\text{四边形}ABCD}+S_{\text{矩形}ADEH}=4S_{\text{四边形}ABCD}$,故④正确.
2. 已知在代数式$ax^{2}+2ax+c$(a,c 是常数)中,x 与该代数式的部分对应值如下表:

根据表中数据,可知关于 x 的方程$ax^{2}+2ax+c= 0$的一个根约为

根据表中数据,可知关于 x 的方程$ax^{2}+2ax+c= 0$的一个根约为
$-2.7$
,另一个根约为$0.7$
.(精确到0.1)
答案:
$-2.7$ $0.7$ 提示:设方程$ax^2+2ax+c=0$的两个根分别为$x_1,x_2$,则$x_1+x_2=-\frac{2a}{a}=-2$.由题中表格可知,该方程其中一个根在$-2.74\sim -2.73$之间,所以关于x的方程$ax^2+2ax+c=0$的一个根约为$-2.7$,则另一个根约为$-2-(-2.7)=0.7$.
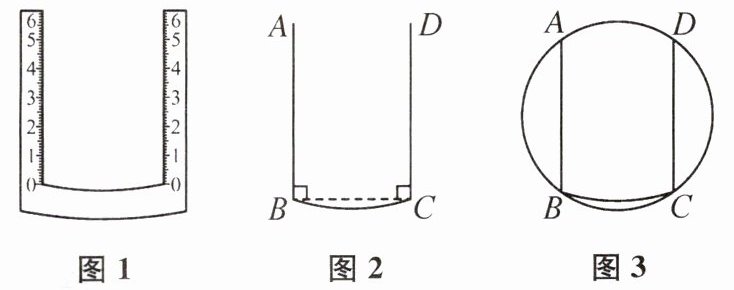
3. 图1是一把“U形”尺,图2是该尺内侧的示意图.已知边$AB⊥BC$,边$CD⊥BC$,$AB= CD= 6cm,BC= 4cm.$
【算一算】
将该尺摆放在一些圆上,测量并计算圆的半径 r.
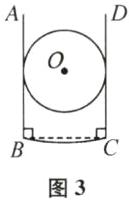
(1) 如图3,点 A,B,C,D 恰好都在圆上,则$r= $______cm.
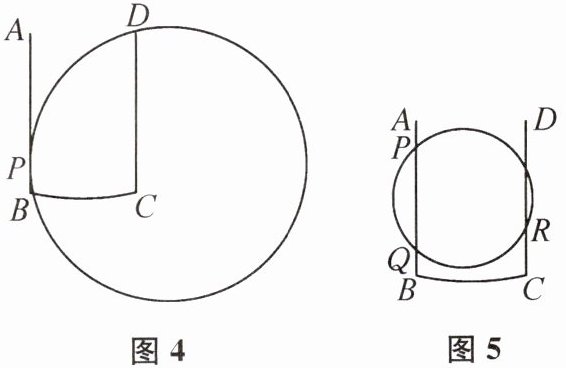
(2) 如图4,该尺的边 AB 与圆相切于点 P,且点 P 在该尺上的读数为1 cm,点 D 在圆上,则$r= $______cm.
(3) 如图5,该尺的边 AB 与圆有两个公共点 P,Q,它们在该尺上的读数分别为5 cm,1 cm,边 CD 与圆也有两个公共点,其中一个公共点 R 在该尺上的读数为2 cm,求 r 的值.
【想一想】
(4) 若将该尺摆放在一个圆上(尺子只摆放一次,圆的圆心未标注),一定可以通过测量并计算出该圆的半径 r 吗?如果一定可以,请说明理由;如果不一定可以,请直接写出可计算出的 r 的最小值和最大值.
【算一算】
将该尺摆放在一些圆上,测量并计算圆的半径 r.
(1) 如图3,点 A,B,C,D 恰好都在圆上,则$r= $______cm.
(2) 如图4,该尺的边 AB 与圆相切于点 P,且点 P 在该尺上的读数为1 cm,点 D 在圆上,则$r= $______cm.
(3) 如图5,该尺的边 AB 与圆有两个公共点 P,Q,它们在该尺上的读数分别为5 cm,1 cm,边 CD 与圆也有两个公共点,其中一个公共点 R 在该尺上的读数为2 cm,求 r 的值.
【想一想】
(4) 若将该尺摆放在一个圆上(尺子只摆放一次,圆的圆心未标注),一定可以通过测量并计算出该圆的半径 r 吗?如果一定可以,请说明理由;如果不一定可以,请直接写出可计算出的 r 的最小值和最大值.


答案:
解:
(1)$\sqrt{13}$ 提示:连接AC.由题意可知$\angle ABC=90^\circ$,所以AC为直径.由勾股定理,得$AC=\sqrt{AB^2+BC^2}=2\sqrt{13}\ \text{cm}$,所以$r=\sqrt{13}\ \text{cm}$.
(2)$\frac{41}{8}$ 提示:设圆心为点O,连接OP,交CD于点Q,连接BC,OD,则$OP\perp AB$.由题意可知,$BP=1\ \text{cm}$,四边形BCQP为矩形,所以$PQ=BC=4\ \text{cm}$,$CQ=BP=1\ \text{cm}$,所以$OQ=OP-PQ=(r-4)\ \text{cm}$,$DQ=CD-CQ=5\ \text{cm}$.在$\text{Rt}\triangle DOQ$中,$OD^2=OQ^2+DQ^2$,即$r^2=(r-4)^2+5^2$,解得$r=\frac{41}{8}$.
(3)设圆心为点O,过点O作$OM\perp AB$于点M,延长MO交CD于点N,连接OQ,OR,BC.易证四边形BCNM为矩形.由题意可知,$PB=5\ \text{cm}$,$BQ=1\ \text{cm}$,$CR=2\ \text{cm}$,所以$PQ=PB-BQ=4\ \text{cm}$,所以$MQ=\frac{1}{2}PQ=2\ \text{cm}$,所以$CN=BM=MQ+BQ=3\ \text{cm}$,所以$NR=CN-CR=1\ \text{cm}$.设$OM=x\ \text{cm}$,则$ON=(4-x)\ \text{cm}$.由勾股定理,得$OQ^2=OM^2+MQ^2$,$OR^2=ON^2+NR^2$,即$r^2=x^2+2^2$,$r^2=(4-x)^2+1^2$,所以$x^2+2^2=(4-x)^2+1$,解得$x=\frac{13}{8}$,所以$r=OQ=\sqrt{(\frac{13}{8})^2+2^2}=\frac{5\sqrt{17}}{8}\ \text{cm}$.
(4)若将该尺摆放在一个圆上(尺子只摆放一次,圆的圆心未标注),不一定可以通过测量并计算出该圆的半径r,半径r的最小值为$2\ \text{cm}$,最大值为$\frac{13}{2}\ \text{cm}$. 提示:如图1,当圆的直径小于BC的长度时,此时“U形”尺上没有任何读数,则无法测量并计算出圆的半径.
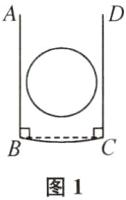
如图2,当圆与AB和CD其中一边相交时,也相当于只测得一条弦的长度,也无法得到圆的半径r.当圆较大,“U形”尺完全包含于圆内时,也无法测得圆的半径.因为BC没有刻度,所以要能够测出圆的半径,则圆与AB,CD都要有交点.如图3,当$\odot O$与AB,CD均相切时,直径等于BC的长为$4\ \text{cm}$,即$\odot O$的半径r的最小值为$2\ \text{cm}$.
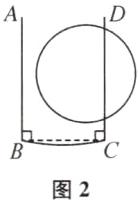
如图4,当满足题意的圆最大时,不妨设圆心O在边CD的右侧,要想能测出圆的半径,$\odot O$至少要与AB相切,与CD有交点.令$\odot O$与AB相切于点P,与CD交于边界点D.由题意可知,$QD\leqslant 6\ \text{cm}$.类比
(2)可知,$PQ=4\ \text{cm}$,则$OQ=(r-4)\ \text{cm}$.由勾股定理,可得$QD^2=OD^2-OQ^2$,所以$r^2-(r-4)^2\leqslant 36$,所以$r\leqslant \frac{13}{2}$,则$\odot O$的半径r的最大值为$\frac{13}{2}\ \text{cm}$.

解:
(1)$\sqrt{13}$ 提示:连接AC.由题意可知$\angle ABC=90^\circ$,所以AC为直径.由勾股定理,得$AC=\sqrt{AB^2+BC^2}=2\sqrt{13}\ \text{cm}$,所以$r=\sqrt{13}\ \text{cm}$.
(2)$\frac{41}{8}$ 提示:设圆心为点O,连接OP,交CD于点Q,连接BC,OD,则$OP\perp AB$.由题意可知,$BP=1\ \text{cm}$,四边形BCQP为矩形,所以$PQ=BC=4\ \text{cm}$,$CQ=BP=1\ \text{cm}$,所以$OQ=OP-PQ=(r-4)\ \text{cm}$,$DQ=CD-CQ=5\ \text{cm}$.在$\text{Rt}\triangle DOQ$中,$OD^2=OQ^2+DQ^2$,即$r^2=(r-4)^2+5^2$,解得$r=\frac{41}{8}$.
(3)设圆心为点O,过点O作$OM\perp AB$于点M,延长MO交CD于点N,连接OQ,OR,BC.易证四边形BCNM为矩形.由题意可知,$PB=5\ \text{cm}$,$BQ=1\ \text{cm}$,$CR=2\ \text{cm}$,所以$PQ=PB-BQ=4\ \text{cm}$,所以$MQ=\frac{1}{2}PQ=2\ \text{cm}$,所以$CN=BM=MQ+BQ=3\ \text{cm}$,所以$NR=CN-CR=1\ \text{cm}$.设$OM=x\ \text{cm}$,则$ON=(4-x)\ \text{cm}$.由勾股定理,得$OQ^2=OM^2+MQ^2$,$OR^2=ON^2+NR^2$,即$r^2=x^2+2^2$,$r^2=(4-x)^2+1^2$,所以$x^2+2^2=(4-x)^2+1$,解得$x=\frac{13}{8}$,所以$r=OQ=\sqrt{(\frac{13}{8})^2+2^2}=\frac{5\sqrt{17}}{8}\ \text{cm}$.
(4)若将该尺摆放在一个圆上(尺子只摆放一次,圆的圆心未标注),不一定可以通过测量并计算出该圆的半径r,半径r的最小值为$2\ \text{cm}$,最大值为$\frac{13}{2}\ \text{cm}$. 提示:如图1,当圆的直径小于BC的长度时,此时“U形”尺上没有任何读数,则无法测量并计算出圆的半径.

如图2,当圆与AB和CD其中一边相交时,也相当于只测得一条弦的长度,也无法得到圆的半径r.当圆较大,“U形”尺完全包含于圆内时,也无法测得圆的半径.因为BC没有刻度,所以要能够测出圆的半径,则圆与AB,CD都要有交点.如图3,当$\odot O$与AB,CD均相切时,直径等于BC的长为$4\ \text{cm}$,即$\odot O$的半径r的最小值为$2\ \text{cm}$.


如图4,当满足题意的圆最大时,不妨设圆心O在边CD的右侧,要想能测出圆的半径,$\odot O$至少要与AB相切,与CD有交点.令$\odot O$与AB相切于点P,与CD交于边界点D.由题意可知,$QD\leqslant 6\ \text{cm}$.类比
(2)可知,$PQ=4\ \text{cm}$,则$OQ=(r-4)\ \text{cm}$.由勾股定理,可得$QD^2=OD^2-OQ^2$,所以$r^2-(r-4)^2\leqslant 36$,所以$r\leqslant \frac{13}{2}$,则$\odot O$的半径r的最大值为$\frac{13}{2}\ \text{cm}$.

查看更多完整答案,请扫码查看


