《2025年小题狂做九年级数学上册苏科版巅峰版》

10. 在一个不透明的围棋盒子中有 x 颗白色棋子和 y 颗黑色棋子,它们除颜色外其他都相同.从盒子中随机取出 1 颗棋子,是黑色棋子的概率为$\frac {2}{3}.$
(1) 请写出 y 与x 之间的函数关系式.
(2) 现在往盒子中再放进 5 颗白色棋子和 1 颗黑色棋子,这时随机取出白色棋子的概率为$\frac {1}{2}$,请求出 x 和 y 的值.

答案：
(1)根据题意，得$\frac{y}{x + y} = \frac{2}{3}$，化简，得$y = 2x$（$x$为正整数）。
(2)根据题意，得$\begin{cases} \frac{y}{x + y} = \frac{2}{3}, \\ \frac{x + 5}{x + 5 + y + 1} = \frac{1}{2}, \end{cases}$解得$\begin{cases} x = 4, \\ y = 8. \end{cases}$所以$x$的值为$4$，$y$的值为$8$。

11. 已知关于 x 的一元二次方程$x^{2}+ax+bn= 0(1≤n≤3$,n 为整数),其中 a 是从 2,4,6 这三个数中任取的一个数,b 是从 1,3,5 这三个数中任取的一个数,定义"方程有实数根"为事件$A_{n}(n= 1,2,3)$,当$A_{n}$的概率最小时,n 的所有可能值为______2,3。

答案： 2,3 提示:当$n = 1$时，方程的根的判别式为$a^{2} - 4b$。将$a$，$b$各取一个数代入，共$9$种情况，其中使$a^{2} - 4b \geq 0$的有$6$种，所以$P(A_{1}) = \frac{6}{9} = \frac{2}{3}$。同理可得，当$n = 2$时，$P(A_{2}) = \frac{3}{9} = \frac{1}{3}$；当$n = 3$时，$P(A_{3}) = \frac{3}{9} = \frac{1}{3}$。故当$A_{n}$的概率最小时，$n$的所有可能值为$2$，$3$。

12. 如图,这是一台名为帕斯卡三角的仪器,当实心小球从入口落下,它依次碰到每层菱形挡块时,会等可能地向左或向右落下.
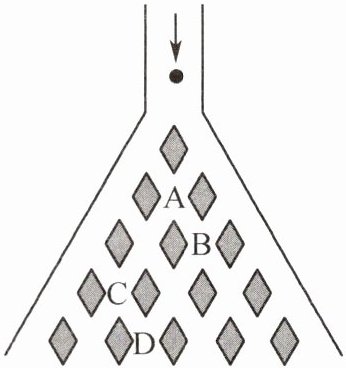
(1) 分别求出小球通过第 2 层的 A 位置、第 3 层的 B 位置、第 4 层的 C 位置、第 5 层的 D 位置的概率.
(2) 设菱形挡块的层数为 n,则小球通过第 n 层的从左边算起第 2 个位置的概率是多少?

答案：
(1)因为实心小球在碰到菱形挡块时，向左或向右下落是等可能的，所以经过一个菱形挡块后向左或向右下落的概率各是原概率的一半。
画出帕斯卡三角树状图如图所示。
第一层 1 1
第二层 1 2 1
第三层 1 3 3 1
第四层 1 4 6 4 1
第五层 1 5 10 10 5 1
所以通过$A$位置的概率为$\frac{2}{1 + 2 + 1} = \frac{1}{2}$；通过$B$位置的概率为$\frac{3}{1 + 3 + 3 + 1} = \frac{3}{8}$；通过$C$位置的概率为$\frac{4}{1 + 4 + 6 + 4 + 1} = \frac{1}{4}$；通过$D$位置的概率为$\frac{10}{1 + 5 + 10 + 10 + 5 + 1} = \frac{5}{16}$。
(2)根据
(1)可知，通过第$n$层的所有可能情况数是$2^{n}$，通过第$n$层的从左边算起第$2$个位置的情况数是$n$，所以通过第$n$层的从左边算起第$2$个位置的概率为$\frac{n}{2^{n}}$。