《2025年小题狂做九年级数学上册苏科版巅峰版》

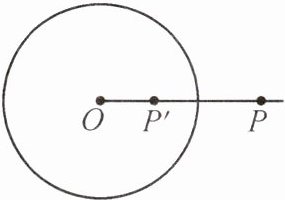
9. (淮安市洪泽区期中节选)如图,$\odot O$的半径为 r(r＞0),若点 P'在射线 OP 上(点 P'可以和射线端点重合),满足$OP'+OP= 2r$,则称 P'是点 P 关于$\odot O$的"反演点".已知$\odot O$的半径为8.
(1) 若$OP_{1}= 17,OP_{2}= 12,OP_{3}= 4$,则点$P_{1},P_{2},P_{3}中存在关于\odot O$的"反演点"的是点______$P_{2},P_{3}$.
(2) 若点 P 关于$\odot O$的"反演点"在$\odot O$内,则 OP 长的取值范围是______$8＜OP≤16$.

答案：
(1)$P_{2},P_{3}$ 提示:根据“反演点”的定义可知，当$0＜OP≤2r$时，点P存在关于⊙O的“反演点”.因为$OP_{1}=17,OP_{2}=12,OP_{3}=4,2r=2×8=16$，所以点$P_{2},P_{3}$存在关于⊙O的“反演点”.
(2)$8＜OP≤16$

10. 【问题情境】
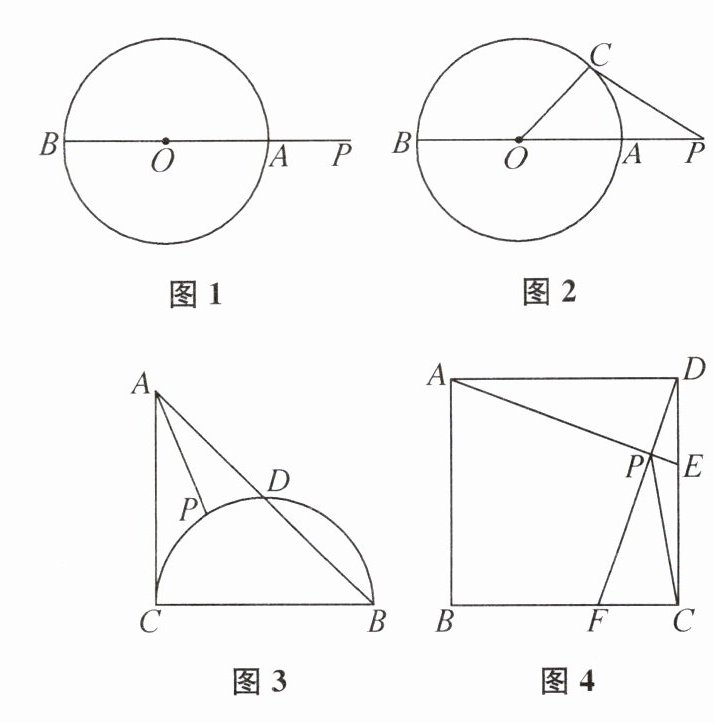
如图1,P 是$\odot O$外一点,直线 PO 交$\odot O$于 A,B 两点,则 PA 的长是点 P 到$\odot O$上的点的最短距离.
【初步探究】
(1) 如图2,小明为了证明【问题情境】中的结论,给出如下思路:在$\odot O$上任取一点 C(不与 A,B 两点重合),连接 PC,OC.请你根据小明的思路继续思考,完成 PA＜PC 的证明过程.
【直接运用】
(2) 如图3,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ},AC= BC= 4$,以 BC 为直径的半圆交 AB 于点 D,P 是$\overset{\frown}{CD}$上的一个动点,连接 AP,求出线段 AP 长度的最小值.
【构造运用】
(3) 如图4,在正方形 ABCD 中,AD= 6,点 E,F 分别从 D,C 两点同时出发,以相同的速度在边 DC,CB 上移动,连接 AE,DF 交于点 P,连接 CP,由于点 E,F 的移动,使得点 P 也随之移动,请求出线段 CP 长度的最小值.

答案：
(1)证明:因为$PO=PA+OA,PO＜PC+OC,OA=OC$，所以$PA＜PC$.
(2)解:取BC的中点E，连接AE，交半圆于点$P_{2}$.由【问题情境】中给出的结论，易得$AP_{2}$的长是AP长的最小值.在$Rt\triangle ABC$中，因为$∠ACB=90^{\circ },AC=BC=4,P_{2}E=CE=\frac {1}{2}BC=2$，所以$AE=\sqrt {AC^{2}+CE^{2}}=2\sqrt {5}$，所以$AP_{2}=2\sqrt {5}-2$，即线段AP长度的最小值为$2\sqrt {5}-2$.
(3)解:因为四边形ABCD是正方形，所以$AD=DC=6,∠ADC=∠DCF=90^{\circ }$.由题意可知，$DE=CF$，易证$\triangle ADE\cong \triangle DCF(SAS)$，所以$AE=DF,∠DAE=∠CDF$.因为$∠CDF+∠ADF=90^{\circ }$，所以$∠DAE+∠ADF=90^{\circ }$，所以$∠APD=90^{\circ }$.设AD的中点为Q.根据“直角三角形斜边上的中线等于斜边的一半”可知$QP=QD=QA$，所以点P在以AD为直径的圆弧上运动，$DQ=\frac {1}{2}AD=3$.连接QC交弧于点P，此时CP的长度最小.在$Rt\triangle QDC$中，$QC=\sqrt {DC^{2}+DQ^{2}}=3\sqrt {5}$，所以$CP=QC - QP=3\sqrt {5}-3$，即线段CP长度的最小值为$3\sqrt {5}-3$.

11. 如图,P 为函数$y= \frac{36}{x}(x＞0)$图像上的任意一点,$\odot P$的半径为 2,点 A(4,0),B(8,0),Q 是$\odot P$上的动点,C 是 QB 的中点,则 AC 长的最小值是______$3\sqrt{2}-1$.
 

答案： $3\sqrt {2}-1$ 提示:如图，连接OP交⊙P于点$Q'$，连接$BQ'$，取$BQ'$的中点$C'$，连接$AC'$，此时AC的长最小，为$AC'$的长.设点P的坐标为$(x,\frac {36}{x})$，则$OP=\sqrt {x^{2}+(\frac {36}{x})^{2}}=\sqrt {(x - \frac {36}{x})^{2}+2x\cdot \frac {36}{x}}=\sqrt {(x - \frac {36}{x})^{2}+72}≥6\sqrt {2}$.因为点$A(4,0),B(8,0)$，C是QB的中点，所以$OA=AB,CB=CQ$，所以$AC=\frac {1}{2}OQ$.当点Q运动到点$Q'$时，OQ的长最小，此时AC的长最小值为$AC'=\frac {1}{2}OQ'=\frac {1}{2}(6\sqrt {2}-PQ')=3\sqrt {2}-1$.

12. 如图,在矩形 ABCD 中,AB= 4,BC= 5,以 AB 为直径作$\odot O$,在直线 BC 上取点 P,使得$\odot O$上的动点 E 到点 P 的最小距离为$2\sqrt{2}-2$,则 DP 的长为5或$\sqrt{65}$.

答案： 5或$\sqrt {65}$ 提示:连接OE,PE,OP,则$OE=OB=\frac {1}{2}AB=2,PE≥OP - OE=OP - 2$.所以当点O,E,P依次共线时，动点E到点P的距离最小.①如图1，当点P在点B的右侧时，因为$PE=2\sqrt {2}-2$，所以$OP=2\sqrt {2}$.因为四边形ABCD是矩形，所以$∠OBP=90^{\circ }$，所以$PB=\sqrt {OP^{2}-OB^{2}}=2$.因为$BC=5$，所以$PC=BC - PB=3$.在$Rt\triangle DCP$中，由勾股定理，得$DP=\sqrt {CD^{2}+PC^{2}}=5$.②如图2，当点P在点B的左侧时，同理可得$PB=2$，所以$PC=BC+PB=7$.在$Rt\triangle DCP$中，由勾股定理，得$DP=\sqrt {CD^{2}+PC^{2}}=\sqrt {65}$.综上所述，DP的长为5或$\sqrt {65}$