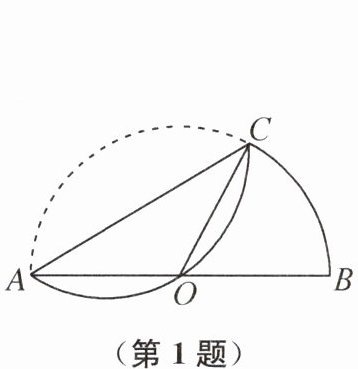
1. 如图,AB 是半圆O的直径,以弦AC为折痕折叠$\overset{\frown}{AC}$后,恰好经过点O,连接OC,则$∠AOC$等于( )
A.$120^{\circ }$
B.$125^{\circ }$
C.$130^{\circ }$
D.$145^{\circ }$

A.$120^{\circ }$
B.$125^{\circ }$
C.$130^{\circ }$
D.$145^{\circ }$
答案:
A 提示:如图,点O关于直线AC的对称点是Q,连接OQ,交AC于点M,则AC垂直平分OQ,即AQ=AO,OQ⊥AC.因为OQ=OA,所以OQ=AQ=OA,所以△AQO是等边三角形,所以∠AOQ=60°.又因为OQ⊥AC,OA=OC,所以∠COQ=∠AOQ=60°,所以∠AOC=60°+60°=120°.

A 提示:如图,点O关于直线AC的对称点是Q,连接OQ,交AC于点M,则AC垂直平分OQ,即AQ=AO,OQ⊥AC.因为OQ=OA,所以OQ=AQ=OA,所以△AQO是等边三角形,所以∠AOQ=60°.又因为OQ⊥AC,OA=OC,所以∠COQ=∠AOQ=60°,所以∠AOC=60°+60°=120°.

2. 如图,已知直线PA交$\odot O$于A,B两点,AE是$\odot O$的直径,C为$\odot O$上一点,且AC平分$∠PAE$,过点C作$CD⊥PA$,垂足为D,且$DC+DA= 12$,$\odot O$的直径为20,则AB的长等于(
A.8
B.12
C.16
D.18
B
)A.8
B.12
C.16
D.18
答案:
B 提示:连接OC,过点O作OF⊥AB,垂足为F.因为OA=OC,所以∠OCA=∠OAC.因为AC平分∠PAE,所以∠DAC=∠OAC.所以∠DAC=∠OCA,所以PB//OC.又因为CD⊥PA,OF⊥AB,所以四边形DCOF为矩形,所以OC=DF,OF=CD.设AD=x,则OF=CD=12 - x.因为⊙O的直径为20,所以DF=OC=10.所以AF=10 - x.在Rt△AOF中,由勾股定理,得AF²+OF²=OA²,即(10 - x)²+(12 - x)²=10²,解得x₁=4,x₂=18(不合题意,舍去).所以AF=10 - 4=6,所以AB=2AF=12.
3. 如图,在平面直角坐标系中,$\odot P的圆心坐标是(-3,a)(a>3)$,半径为3,函数$y= -x的图像被\odot P$截得的弦AB的长为$4\sqrt {2}$,则a的值是(
A.4
B.$3+\sqrt {2}$
C.$3\sqrt {2}$
D.$3+\sqrt {3}$
B
)A.4
B.$3+\sqrt {2}$
C.$3\sqrt {2}$
D.$3+\sqrt {3}$
答案:
B 提示:过点P分别作PC⊥x轴于点C,交AB于点D,PE⊥AB于点E,连接PB.因为⊙P的圆心坐标是(-3,a),所以OC=3,PC=a.把x=-3代入y=-x,得y=3.所以点D(-3,3).易得CD=3=OC,所以△OCD为等腰直角三角形,所以∠CDO=45°,所以∠PDE=45°.又因为PE⊥AB,所以△PED也为等腰直角三角形,BE=1/2AB=2√2.在Rt△PBE中,由勾股定理,得PE=√(PB² - BE²)=1.所以PD=√2,所以PC=CD+PD=3+√2,即a=3+√2.
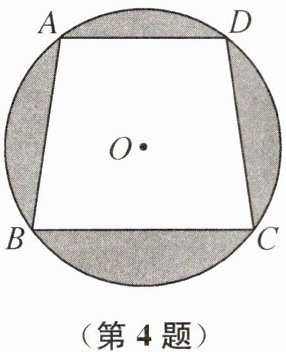
4.(2024南京市建邺区期中)如图,$\odot O$的直径为10,弦AD,BC在圆心的两侧,且$AD// BC$,$AD= 6$,$BC= 8$,则图中阴影部分的面积为______.

答案:
25π - 49 提示:如图,过点O作OF⊥BC于点F,交AD于点E,连接OA,OB.因为AD//BC,所以AD⊥EF.因为AD=6,BC=8,⊙O的直径为10,所以AE=3,BF=4,OA=OB=5,所以OE=√(OA² - AE²)=4,OF=√(OB² - BF²)=3,所以EF=OE+OF=7,所以S_阴影=S_⊙O - S_梯形ABCD=π×5² - 1/2×(6+8)×7=25π - 49.

25π - 49 提示:如图,过点O作OF⊥BC于点F,交AD于点E,连接OA,OB.因为AD//BC,所以AD⊥EF.因为AD=6,BC=8,⊙O的直径为10,所以AE=3,BF=4,OA=OB=5,所以OE=√(OA² - AE²)=4,OF=√(OB² - BF²)=3,所以EF=OE+OF=7,所以S_阴影=S_⊙O - S_梯形ABCD=π×5² - 1/2×(6+8)×7=25π - 49.

5. 如图,在平面直角坐标系中,$\odot O$的半径为5,弦AB的长为6,过点O作$OC⊥AB$于点C,$\odot O$内一点D的坐标为$(-2,1)$.当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是______
4 - √5
.
答案:
4 - √5 提示:连接OB,则OB=5,BC=1/2AB=3.易得OC=4.由题图易知,当CB在第二象限时,会出现最小值的情况,此时过点D作DE⊥AB于点E,连接OD,OE,则OD+DE≥OE≥OC,即DE≥OC - OD,所以当OC经过点D时,点D到AB的距离DE的值最小.因为点D(-2,1),所以OD=√(2²+1²)=√5.所以点D到AB的距离的最小值为4 - √5.(注:当CB在第四象限时,会出现最大值)
6. 如图,AD是$\triangle ABC$的高,作以点O为圆心的两个同心圆,小圆经过点A,D,大圆经过点B,C.若小圆的半径为6,大圆的半径为10,则$AB^{2}+BC^{2}+AC^{2}= $
672
.
答案:
672 提示:设小圆与CD交于点E,连接OA,OB,OC,OD,OE,过点O作OF⊥BC于点F.因为AD⊥BC,所以∠ADE=90°,易知OA=OD=OE,所以∠OAD=∠ODA,∠ODE=∠OED,所以∠AOD+∠DOE=180° - 2∠ODA+180° - 2∠ODE=180°,即点A,O,E在同一直线上.由垂径定理可知,DF=EF,BF=CF.易知OF为△ADE的中位线,所以OF=1/2AD.设OF=x,则DF=EF=√(36 - x²),BF=CF=√(100 - x²),BD=BF - DF=√(100 - x²) - √(36 - x²),CD=CF+DF=√(100 - x²)+√(36 - x²),AD=2x.所以AB²=AD²+BD²=2x²+136 - 2√(100 - x²)·√(36 - x²),AC²=AD²+CD²=136+2x²+2√(100 - x²)·√(36 - x²),BC²=(2BF)²=4(100 - x²),所以AB²+BC²+AC²=672.
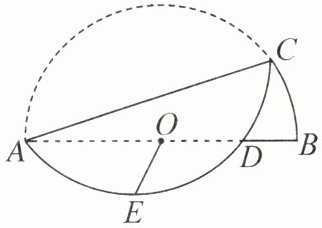
7. 如图,在半圆O中,直径$AB= 4$,C是半圆上一点,将$\overset{\frown}{AC}$沿弦AC折叠交AB于点D,E是$\overset{\frown}{AD}$的中点,连接OE,则OE长的最小值为______.

答案:
2√2 - 2 提示:如图,连接OC,CE,把⌢AEC所在的圆补全为⊙F并连接FC,FE,可知点F与点O关于AC对称,半径为2,所以∠FCA=∠ACO.因为OA=OC,所以∠ACO=∠CAO.所以∠FCA=∠CAO,所以CF//AB.因为E是⌢AD的中点,所以FE⊥AB,所以∠F=∠BGE=90°.因为FC=FE=2,所以在Rt△CFE中,由勾股定理,得EC=√(FC²+FE²)=2√2.因为OE≥EC - OC(当点C,O,E依次共线时,取等号),即OE≥2√2 - 2,所以OE长的最小值为2√2 - 2.

2√2 - 2 提示:如图,连接OC,CE,把⌢AEC所在的圆补全为⊙F并连接FC,FE,可知点F与点O关于AC对称,半径为2,所以∠FCA=∠ACO.因为OA=OC,所以∠ACO=∠CAO.所以∠FCA=∠CAO,所以CF//AB.因为E是⌢AD的中点,所以FE⊥AB,所以∠F=∠BGE=90°.因为FC=FE=2,所以在Rt△CFE中,由勾股定理,得EC=√(FC²+FE²)=2√2.因为OE≥EC - OC(当点C,O,E依次共线时,取等号),即OE≥2√2 - 2,所以OE长的最小值为2√2 - 2.

8. 已知,$\triangle ABC内接于\odot O$,AC为$\odot O$的直径,D为优弧BC的中点.
(1)如图1,连接OD,求证:$DO⊥BC$.
(2)如图2,过点D作$DE⊥AC$,垂足为E.若$AE= 3$,$BC= 8$,求$\odot O$的半径.
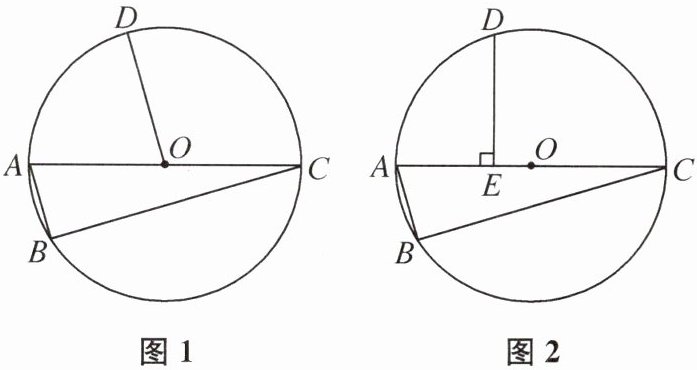
(1)如图1,连接OD,求证:$DO⊥BC$.
(2)如图2,过点D作$DE⊥AC$,垂足为E.若$AE= 3$,$BC= 8$,求$\odot O$的半径.

答案:
(1)证明:如图1,延长DO交BC于点F,连接BD,CD,OB.因为D为优弧BC的中点,所以⌢BD=⌢CD.所以BD=CD,所以点D在线段BC的垂直平分线上.因为OB=OC,所以点O在线段BC的垂直平分线上.所以DF是线段BC的垂直平分线,所以DF⊥BC,即DO⊥BC.

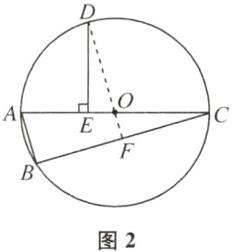
(2)解:如图2,连接DO并延长交BC于点F,设⊙O的半径为x.因为D为优弧BC的中点,所以⌢BD=⌢CD.由
(1)可知DF⊥CB,所以∠OFC=90°,CF=BF=1/2BC=4.因为DE⊥AC,所以∠OED=90°=∠OFC.因为OC=OD,∠DOE=∠COF,所以△DOE≌△COF(AAS),所以OF=OE=OA - AE=x - 3.在Rt△COF中,OC²=OF²+CF²,即x²=(x - 3)²+4²,解得x=25/6,所以⊙O的半径为25/6.
(1)证明:如图1,延长DO交BC于点F,连接BD,CD,OB.因为D为优弧BC的中点,所以⌢BD=⌢CD.所以BD=CD,所以点D在线段BC的垂直平分线上.因为OB=OC,所以点O在线段BC的垂直平分线上.所以DF是线段BC的垂直平分线,所以DF⊥BC,即DO⊥BC.


(2)解:如图2,连接DO并延长交BC于点F,设⊙O的半径为x.因为D为优弧BC的中点,所以⌢BD=⌢CD.由
(1)可知DF⊥CB,所以∠OFC=90°,CF=BF=1/2BC=4.因为DE⊥AC,所以∠OED=90°=∠OFC.因为OC=OD,∠DOE=∠COF,所以△DOE≌△COF(AAS),所以OF=OE=OA - AE=x - 3.在Rt△COF中,OC²=OF²+CF²,即x²=(x - 3)²+4²,解得x=25/6,所以⊙O的半径为25/6.
查看更多完整答案,请扫码查看


