《2025年小题狂做九年级数学上册苏科版巅峰版》

1. 如图,在矩形 ABCD 中,AB= 4,以点 B 为圆心,BA 的长为半径画弧交 BC 于点 E,以点 O 为圆心的$\odot O与\widehat {AE}$,边 AD,DC 都相切. 把扇形 BAE 制作成一个圆锥的侧面,该圆锥的底面圆恰好是$\odot O$,则 AD 的长为 (D)
A.4
B.$\frac {9}{2}$
C.$\frac {11}{2}$
D.5

答案： D 提示:因为 AB=4,∠B=90°,所以$\overset{\frown}{AE}$的长为$\frac{90\pi×4}{180}=2\pi$.所以$\odot O$的半径为1.设$\odot O$与边AD,DC分别相切于点F,G,连接OG,连接FO并延长,交BC于点H,则四边形ABHF、四边形CDFH和四边形CGOH都是矩形,四边形DFOG是正方形.连接BO,在Rt△BOH中,易知BO=5,OH=3,可得BH=4=BE,所以点H与点E重合,所以AD=BC=BE+CE=BE+OG=5.

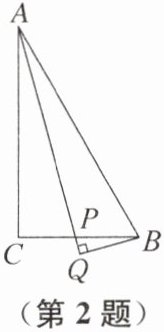
2. (南京市秦淮区期中)如图,在$\triangle ABC$中,$∠C= 90^{\circ },∠BAC= 30^{\circ },AB= 2$,点 P 从点 C 出发,沿 CB 运动到点 B 停止,过点 B 作射线 AP 的垂线,垂足为 Q,则点 Q 运动的路径长为 (D)

A.$\frac {2\sqrt {3}}{3}$
B.$\sqrt {3}$
C.$\frac {\sqrt {3}π}{6}$
D.$\frac {π}{3}$

答案： D 提示:因为AQ⊥BQ,所以点Q在以AB为直径的$\odot O$(O为AB的中点)上运动.连接OC,则$OB=OC=\frac{1}{2}AB=1$.由点P的起点和终点位置可知,点Q运动的路径为$\overset{\frown}{BC}$.因为∠ACB=90°,所以点A,C,Q,B均在$\odot O$上,所以∠COB=2∠BAC=60°.所以点Q运动的路径长为$\frac{60\pi×1}{180}=\frac{\pi}{3}$.

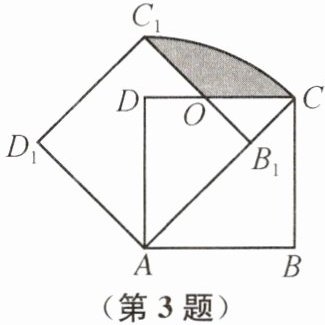
3. 如图,将边长为1的正方形 ABCD 绕点 A 逆时针旋转$45^{\circ }后得到正方形AB_{1}C_{1}D_{1},边B_{1}C_{1}$与 CD 交于点 O,则图中阴影部分的面积为 (B)

A.$\frac {π}{4}-2-\sqrt {2}$
B.$\frac {π}{4}-2+\sqrt {2}$
C.$\frac {π}{4}+\frac {1}{2}$
D.$\frac {π}{4}-\frac {1}{2}$

答案： B 提示:连接DC₁,AC₁.因为四边形ABCD是正方形,且边长为1,所以$AC=\sqrt{2}$,∠DAC=∠OCB₁=45°,∠B=90°.由旋转,得∠CAC₁=45°,∠AB₁C₁=∠B=90°.所以∠CAC₁=∠DAC,CB₁=OB₁,所以点A,D,C₁在一条直线上.易得B₁C₁=AB₁=1,所以$CB₁=OB₁=AC-AB₁=\sqrt{2}-1$.所以阴影部分的面积为$S_{扇形CAC₁}-S_{\triangle OB₁C}-S_{\triangle AB₁C₁}=\frac{45\pi×(\sqrt{2})^{2}}{360}-\frac{1}{2}(\sqrt{2}-1)^{2}-\frac{1}{2}×1×1=\frac{\pi}{4}-2+\sqrt{2}$.

4. 如图,边长为$2\sqrt {2}$的正方形 ABCD 的中心与半径为$2\sqrt {2}的\odot O$的圆心重合,E,F 分别是 AD,BA 的延长线与$\odot O$的交点,则图中阴影部分的面积为 (A)
A.$2π-2\sqrt {3}$
B.$2π-2$
C.$2π+2$
D.$2π+2\sqrt {3}$

答案： A 提示:延长DC,CB,分别交$\odot O$于点M,N,连接OF.由圆与多边形的对称性可知,阴影部分的面积为$\frac{1}{4}(S_{\odot O}-S_{正方形ABCD})-S_{\triangle ADF}$.过点O作OH⊥AB于点H.在Rt△OFH中,由勾股定理,得$FH=\sqrt{OF^{2}-OH^{2}}=\sqrt{6}$.易得$AH=BH=\sqrt{2}$,所以$AF=\sqrt{6}-\sqrt{2}$,所以$S_{\triangle ADF}=\frac{1}{2}AD\cdot AF=2\sqrt{3}-2$.所以阴影部分的面积为$\frac{1}{4}×[\pi×(2\sqrt{2})^{2}-2\sqrt{2}×2\sqrt{2}]-(2\sqrt{3}-2)=2\pi-2\sqrt{3}$.

5. 如图,扇形 OAB 的圆心角是$90^{\circ }$,半径为4 cm,分别以 OA,OB 为直径画半圆,则图中阴影部分的面积为8 cm².

答案： 8 cm²

6. 如图1,一只蚂蚁从圆锥底端点 A 出发,绕圆锥表面爬行一周后回到点 A,将圆锥沿母线 OA 剪开,其侧面展开图如图 2 所示.若$∠AOA'= 120^{\circ },OA= 2\sqrt {3}$,则蚂蚁爬行的最短距离是______6.

答案： 6

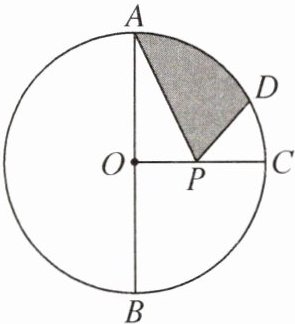
7. 如图,AB 为$\odot O$的直径,且$AB= 2$,OC 是$\odot O$的半径,$OC⊥AB$,点 D 在$\widehat {AC}$上,$\widehat {AD}= 2\widehat {CD}$,P 是 OC 上一动点,则阴影部分周长的最小值为______.

答案： $\sqrt{3}+\frac{\pi}{3}$ 提示:连接OD,AD,PB,BD.因为$\overset{\frown}{AD}=2\overset{\frown}{CD}$,且易得$\overset{\frown}{AC}$的度数是90°,所以$\overset{\frown}{AD}$的度数是60°.所以∠ABD=30°,$\overset{\frown}{AD}$的长为$\frac{60\pi×1}{180}=\frac{\pi}{3}$.所以当PA+PD的值最小时,题图中阴影部分的周长最小.易知B是点A关于OC的对称点,所以PB=PA.所以PA+PD=PB+PD≥BD,所以当P是BD与OC的交点时,PA+PD的值最小,最小值为BD的长.因为AB是$\odot O$的直径,所以∠ADB=90°.易得AD=1,$BD=\sqrt{3}$.所以PA+PD的最小值为$\sqrt{3}$,所以题图中阴影部分周长的最小值为$\sqrt{3}+\frac{\pi}{3}$.