9. 如图,在平面直角坐标系中,点 A 的坐标为 $ (2,0) $,点 B 的坐标为 $ (6,0) $,点 C 的坐标为 $ (0,8) $,D 为平面上一动点,CD 的长度为 a,Q 为 BD 的中点,当点 D 运动时,所有这样的点 Q 组成的图形与线段 AB 有且只有一个公共点,则 a 的取值应满足的条件是______
a=8或2$\sqrt{17}$<a≤10
.
答案:
a=8或2$\sqrt{17}$<a≤10 提示:由条件知,点D在以点C为圆心,a为半径的圆上,连接BC,取其中点M,则点M的坐标为(3,4).连接MQ,则MQ为△BCD的中位线,所以MQ//CD,且MQ=$\frac{1}{2}$CD=$\frac{1}{2}$a,从而点Q组成的图形是以点M(3,4)为圆心,$\frac{1}{2}$a为半径的圆.当点Q组成的图形与线段AB有且只有一个公共点时,可得$\frac{1}{2}$a=4,即a=8符合题意(此时圆与AB相切).又因为MA=$\sqrt{(3−2)²+4²}$=$\sqrt{17}$,MB=$\sqrt{(3−6)²+4²}$=5,所以当$\sqrt{17}$<$\frac{1}{2}$a≤5,即2$\sqrt{17}$<a≤10时,也符合题意.综上所述,a=8或2$\sqrt{17}$<a≤10.
10. 已知 P 为图形 M 上任意一点,Q 为图形 N 上任意一点,如果 P,Q 两点间的距离有最小值,那么称这个最小值为图形 M,N 间的“距离”,记作 $ d(M,N) $. 特别地,若图形 M,N 有公共点,规定 $ d(M,N)= 0 $.
(1)如图 1,$ \odot O $ 的半径为 2.
①已知点 $ A(0,1) $,$ B(4,3) $,则 $ d(A,\odot O)= $______,$ d(B,\odot O)= $______;
②已知直线 $ l:y= -\frac{5}{12}x+b $ 与 $ \odot O $ 的“距离”$ d(l,\odot O)= \frac{34}{13} $,求 b 的值.
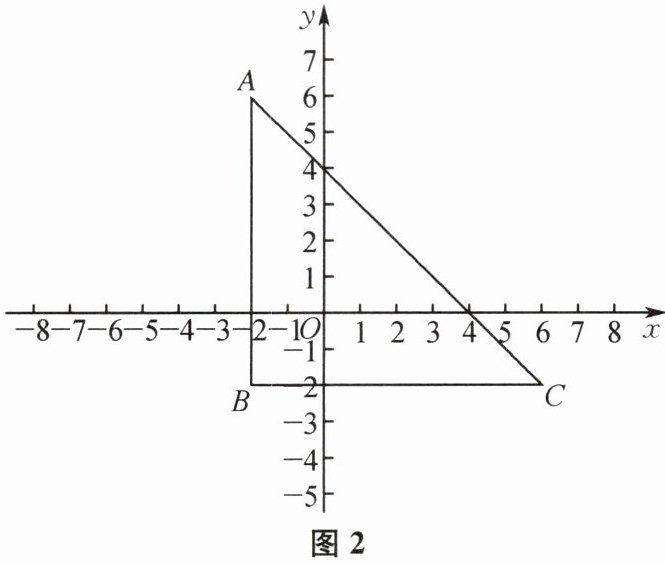
(2)如图 2,已知点 $ A(-2,6) $,$ B(-2,-2) $,$ C(6,-2) $,$ \odot M $ 的圆心为 $ M(m,0) $,半径为 1. 若 $ d(\odot M,\triangle ABC)= 1 $,求 m 的取值范围.
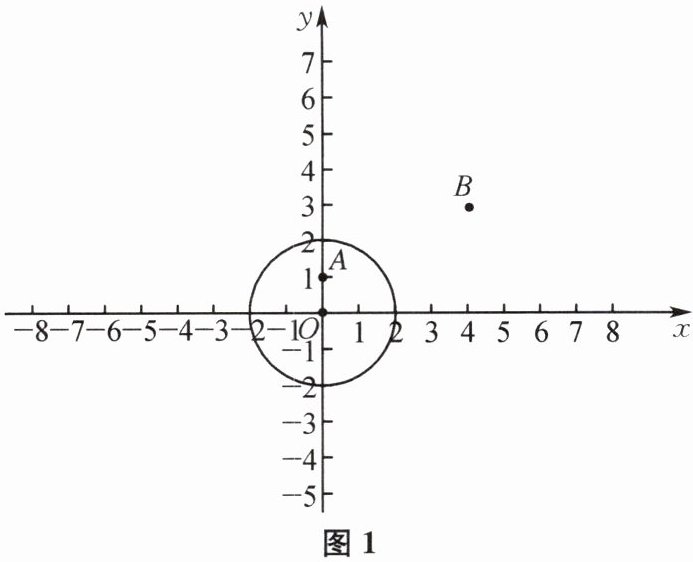
(1)如图 1,$ \odot O $ 的半径为 2.
①已知点 $ A(0,1) $,$ B(4,3) $,则 $ d(A,\odot O)= $______,$ d(B,\odot O)= $______;
②已知直线 $ l:y= -\frac{5}{12}x+b $ 与 $ \odot O $ 的“距离”$ d(l,\odot O)= \frac{34}{13} $,求 b 的值.
(2)如图 2,已知点 $ A(-2,6) $,$ B(-2,-2) $,$ C(6,-2) $,$ \odot M $ 的圆心为 $ M(m,0) $,半径为 1. 若 $ d(\odot M,\triangle ABC)= 1 $,求 m 的取值范围.


答案:
解:
(1)①1 3
②设直线l分别交x轴、y轴于点P,Q,过点O作OH⊥PQ于点H,OH交⊙O于点G.由题意可知,点P($\frac{12}{5}$b,0),Q(0,b),所以OP=$\frac{12}{5}$|b|,OQ=|b|,所以由勾股定理,得PQ=$\frac{13}{5}$|b|.因为S△POQ=$\frac{1}{2}$OP·OQ=$\frac{1}{2}$PQ·OH,所以OH=$\frac{12}{13}$|b|.又因为直线l:y=−$\frac{5}{12}$x+b与⊙O的“距离”d(l,⊙O)=$\frac{34}{13}$,所以$\frac{12}{13}$|b|−2=$\frac{34}{13}$,所以b=±5.
(2)如图,设AC交x轴于点E,则易得点E(4,0).因为d(⊙M,△ABC)=1,所以当m=−4时,⊙M₁满足条件;当m=0时,⊙M₂恰好满足条件.假设⊙M₃恰好满足条件,过点M₃作M₃H⊥AC于点H,则M₃H=2.由条件易知,HE=HM₃=2,所以EM₃=2$\sqrt{2}$,所以点M₃(4−2$\sqrt{2}$,0),所以m=4−2$\sqrt{2}$.观察图形可知,当0≤m≤4−2$\sqrt{2}$时,⊙M始终满足条件.假设⊙M₄恰好满足条件,过点M₄作M₄G⊥AC于点G,则M₄G=2.由条件易知,GE=GM₄=2,所以EM₄=2$\sqrt{2}$,所以点M₄(4+2$\sqrt{2}$,0),所以m=4+2$\sqrt{2}$.综上所述,满足条件的m的取值范围是m=−4或0≤m≤4−2$\sqrt{2}$或m=4+2$\sqrt{2}$.

解:
(1)①1 3
②设直线l分别交x轴、y轴于点P,Q,过点O作OH⊥PQ于点H,OH交⊙O于点G.由题意可知,点P($\frac{12}{5}$b,0),Q(0,b),所以OP=$\frac{12}{5}$|b|,OQ=|b|,所以由勾股定理,得PQ=$\frac{13}{5}$|b|.因为S△POQ=$\frac{1}{2}$OP·OQ=$\frac{1}{2}$PQ·OH,所以OH=$\frac{12}{13}$|b|.又因为直线l:y=−$\frac{5}{12}$x+b与⊙O的“距离”d(l,⊙O)=$\frac{34}{13}$,所以$\frac{12}{13}$|b|−2=$\frac{34}{13}$,所以b=±5.
(2)如图,设AC交x轴于点E,则易得点E(4,0).因为d(⊙M,△ABC)=1,所以当m=−4时,⊙M₁满足条件;当m=0时,⊙M₂恰好满足条件.假设⊙M₃恰好满足条件,过点M₃作M₃H⊥AC于点H,则M₃H=2.由条件易知,HE=HM₃=2,所以EM₃=2$\sqrt{2}$,所以点M₃(4−2$\sqrt{2}$,0),所以m=4−2$\sqrt{2}$.观察图形可知,当0≤m≤4−2$\sqrt{2}$时,⊙M始终满足条件.假设⊙M₄恰好满足条件,过点M₄作M₄G⊥AC于点G,则M₄G=2.由条件易知,GE=GM₄=2,所以EM₄=2$\sqrt{2}$,所以点M₄(4+2$\sqrt{2}$,0),所以m=4+2$\sqrt{2}$.综上所述,满足条件的m的取值范围是m=−4或0≤m≤4−2$\sqrt{2}$或m=4+2$\sqrt{2}$.

查看更多完整答案,请扫码查看


