《2025年小题狂做九年级数学上册苏科版巅峰版》

1. 某商店购进一种商品,进价为30元/件.试销期间发现这种商品每天的销售量P(件)与每件的销售价x(元)满足关系：P= 100-2x.若商店在试销期间每天销售这种商品获得200元的利润,则下面所列方程正确的是(A)
A.(x-30)(100-2x)= 200
B.x(100-2x)= 200
C.(30-x)(100-2x)= 200
D.(x-30)(2x-100)= 200

答案： A

2. 已知实数m使关于x的反比例函数y= $\frac{m-3}{x}$的图像在第二、四象限,且使关于x的方程2(m-2)x^2-2(2m-1)x+2m+1= 0有实数根.若m是整数,则所有满足条件的m的值的和为(C)
A.-2
B.-1
C.0
D.1

答案： C 提示:因为反比例函数$ y=\frac{m-3}{x} $的图像在第二、四象限,所以$ m-3＜0 $,解得$ m＜3 $.关于x的方程$ 2(m-2)x^{2}-2(2m-1)x+2m+1=0 $有实数根,当方程是一元一次方程时,$ m=2 $,有实数根;当方程是一元二次方程时,$ 2(m-2)\neq0 $,$ m\neq2 $,$ [-2(2m-1)]^{2}-4×2(m-2)×(2m+1)\geq0 $,解得$ m\geq-\frac{5}{2} $.综上所述,m可取的整数值有-2,-1,0,1,2,它们的和为0.

3. 如图,将图1的正方形剪成四块,且这四块恰能无缝隙、不重叠地拼成图2的矩形,设a= 1,则b的值为(B)
A.$\frac{\sqrt{5}-1}{2}$
B.$\frac{\sqrt{5}+1}{2}$
C.$\frac{\sqrt{5}+3}{2}$
D.$\sqrt{2}+1$

答案： B 提示:根据题意,得$ (a+b)^{2}=b(a+2b) $.因为$ a=1 $,所以$ (1+b)^{2}=b(1+2b) $.整理,得$ b^{2}-b-1=0 $,解得$ b=\frac{\sqrt{5}+1}{2} $(负值已舍).

4. 若关于x的方程$x^2-ax+2a= 0$的两个实数根的平方和是5,则a的值是(D)
A.-1或5
B.1
C.5
D.-1

答案： D 提示:设两根分别为$ x_{1},x_{2} $,则$ x_{1}^{2}+x_{2}^{2}=5 $.所以$ (x_{1}+x_{2})^{2}-2x_{1}x_{2}=a^{2}-2×2a=5 $.整理,得$ a^{2}-4a-5=0 $,解得$ a_{1}=5 $,$ a_{2}=-1 $.当$ a=5 $时,原方程无实数根;当$ a=-1 $时,方程有两个不相等的实数根.所以$ a=-1 $.

5. (泰州市姜堰区模拟)若一个一元二次方程的两个根分别是Rt△ABC的两条直角边的长,且$S_{\triangle ABC}= 3$,请写出一个符合题意的一元二次方程：______$ x^{2}-7x+6=0 $.

答案： $ x^{2}-7x+6=0 $(答案不唯一)

6. 若关于x的方程$kx^2-4x+3= 0$有实数根,则k的非负整数值是0或1.

答案： 0或1

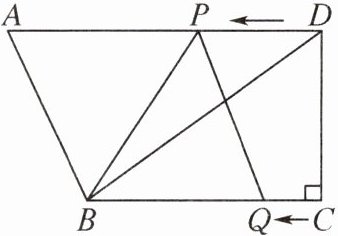
7. 如图,在四边形ABCD中,AD//BC,∠C= 90°,BC= 8,DC= 6,AD= 14.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t s,当t= ______时,以B,P,Q三点为顶点的三角形是等腰三角形.

答案：
$ \frac{7}{4} $或$ \frac{8}{3} $ 提示:如图,过点P作$ PM\perp BC $于点M,则四边形PDCM为矩形.由图可知,$ CM=PD=2t $,$ PM=DC=6 $,$ CQ=t $,所以$ QM=t $,$ BQ=8-t $,$ BM=|8-2t| $.若以B,P,Q为顶点的三角形是等腰三角形,则$ 0＜t＜8 $,且可以分三种情况:①若$ PQ=BQ $,在$ Rt\triangle PQM $中,$ PQ^{2}=t^{2}+6^{2} $,由$ PQ^{2}=BQ^{2} $,得$ t^{2}+6^{2}=(8-t)^{2} $,解得$ t=\frac{7}{4} $.②若$ BP=BQ $,在$ Rt\triangle PMB $中,$ PB^{2}=(8-2t)^{2}+6^{2} $,由$ PB^{2}=BQ^{2} $,得$ (8-2t)^{2}+6^{2}=(8-t)^{2} $,即$ 3t^{2}-16t+36=0 $,此时$ (-16)^{2}-4×3×36＜0 $,所以此方程无解,所以$ BP\neq BQ $.③若$ PB=PQ $,则$ BM=MQ $,即$ 8-2t=t $,解得$ t=\frac{8}{3} $.综上所述,当$ t=\frac{7}{4} $或$ t=\frac{8}{3} $时,以B,P,Q三点为顶点的三角形是等腰三角形.

8. 已知实数m,n满足$m^2-am+1= 0,n^2-an+1= 0,$且m≠n.若a≥3,则代数式$(m-1)^2+(n-1)^2$的最小值是______3.

答案： 3 提示:由题意,得$ m^{2}+1=am $,$ n^{2}+1=an $,且m,n可看作关于x的一元二次方程$ x^{2}-ax+1=0 $的两根,所以$ m+n=a $,$ (-a)^{2}-4×1×1＞0 $,即$ a＞2 $或$ a＜-2 $.所以$ (m-1)^{2}+(n-1)^{2}=m^{2}-2m+1+n^{2}-2n+1=am+an-2m-2n=a(m+n)-2(m+n)=(a-2)(m+n)=a(a-2)=a^{2}-2a=(a-1)^{2}-1 $.因为$ a\geq3 $,所以当$ a=3 $时,$ (m-1)^{2}+(n-1)^{2} $有最小值,且最小值为$ (3-1)^{2}-1=3 $.

9. 定义新运算“★”如下：当a≥b时,a★b= ab+b；当a＜b时,a★b= ab-3(a-9).若(2x-1)★(x+2)= 48,则x的值为4或$ -\frac{5}{2} $.

答案： 4或$ -\frac{5}{2} $ 提示:当$ 2x-1\geq x+2 $,即$ x\geq3 $时,根据题意,得$ (2x-1)(x+2)+(x+2)=48 $,解得$ x_{1}=4 $,$ x_{2}=-6 $(舍去);当$ 2x-1＜x+2 $,即$ x＜3 $时,根据题意,得$ (2x-1)(x+2)-3[(2x-1)-9]=48 $,解得$ x_{1}=-\frac{5}{2} $,$ x_{2}=4 $(舍去).综上所述,x的值为4或$ -\frac{5}{2} $.

10. 某电解金属锰厂从今年1月起安装使用回收净化设备(安装时间不计),这样既改善了环境,又降低了原料成本.据统计,在使用回收净化设备后的1至x个月的月利润平均值w(万元)满足w= 10x+90,则前9个月的利润和等于1620万元.

答案： 9 提示:根据题意,得$ x(10x+90)=1620 $,解得$ x_{1}=9 $,$ x_{2}=-18 $(舍去).所以前9个月的利润和等于1620万元.

11. 已知关于x的方程$x^2+(a-6)x+a= 0$的两个根都是整数,则a的值为0或16.

答案： 0或16 提示:设这两个根分别为$ x_{1} $,$ x_{2}(x_{1}\geq x_{2}) $,则$ x_{1}x_{2}+x_{1}+x_{2}=6 $,即$ (x_{1}+1)(x_{2}+1)=7 $.因为$ x_{1} $,$ x_{2} $都是整数,$ x_{1}\geq x_{2} $,所以$ \left\{\begin{array}{l} x_{1}+1=7,\\ x_{2}+1=1\end{array}\right. $或$ \left\{\begin{array}{l} x_{1}+1=-1,\\ x_{2}+1=-7,\end{array}\right. $所以$ \left\{\begin{array}{l} x_{1}=6,\\ x_{2}=0\end{array}\right. $或$ \left\{\begin{array}{l} x_{1}=-2,\\ x_{2}=-8.\end{array}\right. $所以$ a=x_{1}x_{2}=0 $或$ a=x_{1}x_{2}=16 $.