《2025年小题狂做九年级数学上册苏科版巅峰版》

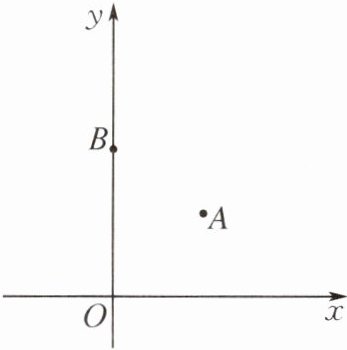
1. 如图,在平面直角坐标系中,点 A(3,3),B(0,5).若在坐标轴上取点 C,使△ABC 为等腰三角形,则满足条件的点 C 的个数是(D)

A.3
B.4
C.5
D.7

答案： D 提示:当AC=CB时，作AB的垂直平分线，交x轴、y轴共有两个点C;当AB=AC时,以点A为圆心，AB为半径作⊙A，交y轴、x轴共有三个点C;当AB=BC时，以点B为圆心,AB为半径作⊙B,交y轴有两个点C.由作图可得，一共有7个满足条件的点C.

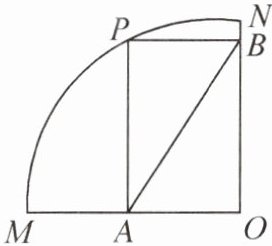
2. 如图,四边形 PAOB 是扇形 OMN 的内接矩形,顶点 P 在$\overset{\frown}{MN}$上,且不与点 M,N 重合.当点 P 在$\overset{\frown}{MN}$上移动时,矩形 PAOB 的形状、大小随之变化,其中$PA^{2}+PB^{2}$的值的变化情况是(A)

A.不变
B.逐渐变小
C.逐渐变大
D.不能确定

答案： A 提示:连接OP.由题意可知，$PA^{2}+PB^{2}=AB^{2}=OP^{2}$，所以$PA^{2}+PB^{2}$的值不变.

3. 如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(网格线的交点称为格点).现以点 A 为圆心,r 为半径画圆,如果选取的格点中除点 A 外恰好有3个在圆内,那么 r 的取值范围是(B)
A.$2\sqrt{2}＜r\leq\sqrt{17}$
B.$\sqrt{17}＜r\leq3\sqrt{2}$
C.$\sqrt{17}＜r\leq5$
D.$5＜r\leq\sqrt{29}$

答案： B 提示:分别计算除点A外的8个格点到点A的距离，并按距离的值从小到大的顺序排序为$2\sqrt {2},\sqrt {17},\sqrt {17},3\sqrt {2},5,5,5,\sqrt {29}$，所以距离为$2\sqrt {2},\sqrt {17},\sqrt {17}$的3个点在圆内,其余的点在圆上或圆外，所以$\sqrt {17}＜r＜3\sqrt {2}$

4. 如图,在矩形 ABCD 中,AB= 2,BC= 3,以点 A 为圆心,1 为半径画圆,E 是$\odot A$上一动点,P 是 BC 上一动点,则 PE+PD 的最小值为(C)
A.2
B.3
C.4
D.$2\sqrt{3}$

答案： C 提示:过点D作关于直线BC的对称点F，连接AF，交BC于点P，交⊙A于点E，此时$PE+PD$的值最小，为EF的长.因为四边形ABCD是矩形，所以$∠ADF=90^{\circ },AB=CD=2,AD=BC=3$，所以DF=4.由勾股定理，得$AF=\sqrt {AD^{2}+DF^{2}}=5$，所以$AE+EF=5$，所以$EF=5 - 1=4$，所以$PE+PD$的最小值为4.

5. (扬州市邗江区期末)已知$\odot O$的半径为5,圆心在坐标原点,位于第二象限的该圆上的一点 P 的横坐标和纵坐标均为整数,则点 P 的坐标为(-3,4)或(-4,3).

答案： (-3,4)或(-4,3)

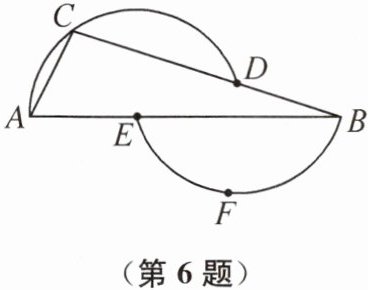
6. 如图,过 D,A,C 三点的圆的圆心为点 E,过 B,E,F 三点的圆的圆心为点 D.如果∠A= 63°,那么∠B= ______.

18°

答案： $18^{\circ }$ 提示:连接CE,DE,则$AE=CE=DE=BD$，所以$∠ACE=∠A=63^{\circ },∠DEB=∠B$.易得$∠ECD=∠CDE=∠DEB+∠B=2∠B$，所以$∠AEC=∠ECD+∠B=3∠B$.因为$∠A+∠ACE+∠AEC=180^{\circ }$，所以$63^{\circ }+63^{\circ }+3∠B=180^{\circ }$，所以$∠B=18^{\circ }$

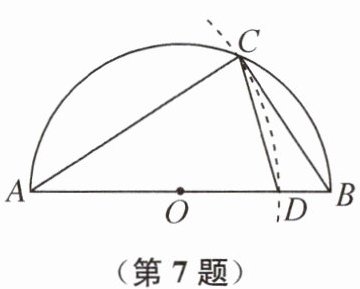
7. 如图,以 AB 为直径的半圆 O 经过点 C,以点 A 为圆心,AC 为半径画弧交 AB 于点 D,连接 CD.若$CD= \frac{1}{2}AB$,则∠BCD 的度数为______$18^{\circ }$.

答案： $18^{\circ }$ 提示:如图，连接OC，则$OC=\frac {1}{2}AB=CD$，所以$∠COD=∠CDO$.设$∠A=x$，因为$OA=OC,AC=AD$，所以$∠OCA=x,∠ACD=∠CDO=∠COD=2x$，所以在$\triangle ACD$中，$x+2x+2x=180^{\circ }$，解得$x=36^{\circ }$，即$∠COD=∠CDO=2x=72^{\circ }$，所以$∠OCD=36^{\circ }$.因为$OC=OB$，所以$∠OCB=∠B=\frac {180^{\circ }-72^{\circ }}{2}=54^{\circ }$，所以$∠BCD=∠OCB-∠OCD=18^{\circ }$

8. 在平面直角坐标系中,已知点 A(3,0),B 是以点 M(3,4)为圆心,1 为半径的圆上一动点,连接 OB.设 OB 的中点为 C,则线段 AC 长的最小值为______2.

答案： 2 提示:如图，在x轴上截取$AD=OA$，连接DB,MB,DM.易知AC是$\triangle ODB$的中位线，所以$AC=\frac {1}{2}DB$，所以当线段DB的长最短时，线段AC的长最短.因为$DB≥DM-MB=DM-1$，所以当点D,B,M依次共线时，线段DB的长最短.因为点A(3,0)，所以点D(6,0)，所以$DM=\sqrt {(6 - 3)^{2}+(0 - 4)^{2}}=5$，此时$DB=5 - 1=4$.所以线段AC长的最小值为2.