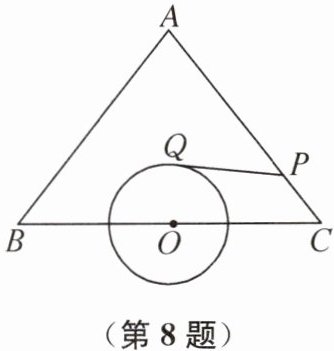
8. 如图,在等腰三角形ABC中,AB= AC= 5,BC= 6,O是边BC的中点,⊙O的半径为1,P是边AC上一动点,则由点P出发到⊙O的切线长PQ的最小值为______.

答案:
√119/5 提示:连接OP,OQ,AO,则OQ⊥PQ.在Rt△OPQ中,PQ=√(OP²−OQ²)=√(OP²−1),所以当OP的长最短时,PQ的值最小.当OP⊥AC时,OP的长最短.因为AB=AC=5,BC=6,O是边BC的中点,所以AO⊥BC,OC=1/2BC=3,所以AO=√(AC²−OC²)=4.此时S△AOC=1/2×5×OP=1/2×3×4,所以OP=12/5.所以PQ=√(OP²−1)=√119/5,即切线长PQ的最小值为√119/5.
9. 如图,已知线段AM= 5,射线AS垂直于AM,点N在射线AS上,设AN= n,点P在经过点N且平行于AM的直线上运动,∠PAM的平分线交直线NP于点Q,过点Q作QB//AP,交线段AM于点B,连接PB交AQ于点C,以点Q为圆心,QC为半径作圆.
(1)判断PB与⊙Q的位置关系为_____
(2)已知⊙Q的半径为3,当AM所在直线与⊙Q相切时,求PA的长.
(1)判断PB与⊙Q的位置关系为_____
相切
.(2)已知⊙Q的半径为3,当AM所在直线与⊙Q相切时,求PA的长.
2√3
答案:
(1)相切 提示:因为QB//PA,PQ//AB,所以四边形APQB为平行四边形.因为∠PAM的平分线交直线NP于点Q,所以∠PAQ=∠BAQ.又因为PQ//AB,所以∠PQA=∠BAQ.所以∠PAQ=∠PQA,所以PA=PQ.所以四边形APQB为菱形.所以PB⊥AQ,垂足为C,所以PB与⊙Q相切.
(2)如图,当AM与⊙Q相切于点D时,连接QD,可知AN=QD=QC=3,AQ=6,∠ADQ=90°.在Rt△ADQ中,AD=√(AQ²−DQ²)=3√3.由
(1)知,四边形APQB为菱形,故可设PA=AB=BQ=x,则BD=3√3−x.在Rt△BDQ中,BD²+QD²=BQ²,即(3√3−x)²+3²=x²,解得x=2√3,即PA=2√3.
(1)相切 提示:因为QB//PA,PQ//AB,所以四边形APQB为平行四边形.因为∠PAM的平分线交直线NP于点Q,所以∠PAQ=∠BAQ.又因为PQ//AB,所以∠PQA=∠BAQ.所以∠PAQ=∠PQA,所以PA=PQ.所以四边形APQB为菱形.所以PB⊥AQ,垂足为C,所以PB与⊙Q相切.
(2)如图,当AM与⊙Q相切于点D时,连接QD,可知AN=QD=QC=3,AQ=6,∠ADQ=90°.在Rt△ADQ中,AD=√(AQ²−DQ²)=3√3.由
(1)知,四边形APQB为菱形,故可设PA=AB=BQ=x,则BD=3√3−x.在Rt△BDQ中,BD²+QD²=BQ²,即(3√3−x)²+3²=x²,解得x=2√3,即PA=2√3.
10. 如图,在平面直角坐标系中,y轴的正半轴(坐标原点除外)上有两点A(0,3),B(0,7),C为x轴的正半轴(坐标原点除外)上一动点.当∠ACB取最大值时,点C的横坐标为 (
A.5
B.2
C.21
D.$\sqrt{21}$
D
)A.5
B.2
C.21
D.$\sqrt{21}$
答案:
D 提示:如图,当△ABC的外接圆⊙M与x轴正半轴相切于点C时,∠AMB最大.因为∠ACB=1/2∠AMB,所以此时∠ACB最大.过点M作MD⊥y轴于点D,连接MC,MB,MA.易知AD=BD=1/2AB=2,CM⊥x轴,所以OD=MC=MB=OA+AD=3+2=5.在Rt△BMD中,MD=√(MB²−BD²)=√21.所以OC=MD=√21,所以点C的横坐标为√21.
11. 如图1,在四边形ABCD中,∠BAD= ∠D= 90°,AD= 8,CD= 6,AB= m.过A,B,C三点的⊙O的圆心位置和半径随着m的变化而变化.
【特殊情形】
(1)如图2,当m= 0,且圆心O在AD上时,求⊙O的半径.
【一般情形】
(2)当m= 2时,求⊙O的半径.
(3)当m>0时,随着m的增大,点O的运动路径是
①射线;②弧;③双曲线的一部分;④不规则的曲线.
【深入研究】
(4)如图3,连接AC,以点O为圆心,作出与边CD相切的圆,记为小⊙O.当小⊙O与AC相交且与BC相离时,直接写出m的取值范围.
【特殊情形】
(1)如图2,当m= 0,且圆心O在AD上时,求⊙O的半径.
【一般情形】
(2)当m= 2时,求⊙O的半径.
(3)当m>0时,随着m的增大,点O的运动路径是
①
(填序号).①射线;②弧;③双曲线的一部分;④不规则的曲线.
【深入研究】
(4)如图3,连接AC,以点O为圆心,作出与边CD相切的圆,记为小⊙O.当小⊙O与AC相交且与BC相离时,直接写出m的取值范围.
(1)解:设⊙O半径为r,圆心O在AD上,坐标为(0,8-r)。
当m=0时,A、B重合,A(0,0),C(6,8)。
OA=r,OC=r,
则$\sqrt{(6-0)^2+(8-(8-r))^2}=r$,
即$\sqrt{36+r^2}=r$,解得$r=\frac{13}{4}$。
当m=0时,A、B重合,A(0,0),C(6,8)。
OA=r,OC=r,
则$\sqrt{(6-0)^2+(8-(8-r))^2}=r$,
即$\sqrt{36+r^2}=r$,解得$r=\frac{13}{4}$。
(2)解:建立坐标系,A(0,0),B(m,0)=(2,0),C(6,8)。
圆心O(x,y),OA=OB=OC,
由OA=OB得$x^2+y^2=(x-2)^2+y^2$,解得x=1。
由OA=OC得$1^2+y^2=(6-1)^2+(8-y)^2$,
即$1+y^2=25+(8-y)^2$,解得$y=\frac{41}{8}$。
半径$OA=\sqrt{1^2+(\frac{41}{8})^2}=\frac{\sqrt{1745}}{8}$。
圆心O(x,y),OA=OB=OC,
由OA=OB得$x^2+y^2=(x-2)^2+y^2$,解得x=1。
由OA=OC得$1^2+y^2=(6-1)^2+(8-y)^2$,
即$1+y^2=25+(8-y)^2$,解得$y=\frac{41}{8}$。
半径$OA=\sqrt{1^2+(\frac{41}{8})^2}=\frac{\sqrt{1745}}{8}$。
(4)$\frac{14}{3} < m < \frac{26}{3}$
答案:
(1)解:设⊙O半径为r,圆心O在AD上,坐标为(0,8-r)。
当m=0时,A、B重合,A(0,0),C(6,8)。
OA=r,OC=r,
则$\sqrt{(6-0)^2+(8-(8-r))^2}=r$,
即$\sqrt{36+r^2}=r$,解得$r=\frac{13}{4}$。
(2)解:建立坐标系,A(0,0),B(m,0)=(2,0),C(6,8)。
圆心O(x,y),OA=OB=OC,
由OA=OB得$x^2+y^2=(x-2)^2+y^2$,解得x=1。
由OA=OC得$1^2+y^2=(6-1)^2+(8-y)^2$,
即$1+y^2=25+(8-y)^2$,解得$y=\frac{41}{8}$。
半径$OA=\sqrt{1^2+(\frac{41}{8})^2}=\frac{\sqrt{1745}}{8}$。
(3)①
(4)$\frac{14}{3} < m < \frac{26}{3}$
当m=0时,A、B重合,A(0,0),C(6,8)。
OA=r,OC=r,
则$\sqrt{(6-0)^2+(8-(8-r))^2}=r$,
即$\sqrt{36+r^2}=r$,解得$r=\frac{13}{4}$。
(2)解:建立坐标系,A(0,0),B(m,0)=(2,0),C(6,8)。
圆心O(x,y),OA=OB=OC,
由OA=OB得$x^2+y^2=(x-2)^2+y^2$,解得x=1。
由OA=OC得$1^2+y^2=(6-1)^2+(8-y)^2$,
即$1+y^2=25+(8-y)^2$,解得$y=\frac{41}{8}$。
半径$OA=\sqrt{1^2+(\frac{41}{8})^2}=\frac{\sqrt{1745}}{8}$。
(3)①
(4)$\frac{14}{3} < m < \frac{26}{3}$
查看更多完整答案,请扫码查看


