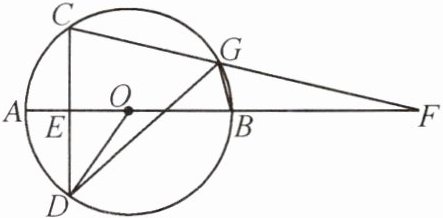
10. 如图,AB是⊙O的直径,弦CD⊥AB于点E,G为劣弧BC上一动点,CG与AB的延长线交于点F,连接OD,DG,GB.
(1)试判断∠AOD与∠CGD的大小关系,并说明:GB平分∠DGF.
(2)在点G的运动过程中,当GD= GF时,若DE= 4,BF= 4√5,求⊙O的半径.
(1)试判断∠AOD与∠CGD的大小关系,并说明:GB平分∠DGF.
(2)在点G的运动过程中,当GD= GF时,若DE= 4,BF= 4√5,求⊙O的半径.

答案:
解:
(1) ∠AOD = ∠CGD.理由如下:连接 OC,BC,BD.因为 AB 是⊙O 的直径,弦 CD⊥AB,所以∠AOD = 1/2∠COD = ∠CGD,⌢BD = ⌢BC,所以∠BCD = ∠BGD = ∠BDC.因为四边形 BDCG 为⊙O 的内接四边形,所以∠BGC + ∠BDC = 180°.又因为∠BGC + ∠BGF = 180°,所以∠BGF = ∠BDC.所以∠BGD = ∠BGF,即 GB 平分∠DGF.
(2) 根据题意,易证△BGD ≌ △BGF,所以 BD = BF = 4√5,所以 BE = √(BD² - DE²) = 8.设⊙O 的半径为 r,则 OD = r,OE = BE - OB = 8 - r.在 Rt△ODE 中,由勾股定理,得 OE² + DE² = OD²,即(8 - r)² + 4² = r²,解得 r = 5.所以⊙O 的半径为 5.
(1) ∠AOD = ∠CGD.理由如下:连接 OC,BC,BD.因为 AB 是⊙O 的直径,弦 CD⊥AB,所以∠AOD = 1/2∠COD = ∠CGD,⌢BD = ⌢BC,所以∠BCD = ∠BGD = ∠BDC.因为四边形 BDCG 为⊙O 的内接四边形,所以∠BGC + ∠BDC = 180°.又因为∠BGC + ∠BGF = 180°,所以∠BGF = ∠BDC.所以∠BGD = ∠BGF,即 GB 平分∠DGF.
(2) 根据题意,易证△BGD ≌ △BGF,所以 BD = BF = 4√5,所以 BE = √(BD² - DE²) = 8.设⊙O 的半径为 r,则 OD = r,OE = BE - OB = 8 - r.在 Rt△ODE 中,由勾股定理,得 OE² + DE² = OD²,即(8 - r)² + 4² = r²,解得 r = 5.所以⊙O 的半径为 5.
11. 如图,在△ABC中,AC= 4√3,BC= 9,∠ACB= 60°,AM//BC,点P在射线AM上运动,连接BP交△APC的外接圆于点E,则AE长的最小值为______
2√3
.
答案:
2√3 提示:如图,连接 CE.因为 AM//BC,所以∠MAC = ∠ACB = 60°,所以∠CEP = ∠MAC = 60°,所以∠BEC = 120°.因为 BC = 9,所以点 E 在所对弦 BC = 9,含圆周角∠BEC = 120°的劣弧 BC 上运动.设该劣弧所在的圆心为点 O,连接 OB,OC,OA,OA 交⊙O 于点 E',延长 AO 交⊙O 于另一点 G,连接 BG,CG,过点 O 作 OH⊥BC 于点 H.易证 AE'的长为 AE 长的最小值.易知∠BEC + ∠BGC = 180°,所以∠BGC = 60°,所以∠BOC = 120°.又因为 OB = OC,OH⊥BC,所以 BH = CH = 1/2BC = 9/2,∠OBH = ∠OCH = 30°,所以 OB = 2OH.在 Rt△OHB 中,由勾股定理,得 OH² + BH² = OB²,即 OH² + (9/2)² = (2OH)²,解得 OH = 3√3/2(负值已舍).所以 OE' = OC = OB = 2OH = 3√3.因为∠ACB = 60°,∠OCB = 30°,所以∠ACO = 90°.所以 OA = √(OC² + AC²) = 5√3.所以 AE' = OA - OE' = 2√3,即 AE 长的最小值为 2√3.
12. (1)证明定理:圆内接四边形的对角互补.
已知:如图1,四边形ABCD内接于⊙O.
求证:∠A+∠C= ∠B+∠D= 180°.
(2)逆命题证明:如图2,若四边形的一组对角∠A+∠C= 180°,则这个四边形的4个顶点共圆.可以用反证法证明如下:
在图2中,经过点A,B,D画⊙O.
假设点C落在⊙O外,BC交⊙O于点E,连接DE.
因为四边形ABED内接于⊙O,所以
(3)结论运用:如图3,∠BAC= 120°,AB的长为8/3,点D,E分别在射线AC和线段AB上运动,以DE为边在∠BAC内部作等边三角形DEF,则BF长的最小值为
已知:如图1,四边形ABCD内接于⊙O.
求证:∠A+∠C= ∠B+∠D= 180°.
证明:如图,连接 OB,OD.因为∠A = 1/2∠2,∠C = 1/2∠1,且∠1 + ∠2 = 360°,所以∠A + ∠C = 1/2∠1 + 1/2∠2 = 180°.同理∠ABC + ∠ADC = 180°.所以∠A + ∠C = ∠ABC + ∠ADC = 180°.
(2)逆命题证明:如图2,若四边形的一组对角∠A+∠C= 180°,则这个四边形的4个顶点共圆.可以用反证法证明如下:
在图2中,经过点A,B,D画⊙O.
假设点C落在⊙O外,BC交⊙O于点E,连接DE.
因为四边形ABED内接于⊙O,所以
∠A + ∠BED
= 180°.因为∠A+∠C= 180°,所以∠BED=∠C
,与∠BED>∠C矛盾.同理,点C也不会落在⊙O内,所以A,B,C,D四点共圆.(3)结论运用:如图3,∠BAC= 120°,AB的长为8/3,点D,E分别在射线AC和线段AB上运动,以DE为边在∠BAC内部作等边三角形DEF,则BF长的最小值为
4√3/3
.
答案:
(1) 证明:如图,连接 OB,OD.因为∠A = 1/2∠2,∠C = 1/2∠1,且∠1 + ∠2 = 360°,所以∠A + ∠C = 1/2∠1 + 1/2∠2 = 180°.同理∠ABC + ∠ADC = 180°.所以∠A + ∠C = ∠ABC + ∠ADC = 180°.
(2) ∠A + ∠BED ∠C
(3) 4√3/3 提示:因为△DEF 是等边三角形,所以∠EDF = ∠EFD = 60°.因为∠BAC = 120°,所以∠BAC + ∠EFD = 180°,所以 A,D,F,E 四点共圆.连接 AF,则∠BAF = ∠EDF = 60°.在∠BAC 内部作∠BAM = 60°,则点 F 始终在射线 AM 上运动.由垂线段最短可知,当 BF⊥AM 时,BF 的长最小.此时,在 Rt△ABF 中,∠ABF = 30°,所以 AF = 1/2AB = 4/3,所以 BF = √(AB² - AF²) = 4√3/3,即 BF 长的最小值为 4√3/3.
(1) 证明:如图,连接 OB,OD.因为∠A = 1/2∠2,∠C = 1/2∠1,且∠1 + ∠2 = 360°,所以∠A + ∠C = 1/2∠1 + 1/2∠2 = 180°.同理∠ABC + ∠ADC = 180°.所以∠A + ∠C = ∠ABC + ∠ADC = 180°.
(2) ∠A + ∠BED ∠C
(3) 4√3/3 提示:因为△DEF 是等边三角形,所以∠EDF = ∠EFD = 60°.因为∠BAC = 120°,所以∠BAC + ∠EFD = 180°,所以 A,D,F,E 四点共圆.连接 AF,则∠BAF = ∠EDF = 60°.在∠BAC 内部作∠BAM = 60°,则点 F 始终在射线 AM 上运动.由垂线段最短可知,当 BF⊥AM 时,BF 的长最小.此时,在 Rt△ABF 中,∠ABF = 30°,所以 AF = 1/2AB = 4/3,所以 BF = √(AB² - AF²) = 4√3/3,即 BF 长的最小值为 4√3/3.
查看更多完整答案,请扫码查看


