8. 如图,以 AB 为边作边长为8的正方形 ABCD,动点 P,Q 在正方形 ABCD 的边上运动,且$PQ= 8$.若点 P 从点 A 出发,沿$A→B→C→D$的路线,向点 D 运动,点 Q 只能在线段 AD 上运动.在点 P 从点 A 到点 D 的运动过程中,PQ 的中点 O 所经过的路径长为______.
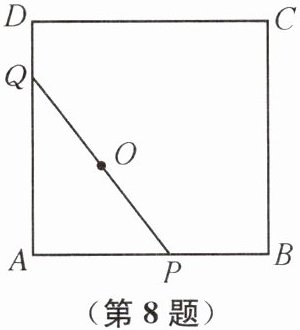

答案:
4π+8 提示:如图,①当点P在边AB上时,连接AO,则$AO=\frac{1}{2}PQ=4$,由圆的定义可知,点O的运动路径为$\overset{\frown}{EF}$;②当点P在边BC上时,可知PQ//AB,点O的运动路径为线段FG;③当点P在边CD上时,连接DO,则$DO=\frac{1}{2}PQ=4$,由圆的定义可知,点O的运动路径为$\overset{\frown}{GE}$.综上所述,PQ的中点O所经过的路径长为$\frac{90\pi×4}{180}+8+\frac{90\pi×4}{180}=4\pi+8$.

4π+8 提示:如图,①当点P在边AB上时,连接AO,则$AO=\frac{1}{2}PQ=4$,由圆的定义可知,点O的运动路径为$\overset{\frown}{EF}$;②当点P在边BC上时,可知PQ//AB,点O的运动路径为线段FG;③当点P在边CD上时,连接DO,则$DO=\frac{1}{2}PQ=4$,由圆的定义可知,点O的运动路径为$\overset{\frown}{GE}$.综上所述,PQ的中点O所经过的路径长为$\frac{90\pi×4}{180}+8+\frac{90\pi×4}{180}=4\pi+8$.

9. 如图,将边长为$\sqrt {2}cm$的正方形 ABCD 沿直线 l 向右翻动(不滑动).当正方形连续翻动8次后,正方形的中心 O 经过的路径长为
4π
cm.
答案:
4π 提示:连接OC.由四边形ABCD是正方形,边长为$\sqrt{2}$cm,易得OC=1 cm.当正方形向右翻动1次后,点O经过的路径长为$\frac{90\pi×1}{180}=\frac{\pi}{2}$(cm),所以当正方形向右翻动8次后,点O经过的路径长为$\frac{\pi}{2}×8=4\pi$(cm).
10. 如图,在矩形 ABCD 中,$AB= 1,BC= \sqrt {3}$,P 是边 AD 上的一个动点,连接 BP,点 C 关于直线 BP 的对称点为$C_{1}$,当点 P 运动时,点$C_{1}$也随之运动.若点 P 从点 A 运动到点 D,则线段$CC_{1}$扫过的区域的面积为______
$\pi+\frac{3\sqrt{3}}{4}$
.
答案:
$\pi+\frac{3\sqrt{3}}{4}$ 提示:当点P与点A重合时,设点C关于BP的对称点为C';当点P与点D重合时,设点C关于BP的对称点为C'',则BC₁=BC=BC'=BC''.所以当点P从点A运动到点D时,线段CC₁扫过的区域为扇形BC'C''和△BCC''.在△BCD中,因为∠BCD=90°,$BC=\sqrt{3}$,CD=AB=1,所以BD=2,所以∠DBC=30°,所以∠CBC''=60°,∠C'BC''=120°.又因为BC=BC'',所以△BCC''为等边三角形.过点C''作C''F⊥BC于点F,则$BF=\frac{\sqrt{3}}{2}$,所以$C''F=\frac{3}{2}$.所以线段CC₁扫过的区域的面积为$S_{扇形BC'C''}+S_{\triangle BCC''}=\frac{120\pi×(\sqrt{3})^{2}}{360}+\frac{1}{2}×\sqrt{3}×\frac{3}{2}=\pi+\frac{3\sqrt{3}}{4}$.
11. 如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ }$,D 是AB 上一点,以 CD 为直径的$\odot O$交 BC 于点 E,连接 AE 交$\odot O$于点 F,且$∠DFE= ∠BAC.$
(1) 求证:AB 与$\odot O$相切.
(2) 若$∠DFE= 30^{\circ },CD= 2$,求$\widehat {DE}$与弦 CD,CE 围成的阴影部分的面积.
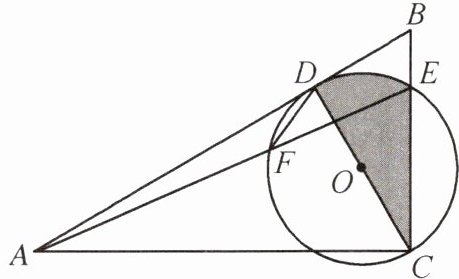
(1) 求证:AB 与$\odot O$相切.
(2) 若$∠DFE= 30^{\circ },CD= 2$,求$\widehat {DE}$与弦 CD,CE 围成的阴影部分的面积.

答案:
(1)证明:因为∠ACB=90°,所以∠BAC+∠B=90°.易知∠BCD=∠DFE,又因为∠DFE=∠BAC,所以∠BCD=∠BAC.所以∠BCD+∠B=90°,所以∠BDC=90°,所以AB⊥CD.又因为OD是$\odot O$的半径,所以AB与$\odot O$相切.
(2)解:连接OE,DE.因为CD为$\odot O$的直径,所以∠DEC=90°.因为∠DFE=30°,所以∠DOE=2∠DFE=60°,∠DCE=∠DFE=30°.所以$DE=\frac{1}{2}CD=1$,所以$CE=\sqrt{CD^{2}-DE^{2}}=\sqrt{3}$.因为OC=OD=1,所以$S_{\triangle COE}=\frac{1}{2}S_{\triangle CDE}=\frac{1}{2}×\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{4}$.所以$S_{阴影部分}=S_{扇形ODE}+S_{\triangle COE}=\frac{60\pi×1^{2}}{360}+\frac{\sqrt{3}}{4}=\frac{\pi}{6}+\frac{\sqrt{3}}{4}$.
(2)解:连接OE,DE.因为CD为$\odot O$的直径,所以∠DEC=90°.因为∠DFE=30°,所以∠DOE=2∠DFE=60°,∠DCE=∠DFE=30°.所以$DE=\frac{1}{2}CD=1$,所以$CE=\sqrt{CD^{2}-DE^{2}}=\sqrt{3}$.因为OC=OD=1,所以$S_{\triangle COE}=\frac{1}{2}S_{\triangle CDE}=\frac{1}{2}×\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{4}$.所以$S_{阴影部分}=S_{扇形ODE}+S_{\triangle COE}=\frac{60\pi×1^{2}}{360}+\frac{\sqrt{3}}{4}=\frac{\pi}{6}+\frac{\sqrt{3}}{4}$.
12. 如图,$\odot O$的半径为5,弦$AB= 6$,弦$AC⊥BD$,P 为 CD 的中点.若点 D 在圆上逆时针运动的路径长为$\frac {5π}{3}$,则点 P 运动的路径长为______.
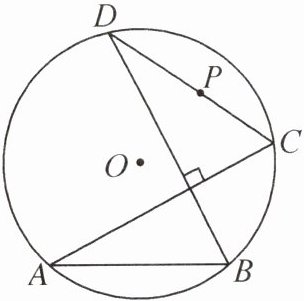

答案:
π 提示:如图,连接OA,OB,AD,OP,OD,OC,过点O作OH⊥AB于点H.因为AC⊥BD,所以∠DAC+∠ADB=90°.又因为∠DOC=2∠DAC,∠AOB=2∠ADB,所以∠DOC+∠AOB=180°.因为OH⊥AB,DP=PC,所以$AH=HB=\frac{1}{2}AB=3$,OP⊥CD,所以∠AOH=∠BOH,∠COP=∠DOP.所以∠AOH+∠COP=90°.又因为∠AOH+∠OAH=90°,所以∠COP=∠OAH.易证△OHA≌△CPO,所以OP=AH=3.易得DP=CP=OH=4.所以点P在以点O为圆心,3为半径的圆上运动.设点D在圆上逆时针运动的圆心角为n°,则由路径长为$\frac{5\pi}{3}$,得$\frac{n\pi×5}{180}=\frac{5\pi}{3}$,解得n=60.易知OD,OP的旋转角度相等,所以点P运动的路径长为$\frac{60\pi×3}{180}=\pi$.

π 提示:如图,连接OA,OB,AD,OP,OD,OC,过点O作OH⊥AB于点H.因为AC⊥BD,所以∠DAC+∠ADB=90°.又因为∠DOC=2∠DAC,∠AOB=2∠ADB,所以∠DOC+∠AOB=180°.因为OH⊥AB,DP=PC,所以$AH=HB=\frac{1}{2}AB=3$,OP⊥CD,所以∠AOH=∠BOH,∠COP=∠DOP.所以∠AOH+∠COP=90°.又因为∠AOH+∠OAH=90°,所以∠COP=∠OAH.易证△OHA≌△CPO,所以OP=AH=3.易得DP=CP=OH=4.所以点P在以点O为圆心,3为半径的圆上运动.设点D在圆上逆时针运动的圆心角为n°,则由路径长为$\frac{5\pi}{3}$,得$\frac{n\pi×5}{180}=\frac{5\pi}{3}$,解得n=60.易知OD,OP的旋转角度相等,所以点P运动的路径长为$\frac{60\pi×3}{180}=\pi$.

13. 如图,在边长为$2\sqrt {2}$的正方形 ABCD 中,P 是对角线 AC 上的一个动点(点 P 不与点 A,C 重合),连接 BP,将 BP 绕点 B 顺时针旋转$90^{\circ }$得到 BQ,连接 QP,与 BC 交于点 E,QP 的延长线与 AD(或 AD 的延长线)交于点 F,连接 CF,以 DF 为直径的圆交 CF 于点 M.
(1) 在点 P 从点 A 到点 C 的运动过程中,求点 M 运动的路径长.
(2) 求线段 AM 长的最小值.
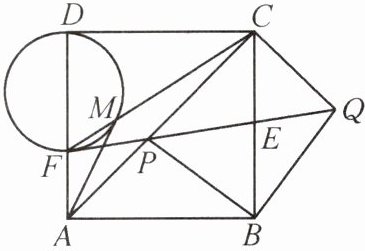
(1) 在点 P 从点 A 到点 C 的运动过程中,求点 M 运动的路径长.
(2) 求线段 AM 长的最小值.

答案:
(1)如图,连接DM,取CD的中点为J.因为DF是直径,所以∠DMF=90°,所以∠DMC=180° - ∠DMF=90°,所以点M在以CD为直径的$\odot J$上运动.当点P与点A重合时,M₁是$\overset{\frown}{CD}$(直径CD下方)的中点;当点P与点C重合时,M₂是$\overset{\frown}{CD}$(直径CD上方)的中点.所以点M的运动路径是图中的$\overset{\frown}{M₁M₂}$(实线),运动的路径长为$\sqrt{2}\pi$.

(2)如图,连接AJ,JM.易知$JM=\sqrt{2}$,$AJ=\sqrt{AD^{2}+JD^{2}}=\sqrt{10}$.因为AM≥AJ - JM,所以$AM\geq\sqrt{10}-\sqrt{2}$,即线段AM长的最小值为$\sqrt{10}-\sqrt{2}$.
(1)如图,连接DM,取CD的中点为J.因为DF是直径,所以∠DMF=90°,所以∠DMC=180° - ∠DMF=90°,所以点M在以CD为直径的$\odot J$上运动.当点P与点A重合时,M₁是$\overset{\frown}{CD}$(直径CD下方)的中点;当点P与点C重合时,M₂是$\overset{\frown}{CD}$(直径CD上方)的中点.所以点M的运动路径是图中的$\overset{\frown}{M₁M₂}$(实线),运动的路径长为$\sqrt{2}\pi$.

(2)如图,连接AJ,JM.易知$JM=\sqrt{2}$,$AJ=\sqrt{AD^{2}+JD^{2}}=\sqrt{10}$.因为AM≥AJ - JM,所以$AM\geq\sqrt{10}-\sqrt{2}$,即线段AM长的最小值为$\sqrt{10}-\sqrt{2}$.
查看更多完整答案,请扫码查看


