《2025年小题狂做九年级数学上册苏科版巅峰版》

1.(南通市模拟)给出下列方程：①$x^{2}+3x+1= 0$；②$\sqrt{4x+1}+1= 0$；③$x^{2}+2x+3= 0$；④$\frac{x}{x-1}= \frac{1}{x-1}$.其中有实数根的有(A)
A.1个
B.2个
C.3个
D.4个

答案： A

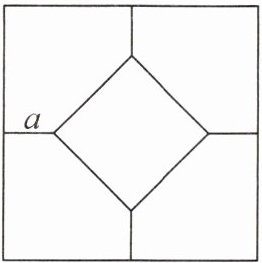
2. 如图,一块正方形地砖的图案是由4个全等的五边形和1个小正方形组成的,已知小正方形的面积和五边形的面积相等,并且图中线段a的长度为$\sqrt{10}-2$,则这块地砖的面积为( )


A.50
B.40
C.30
D.20

答案：
B 提示:如图,根据题意易知,点O为正方形ABCD,EFGH的中心,所以$S_{正方形EFGH}=4S_{\triangle EOF}$,$S_{正方形ABCD}=5S_{正方形EFGH}$.因为$S_{五边形AMFEP}=S_{正方形EFGH}$,所以$S_{五边形AMFEP}=4S_{\triangle EOF}$.因为$S_{五边形AMFEP}=\frac{1}{4}S_{正方形ABCD}-S_{\triangle EOF}$,所以$\frac{1}{4}S_{正方形ABCD}=5S_{\triangle EOF}$.设正方形ABCD的边长为$2x(x＞a)$,则$OF=OE=x-a$,所以$\frac{1}{4}\cdot 2x\cdot 2x=\frac{5}{2}(x-a)^2$,解得$x_1=\frac{(5-\sqrt{10})a}{3}$(舍去),$x_2=\frac{(5+\sqrt{10})a}{3}$.因为$a=\sqrt{10}-2$,所以$x=\sqrt{10}$.所以$S_{正方形ABCD}=2\sqrt{10}× 2\sqrt{10}=40$.

3.(泰州市靖江市模拟)若t是关于x的方程$ax^{2}+bx+c= 0(a≠0)$的根,则根的判别式$b^{2}-4ac的值和完全平方式M= (2at+b)^{2}$的值的大小关系是(A)
A.$b^{2}-4ac= M$
B.$b^{2}-4ac＞M$
C.$b^{2}-4ac＜M$
D.不能确定

答案： A

4. 已知a是方程$x^{2}-2024x+1= 0$的一个根,则$a^{2}-2023a+\frac{2024}{a^{2}+1}$的值为2023.

答案： 2023

5. 若α,β是方程$x^{2}-x-3= 0$的两个实数根,则$\frac{1}{α-1}+\frac{1}{β-1}= $$\frac{1}{3}$.

答案： $\frac{1}{3}$

6. 如果$ab≠1$,且$5a^{2}+2024a+9= 0$,$9b^{2}+2024b+5= 0$,那么$\frac{a}{b}$的值是$\frac{9}{5}$.

答案： $\frac{9}{5}$ 提示:由题意,得$b\neq 0$.在等式$9b^2+2024b+5=0$两边同时除以$b^2$,得$5\left(\frac{1}{b}\right)^2+2024× \frac{1}{b}+9=0$.因为$ab\neq 1$,所以$a\neq \frac{1}{b}$.又因为$5a^2+2024a+9=0$,所以$a,\frac{1}{b}$是方程$5x^2+2024x+9=0$的两个不相等的实数根.所以$\frac{a}{b}=a\cdot \frac{1}{b}=\frac{9}{5}$.

7. 新定义：将关于x的一元二次方程$m(x-a)^{2}+b= 0与n(x-a)^{2}+b= 0$称为“同类方程”,如$2(x-1)^{2}+3= 0与6(x-1)^{2}+3= 0$是“同类方程”.现有关于x的一元二次方程$2(x-1)^{2}+1= 0与(a+6)x^{2}-(b+8)x+6= 0$是“同类方程”,那么代数式$ax^{2}+bx+2024$的最大值为______.
2025

答案： 2025 提示:由题意,得$(a+6)x^2-(b+8)x+6=(a+6)(x-1)^2+1=(a+6)x^2-2(a+6)x+a+7$.所以$\begin{cases} b+8=2(a+6), \\ 6=a+7, \end{cases}$解得$\begin{cases} a=-1, \\ b=2. \end{cases}$所以$ax^2+bx+2024=-x^2+2x+2024=-(x-1)^2+2025$,所以当$x=1$时,原式取得最大值,为2025.

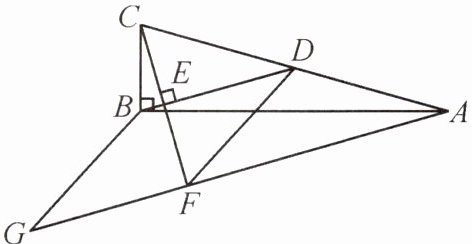
8. 如图,在$\triangle ABC$中,$\angle ABC= 90^{\circ}$,BD是边AC上的中线,过点C作$CE\perp BD$于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取$FG= BD$,连接BG,DF.若$AG= 13$,$CF= 6$,则四边形BDFG的周长为______20.

答案： 20 提示:易证四边形BDFG是平行四边形.因为$CF\perp BD$,$BD// AG$,所以$CF\perp AG$.又因为D是AC的中点,所以$BD=DF=\frac{1}{2}AC$.所以四边形BDFG是菱形.设$GF=x$,则$AF=13-x$,$AC=2x$.在$\text{Rt}\triangle ACF$中,由勾股定理,得$AF^2+CF^2=AC^2$,即$(13-x)^2+6^2=(2x)^2$,解得$x=5$(负值已舍).所以四边形BDFG的周长为$4GF=20$.

9. 在一次社团文化节上,中国象棋社开展了社员挑战活动,每名选手都只和其他选手比赛一局,每局赢者得2分,输者得0分,和棋双方各记1分.现有四位同学统计了比赛中全部选手的得分总数,总分分别是1054,1056,1060,1066.经核实,上述四位同学只有一位同学统计正确,则这次比赛中有______名选手参加比赛.
[答案]：33 提示:设这次比赛中有x名选手参加比赛.若$2× \frac{1}{2}x(x-1)=1054$,则解得x不为整数;若$2× \frac{1}{2}x(x-1)=1056$,则解得$x_1=33$,$x_2=-32$(舍去);若$2× \frac{1}{2}x(x-1)=1060$,则解得x不为整数;若$2× \frac{1}{2}x(x-1)=1066$,则解得x不为整数.因为只有一位同学统计正确,所以这次比赛中有33名选手参加比赛.

答案： 33 提示:设这次比赛中有x名选手参加比赛.若$2× \frac{1}{2}x(x-1)=1054$,则解得x不为整数;若$2× \frac{1}{2}x(x-1)=1056$,则解得$x_1=33$,$x_2=-32$(舍去);若$2× \frac{1}{2}x(x-1)=1060$,则解得x不为整数;若$2× \frac{1}{2}x(x-1)=1066$,则解得x不为整数.因为只有一位同学统计正确,所以这次比赛中有33名选手参加比赛.

10. 如果方程$x^{3}-7x^{2}+(10+k)x-2k= 0$的三个根可以作为一个等腰三角形的边长,则实数$k=$$\frac{25}{4}$或6.

答案： $\frac{25}{4}$或6 提示:方程可变形为$x^3-7x^2+10x+kx-2k=0$,即$x(x-5)(x-2)+k(x-2)=0$,所以$(x-2)(x^2-5x+k)=0$,所以$x-2=0$或$x^2-5x+k=0$,所以$x=2$是方程的一个根.因为方程的三个根可以作为一个等腰三角形的边长,所以$x^2-5x+k=0$有两个相等的根或$x^2-5x+k=0$有一个根是2.当$x^2-5x+k=0$有两个相等的根时,根的判别式$25-4k=0$,解得$k=\frac{25}{4}$,此时方程的根为$x=\frac{5}{2}$,所以三角形的三条边长分别为$2,\frac{5}{2},\frac{5}{2}$;当$x^2-5x+k=0$有一个根是2时,$k=6$,此时方程的根为$x=2$或$x=3$,所以三角形的三条边长分别为2,2,3.综上所述,k的值为$\frac{25}{4}$或6.

11. 已知关于x的一元二次方程$(a-6)x^{2}-8x+18= 0$有实数根.
(1)求a的最大整数值；
(2)当a取最大整数时,求$2x^{2}+\frac{32x}{x^{2}+8x-16}$的值.

答案： $(1)$求$a$的最大整数值
解：
因为方程$(a - 6)x^{2}-8x + 18 = 0$是一元二次方程且有实数根，所以$\begin{cases}a - 6\neq0\\\Delta =(-8)^{2}-4×(a - 6)×18\geq0\end{cases}$。
由$a - 6\neq0$得$a\neq6$。
由$\Delta = 64-72(a - 6)\geq0$，展开$64-72a + 432\geq0$，即$-72a\geq - 496$，解得$a\leq\frac{62}{9}\approx6.89$。
综上，$a$的取值范围是$a\leq\frac{62}{9}$且$a\neq6$，所以$a$的最大整数值为$a = 5$。
$(2)$当$a$取最大整数时，求$2x^{2}+\frac{32x}{x^{2}+8x - 16}$的值
解：
当$a = 5$时，方程为$(5 - 6)x^{2}-8x + 18 = 0$，即$-x^{2}-8x + 18 = 0$，移项得$x^{2}+8x=18$。
将$x^{2}+8x = 18$代入$2x^{2}+\frac{32x}{x^{2}+8x - 16}$中：
$2x^{2}+\frac{32x}{18 - 16}=2x^{2}+16x$，由$x^{2}+8x = 18$，两边同时乘以$2$得$2x^{2}+16x = 36$。
综上，$(1)$$\boldsymbol{a = 5}$；$(2)$$\boldsymbol{36}$。