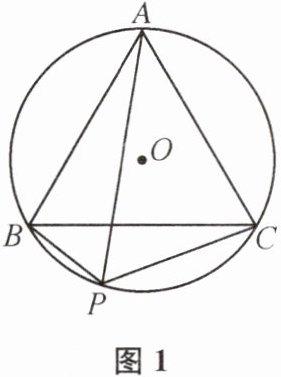
9. (1)如图1,已知△ABC是⊙O的内接正三角形,P为$\overset{\frown}{BC}$上一动点,求证:PA= PB+PC.
(2)如图2,四边形ABCD是⊙O的内接正方形,P为$\overset{\frown}{BC}$上一动点,求证:PA= PC+$\sqrt{2}$PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,P为$\overset{\frown}{BC}$上一动点,请探究PA,PB,PC三者之间的数量关系,并给出证明.
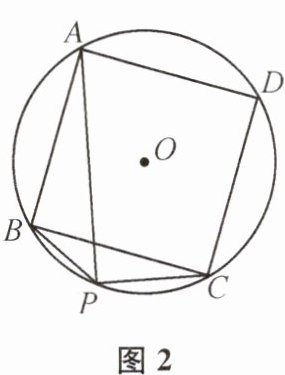

(2)如图2,四边形ABCD是⊙O的内接正方形,P为$\overset{\frown}{BC}$上一动点,求证:PA= PC+$\sqrt{2}$PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,P为$\overset{\frown}{BC}$上一动点,请探究PA,PB,PC三者之间的数量关系,并给出证明.



答案:
(1)证明:如图1,延长BP至点E,使PE=PC,连接CE.由条件,易得∠2=∠1=60°,∠3=∠4=60°,所以∠CPE=60°.所以△PCE是等边三角形,所以CE=PC,∠E=60°=∠3.又因为∠EBC=∠PAC,所以△BEC≌△APC.所以PA=EB=PB+PE=PB+PC.
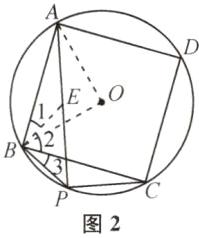
(2)证明:如图2,连接AO,BO,过点B作BE⊥PB交PA于点E.由条件,易得AB=BC,AB⊥BC,所以∠1+∠2=∠2+∠3=90°,所以∠1=∠3.又因为∠APB=$\frac{1}{2}$∠AOB=45°,所以∠BEP=45°,所以BP=BE.所以PE=$\sqrt{2}$PB,△ABE≌△CBP,所以PC=EA.所以PA=EA+PE=PC+$\sqrt{2}$PB.
(3)解:PA=$\sqrt{3}$PB+PC.证明如下:在AP上截取AQ=CP,连接BQ.易得∠BAQ=∠BCP,AB=CB.所以△ABQ≌△CBP,所以BQ=BP.又易得∠APB=30°,PQ=$\sqrt{3}$PB.所以PA=PQ+AQ=$\sqrt{3}$PB+PC.
(1)证明:如图1,延长BP至点E,使PE=PC,连接CE.由条件,易得∠2=∠1=60°,∠3=∠4=60°,所以∠CPE=60°.所以△PCE是等边三角形,所以CE=PC,∠E=60°=∠3.又因为∠EBC=∠PAC,所以△BEC≌△APC.所以PA=EB=PB+PE=PB+PC.
(2)证明:如图2,连接AO,BO,过点B作BE⊥PB交PA于点E.由条件,易得AB=BC,AB⊥BC,所以∠1+∠2=∠2+∠3=90°,所以∠1=∠3.又因为∠APB=$\frac{1}{2}$∠AOB=45°,所以∠BEP=45°,所以BP=BE.所以PE=$\sqrt{2}$PB,△ABE≌△CBP,所以PC=EA.所以PA=EA+PE=PC+$\sqrt{2}$PB.


(3)解:PA=$\sqrt{3}$PB+PC.证明如下:在AP上截取AQ=CP,连接BQ.易得∠BAQ=∠BCP,AB=CB.所以△ABQ≌△CBP,所以BQ=BP.又易得∠APB=30°,PQ=$\sqrt{3}$PB.所以PA=PQ+AQ=$\sqrt{3}$PB+PC.
10. 如图,正方形ABCD的边长为4,点E在边BC上运动,连接AE,过点B作BF⊥AE,垂足为F,以BF为边作正方形BFGH.当点E与点B重合时,点F,G,H与点B重合,则DH长的最大值是 ( )

A.8
B.$4\sqrt{5}$
C.$2\sqrt{5}+2$
D.$2\sqrt{5}+4$

A.8
B.$4\sqrt{5}$
C.$2\sqrt{5}+2$
D.$2\sqrt{5}+4$
答案:
C 提示:如图,取AB的中点M,连接MF,取BC的中点N,连接NH,ND.因为四边形ABCD,BFGH为正方形,BF⊥AE,所以BF=BH,MF=BM=$\frac{1}{2}$AB=$\frac{1}{2}$CB=BN=2.因为∠ABC=∠FBH=90°,所以∠MBF=∠NBH.所以△MBF≌△NBH(SAS),所以NH=MF=2.所以点H在以点N为圆心,2为半径的⊙N的一部分弧上运动.当点D,N,H依次共线时,DH最大,最大值为DN+NH.易得DN=$\sqrt{4^2 + 2^2}$=$2\sqrt{5}$.所以DH长的最大值为$2\sqrt{5}+2$.
C 提示:如图,取AB的中点M,连接MF,取BC的中点N,连接NH,ND.因为四边形ABCD,BFGH为正方形,BF⊥AE,所以BF=BH,MF=BM=$\frac{1}{2}$AB=$\frac{1}{2}$CB=BN=2.因为∠ABC=∠FBH=90°,所以∠MBF=∠NBH.所以△MBF≌△NBH(SAS),所以NH=MF=2.所以点H在以点N为圆心,2为半径的⊙N的一部分弧上运动.当点D,N,H依次共线时,DH最大,最大值为DN+NH.易得DN=$\sqrt{4^2 + 2^2}$=$2\sqrt{5}$.所以DH长的最大值为$2\sqrt{5}+2$.

11. 平面内一个正n边形,将平面内与正n边形的各顶点距离都小于等于边长的所有点组成的图形称为这个正n边形的"伴侣形".将正n边形内与其各顶点距离都大于等于边长的所有点组成的图形称为这个正n边形的"远伴侣形".(注:在半径为R的圆中,弧长l与所对的圆心角度数n之间的关系为$l= \frac{n}{360}× 2\pi R= \frac{n\pi R}{180}$)
【观察】如图1,边长为1的等边三角形ABC,分别以点A,B,C为圆心,AB长为半径画圆弧,则三条弧AB,BC,AC及其内部所组成的图形上的点到各顶点距离都小于等于1,我们把这个图形称为正三角形ABC的"伴侣形".
【判断】(1)______(填"是"或"不是")所有的正多边形都有"伴侣形",______(填"是"或"不是")所有的正多边形都有"远伴侣形".
【操作】(2)如图2,边长为1的正方形ABCD,请作出正方形ABCD的"伴侣形"(将此"伴侣形"打上阴影),求此正方形ABCD的"伴侣形"的周长.
【探究】(3)结合图3分析,若正n边形的边长为1,则当n= 7时,其"远伴侣形"的周长为______,则当n= 8时,其"远伴侣形"的周长为______.
【归纳】(4)边长为1的正n边形(n≥7),其"远伴侣形"的周长为______.

【观察】如图1,边长为1的等边三角形ABC,分别以点A,B,C为圆心,AB长为半径画圆弧,则三条弧AB,BC,AC及其内部所组成的图形上的点到各顶点距离都小于等于1,我们把这个图形称为正三角形ABC的"伴侣形".
【判断】(1)______(填"是"或"不是")所有的正多边形都有"伴侣形",______(填"是"或"不是")所有的正多边形都有"远伴侣形".
【操作】(2)如图2,边长为1的正方形ABCD,请作出正方形ABCD的"伴侣形"(将此"伴侣形"打上阴影),求此正方形ABCD的"伴侣形"的周长.
【探究】(3)结合图3分析,若正n边形的边长为1,则当n= 7时,其"远伴侣形"的周长为______,则当n= 8时,其"远伴侣形"的周长为______.
【归纳】(4)边长为1的正n边形(n≥7),其"远伴侣形"的周长为______.

答案:
(1)不是 不是
(2)解:正方形ABCD的“伴侣形”,如图1所示.设“伴侣形”的两个顶点为E,F,连接AE,DE和AF.由题意,得AD=AE=ED,则△AED为等边三角形,得∠DAE=60°,所以∠EAB=30°,同理∠FAD=30°,所以∠FAE=30°,则$C\overset{\frown}{EF}$=$\frac{30×\pi×1}{180}$=$\frac{\pi}{6}$,故正方形ABCD“伴侣形”的周长为$\frac{\pi}{6}×4$=$\frac{2\pi}{3}$.
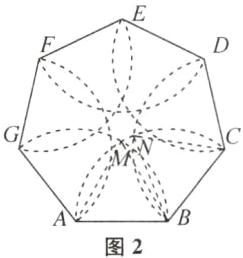
(3)$\frac{\pi}{3}$ $\frac{2\pi}{3}$ 提示:如图2,连接AM,BM,BN和NC.由题意,得AM=BM=AB=BC=BN=NC,则△ABM和△BCN都为等边三角形,得∠ABM=∠CBN=60°.因为∠ABC=$\frac{180°×(7 - 2)}{7}$=$\frac{900°}{7}$,所以∠MBN=∠ABC - ∠ABM - ∠CBN=$\frac{60°}{7}$,则$C\overset{\frown}{MN}$=$\frac{\frac{60}{7}×\pi×1}{180}$=$\frac{\pi}{21}$,故当n=7时,其“远伴侣形”的周长为$\frac{\pi}{21}×7$=$\frac{\pi}{3}$.同理,当n=8时,其“远伴侣形”的周长为$\frac{[\frac{180×(8 - 2)}{8}-120]×\pi×1}{180}×8$=$\frac{2\pi}{3}$.
(4)$\frac{(n - 6)\pi}{3}$ 提示:$\frac{[\frac{180×(n - 2)}{n}-120]×\pi×1}{180}×n=\frac{(n - 6)\pi}{3}$.
(1)不是 不是
(2)解:正方形ABCD的“伴侣形”,如图1所示.设“伴侣形”的两个顶点为E,F,连接AE,DE和AF.由题意,得AD=AE=ED,则△AED为等边三角形,得∠DAE=60°,所以∠EAB=30°,同理∠FAD=30°,所以∠FAE=30°,则$C\overset{\frown}{EF}$=$\frac{30×\pi×1}{180}$=$\frac{\pi}{6}$,故正方形ABCD“伴侣形”的周长为$\frac{\pi}{6}×4$=$\frac{2\pi}{3}$.


(3)$\frac{\pi}{3}$ $\frac{2\pi}{3}$ 提示:如图2,连接AM,BM,BN和NC.由题意,得AM=BM=AB=BC=BN=NC,则△ABM和△BCN都为等边三角形,得∠ABM=∠CBN=60°.因为∠ABC=$\frac{180°×(7 - 2)}{7}$=$\frac{900°}{7}$,所以∠MBN=∠ABC - ∠ABM - ∠CBN=$\frac{60°}{7}$,则$C\overset{\frown}{MN}$=$\frac{\frac{60}{7}×\pi×1}{180}$=$\frac{\pi}{21}$,故当n=7时,其“远伴侣形”的周长为$\frac{\pi}{21}×7$=$\frac{\pi}{3}$.同理,当n=8时,其“远伴侣形”的周长为$\frac{[\frac{180×(8 - 2)}{8}-120]×\pi×1}{180}×8$=$\frac{2\pi}{3}$.
(4)$\frac{(n - 6)\pi}{3}$ 提示:$\frac{[\frac{180×(n - 2)}{n}-120]×\pi×1}{180}×n=\frac{(n - 6)\pi}{3}$.
查看更多完整答案,请扫码查看


