11. 阅读以下材料:
为解方程$x^{4}-x^{2}-6= 0$,可设$x^{2}= y$,于是原方程可化为$y^{2}-y-6= 0$,解得$y_{1}= -2,y_{2}= 3$.当$y= -2$时,$x^{2}= -2$,无实数根;当$y= 3$时,$x^{2}= 3$,解得$x_{1}= \sqrt {3}$,$x_{2}= -\sqrt {3}$.所以原方程的实数根为$x_{1}= \sqrt {3},x_{2}= -\sqrt {3}$.
请参照材料中给出的解题方法,解下列方程:
(1)$(x^{2}-x)^{2}-4(x^{2}-x)-12= 0$;
(2)$\frac {2x-1}{x}-\frac {3x}{2x-1}= 2$;
(3)(2024徐州市新沂市期中)$x\sqrt {x}= x+\sqrt {x}$.
为解方程$x^{4}-x^{2}-6= 0$,可设$x^{2}= y$,于是原方程可化为$y^{2}-y-6= 0$,解得$y_{1}= -2,y_{2}= 3$.当$y= -2$时,$x^{2}= -2$,无实数根;当$y= 3$时,$x^{2}= 3$,解得$x_{1}= \sqrt {3}$,$x_{2}= -\sqrt {3}$.所以原方程的实数根为$x_{1}= \sqrt {3},x_{2}= -\sqrt {3}$.
请参照材料中给出的解题方法,解下列方程:
(1)$(x^{2}-x)^{2}-4(x^{2}-x)-12= 0$;
(2)$\frac {2x-1}{x}-\frac {3x}{2x-1}= 2$;
(3)(2024徐州市新沂市期中)$x\sqrt {x}= x+\sqrt {x}$.
答案:
解:
(1)设$y=x^{2}-x$,则原方程可化为$y^{2}-4y-12=0$,解得$y_{1}=-2$,$y_{2}=6$.当$y=-2$时,$x^{2}-x=-2$,即$x^{2}-x+2=0$,此时方程无实数根;当$y=6$时,$x^{2}-x=6$,即$x^{2}-x-6=0$,解得$x_{1}=-2$,$x_{2}=3$.所以原方程的实数根为$x_{1}=-2$,$x_{2}=3$.
(2)设$\frac{2x-1}{x}=y$,则原方程可化为$y-\frac{3}{y}=2$.去分母并整理,得$y^{2}-2y-3=0$,解得$y_{1}=-1$,$y_{2}=3$.当$y=-1$时,$\frac{2x-1}{x}=-1$,解之并检验得$x=\frac{1}{3}$;当$y=3$时,$\frac{2x-1}{x}=3$,解之并检验得$x=-1$.所以原方程的根为$x_{1}=\frac{1}{3}$,$x_{2}=-1$.
(3)设$\sqrt{x}=y$,其中$y\geqslant 0$,则$y^{2}=x$,所以原方程可转化为$y^{3}=y^{2}+y$,所以$y^{3}-y^{2}-y=0$,因式分解,得$y(y^{2}-y-1)=0$,所以$y=0$或$y^{2}-y-1=0$.当$y=0$时,$x=y^{2}=0$,由$y^{2}-y-1=0$,得$y_{1}=\frac{1+\sqrt{5}}{2}$,$y_{2}=\frac{1-\sqrt{5}}{2}$(不合题意,舍去).当$y=\frac{1+\sqrt{5}}{2}$时,$x=y^{2}=(\frac{1+\sqrt{5}}{2})^{2}=\frac{3+\sqrt{5}}{2}$.综上所述,该方程的解为$x_{1}=0$,$x_{2}=\frac{3+\sqrt{5}}{2}$.
(1)设$y=x^{2}-x$,则原方程可化为$y^{2}-4y-12=0$,解得$y_{1}=-2$,$y_{2}=6$.当$y=-2$时,$x^{2}-x=-2$,即$x^{2}-x+2=0$,此时方程无实数根;当$y=6$时,$x^{2}-x=6$,即$x^{2}-x-6=0$,解得$x_{1}=-2$,$x_{2}=3$.所以原方程的实数根为$x_{1}=-2$,$x_{2}=3$.
(2)设$\frac{2x-1}{x}=y$,则原方程可化为$y-\frac{3}{y}=2$.去分母并整理,得$y^{2}-2y-3=0$,解得$y_{1}=-1$,$y_{2}=3$.当$y=-1$时,$\frac{2x-1}{x}=-1$,解之并检验得$x=\frac{1}{3}$;当$y=3$时,$\frac{2x-1}{x}=3$,解之并检验得$x=-1$.所以原方程的根为$x_{1}=\frac{1}{3}$,$x_{2}=-1$.
(3)设$\sqrt{x}=y$,其中$y\geqslant 0$,则$y^{2}=x$,所以原方程可转化为$y^{3}=y^{2}+y$,所以$y^{3}-y^{2}-y=0$,因式分解,得$y(y^{2}-y-1)=0$,所以$y=0$或$y^{2}-y-1=0$.当$y=0$时,$x=y^{2}=0$,由$y^{2}-y-1=0$,得$y_{1}=\frac{1+\sqrt{5}}{2}$,$y_{2}=\frac{1-\sqrt{5}}{2}$(不合题意,舍去).当$y=\frac{1+\sqrt{5}}{2}$时,$x=y^{2}=(\frac{1+\sqrt{5}}{2})^{2}=\frac{3+\sqrt{5}}{2}$.综上所述,该方程的解为$x_{1}=0$,$x_{2}=\frac{3+\sqrt{5}}{2}$.
12. 已知方程$x^{2}-2|x|-15= 0$,则此方程的所有实数根的和为 (
A.0
B.-2
C.2
D.8
A
)A.0
B.-2
C.2
D.8
答案:
A 提示:①当$x\geqslant 0$时,方程可化为$x^{2}-2x-15=0$,即$(x+3)(x-5)=0$,解得$x_{1}=-3$(舍去),$x_{2}=5$;②当$x<0$时,方程可化为$x^{2}+2x-15=0$,即$(x-3)(x+5)=0$,解得$x_{3}=3$(舍去),$x_{4}=-5$.所以此方程的所有实数根的和为$5+(-5)=0$.
13. 已知实数$a,b满足(a^{2}+4a+6)(2b^{2}-4b+7)\leqslant 10$,求$a+2b= $
0
.
答案:
0 提示:因为$(a^{2}+4a+6)(2b^{2}-4b+7)\leqslant 10$,所以$(a^{2}+4a+4+2)(2b^{2}-4b+2+5)\leqslant 10$,所以$[(a+2)^{2}+2][2(b-1)^{2}+5]\leqslant 10$.因为$(a+2)^{2}\geqslant 0$,$(b-1)^{2}\geqslant 0$,所以$(a+2)^{2}+2\geqslant 2$,$2(b-1)^{2}+5\geqslant 5$.所以$[(a+2)^{2}+2][2(b-1)^{2}+5]=10$,所以$a+2=0$,$b-1=0$,所以$a=-2$,$b=1$,所以$a+2b=-2+2=0$.
14. “转化”是一种重要的数学思想.用“转化”的数学思想,我们可以解一些新的方程,例如:
解无理方程:$\sqrt {x+1}= 2$.
解:方程两边同时平方,得$x+1= 4$,解这个一元一次方程,得$x= 3$.
检验:当$x= 3$时,左边$=\sqrt {3+1}= 2= $右边,所以,$x= 3$是原方程的解.
通过“方程两边平方”,有可能产生增根,必须对解得的根进行检验.
通过上面的学习,请解决以下两个问题:
(1) 解无理方程:$\sqrt {2x+3}= x$;
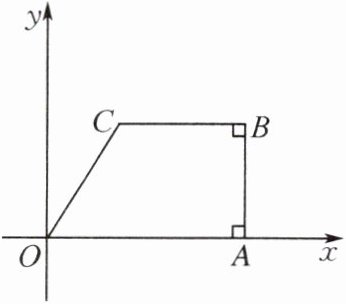
(2) 如图,在平面直角坐标系$xOy$中,点$B(5,3),∠OAB= ∠B= 90^{\circ },OC+BC= 7$,求点$C$的坐标.
]
解无理方程:$\sqrt {x+1}= 2$.
解:方程两边同时平方,得$x+1= 4$,解这个一元一次方程,得$x= 3$.
检验:当$x= 3$时,左边$=\sqrt {3+1}= 2= $右边,所以,$x= 3$是原方程的解.
通过“方程两边平方”,有可能产生增根,必须对解得的根进行检验.
通过上面的学习,请解决以下两个问题:
(1) 解无理方程:$\sqrt {2x+3}= x$;
(2) 如图,在平面直角坐标系$xOy$中,点$B(5,3),∠OAB= ∠B= 90^{\circ },OC+BC= 7$,求点$C$的坐标.
]

答案:
解:
(1)方程两边同时平方,得$2x+3=x^{2}$,解得$x=3$或$x=-1$.检验:当$x=3$时,左边$=\sqrt{2× 3+3}=3=$右边;当$x=-1$时,左边$=\sqrt{2× (-1)+3}=1\neq$右边.所以原方程的解为$x=3$.
(2)设点$C(x,3)$,则$OC=\sqrt{x^{2}+9}$,$BC=5-x$.因为$OC+BC=7$,所以$\sqrt{x^{2}+9}+(5-x)=7$,所以$\sqrt{x^{2}+9}=x+2$,两边同时平方,得$x^{2}+9=x^{2}+4x+4$,解得$x=\frac{5}{4}$.经检验,$x=\frac{5}{4}$是原方程的解.所以点$C(\frac{5}{4},3)$.
(1)方程两边同时平方,得$2x+3=x^{2}$,解得$x=3$或$x=-1$.检验:当$x=3$时,左边$=\sqrt{2× 3+3}=3=$右边;当$x=-1$时,左边$=\sqrt{2× (-1)+3}=1\neq$右边.所以原方程的解为$x=3$.
(2)设点$C(x,3)$,则$OC=\sqrt{x^{2}+9}$,$BC=5-x$.因为$OC+BC=7$,所以$\sqrt{x^{2}+9}+(5-x)=7$,所以$\sqrt{x^{2}+9}=x+2$,两边同时平方,得$x^{2}+9=x^{2}+4x+4$,解得$x=\frac{5}{4}$.经检验,$x=\frac{5}{4}$是原方程的解.所以点$C(\frac{5}{4},3)$.
查看更多完整答案,请扫码查看


