搜索
9. 在平面直角坐标系xOy中,以原点O为圆心的圆过点$A(13,0)$,直线$y= kx-3k+4与\odot O$交于B,C两点,则弦BC长的最小值为______.
答案：
24 提示:因为直线y=kx - 3k+4必过点D(3,4),所以最短的弦BC是过点D且与⊙O中经过点D的直径垂直的弦,如图所示.由题意,得⊙O的半径为13,所以OB=13.又因为OD=√(3²+4²)=5,OD⊥BC,所以BD=√(OB² - OD²)=12.所以BC=2BD=24,所以弦BC长的最小值为24.
24 提示:因为直线y=kx - 3k+4必过点D(3,4),所以最短的弦BC是过点D且与⊙O中经过点D的直径垂直的弦,如图所示.由题意,得⊙O的半径为13,所以OB=13.又因为OD=√(3²+4²)=5,OD⊥BC,所以BD=√(OB² - OD²)=12.所以BC=2BD=24,所以弦BC长的最小值为24.
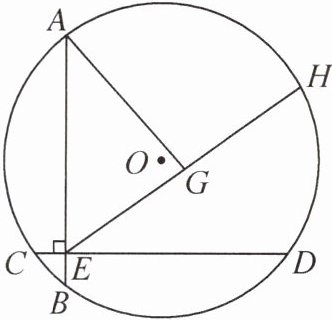
10. 如图,AB,CD是$\odot O$中的两条弦,相交于点E,且$AB⊥CD$,$AE= DE$,H为$\overset{\frown}{AD}$上一动点,G为HE的中点.若$CE= 1$,$DE= 7$,连接AG,则AG长的最小值为______.
答案：
(√130 - 5)/2 提示:如图1,连接AO,DO,EO,过点O分别作OK⊥AE,交AE于点K,OF⊥CD,交DE于点F.由题意,可得AE=DE=7,CD=CE+DE=8.因为OF⊥CD,所以CF=DF=1/2CD=4,所以EF=CF - CE=3.因为AE=DE,OA=OD,OE=OE,所以△AOE≌△DOE(SSS),所以∠AEO=∠DEO=1/2∠AED.因为OK⊥AE,OF⊥CD,所以OK=OF.因为AB⊥CD,所以∠AED=90°,所以四边形OKEF是正方形,所以OF=EF=3,所以OA=OD=√(OF²+DF²)=5,OE=√(OF²+EF²)=3√2.
如图2,取OE的中点M,连接MG,OH.因为M是OE的中点,G为HE的中点,所以MG=1/2OH=5/2,所以点G在以点M为圆心,5/2为半径的圆上运动.连接AM交⊙M于点G',过点M作MN⊥AE于点N.所以当A,G,M三点依次共线时,即点G和点G'重合时,AG的值最小.因为M是OE的中点,所以EM=1/2OE=3√2/2.因为MN⊥AE,∠NEM=1/2∠AED=45°,所以∠NME=45°,所以△NME是等腰直角三角形.所以MN=EN=√2/2ME=3/2,所以AN=AE - NE=11/2,所以AM=√(AN²+MN²)=√130/2,AG'=AM - G'M=√130/2 - 5/2.所以AG长的最小值为(√130 - 5)/2.
(√130 - 5)/2 提示:如图1,连接AO,DO,EO,过点O分别作OK⊥AE,交AE于点K,OF⊥CD,交DE于点F.由题意,可得AE=DE=7,CD=CE+DE=8.因为OF⊥CD,所以CF=DF=1/2CD=4,所以EF=CF - CE=3.因为AE=DE,OA=OD,OE=OE,所以△AOE≌△DOE(SSS),所以∠AEO=∠DEO=1/2∠AED.因为OK⊥AE,OF⊥CD,所以OK=OF.因为AB⊥CD,所以∠AED=90°,所以四边形OKEF是正方形,所以OF=EF=3,所以OA=OD=√(OF²+DF²)=5,OE=√(OF²+EF²)=3√2.
如图2,取OE的中点M,连接MG,OH.因为M是OE的中点,G为HE的中点,所以MG=1/2OH=5/2,所以点G在以点M为圆心,5/2为半径的圆上运动.连接AM交⊙M于点G',过点M作MN⊥AE于点N.所以当A,G,M三点依次共线时,即点G和点G'重合时,AG的值最小.因为M是OE的中点,所以EM=1/2OE=3√2/2.因为MN⊥AE,∠NEM=1/2∠AED=45°,所以∠NME=45°,所以△NME是等腰直角三角形.所以MN=EN=√2/2ME=3/2,所以AN=AE - NE=11/2,所以AM=√(AN²+MN²)=√130/2,AG'=AM - G'M=√130/2 - 5/2.所以AG长的最小值为(√130 - 5)/2. 11.【问题提出】
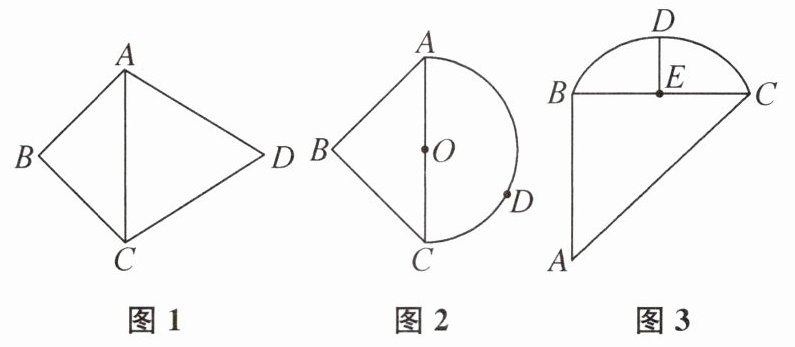
(1)如图1,在等腰直角三角形ABC中,$∠B= 90^{\circ }$,$\triangle ACD$为等边三角形,$AD= 6$,则线段BD的长为______.
【问题解决】
(2)如图2,在等腰直角三角形ABC中,$∠B= 90^{\circ }$,$AC= 4\sqrt {2}$,以AC为直径作半圆O,D为$\overset{\frown}{AC}$上一动点,求点B,D之间的最大距离.
【问题探究】
(3)一次手工制作课程中,老师要求小明和小丽制作一种特殊的部件,部件的要求如图3,它由直角三角形ABC以及弓形BDC组成,其中$∠B= 90^{\circ }$,$AB= 7$,$BC= 8$,$DE= 2$,E为BC的中点,$DE⊥BC$.小明和小丽在讨论这个部件,小丽说点A到$\overset{\frown}{BC}$的最大距离是点A,D之间的距离,小明说不对,你认为谁的说法正确?请说明理由,并求出点A到$\overset{\frown}{BC}$的最大距离.
(1)如图1,在等腰直角三角形ABC中,$∠B= 90^{\circ }$,$\triangle ACD$为等边三角形,$AD= 6$,则线段BD的长为______.
【问题解决】
(2)如图2,在等腰直角三角形ABC中,$∠B= 90^{\circ }$,$AC= 4\sqrt {2}$,以AC为直径作半圆O,D为$\overset{\frown}{AC}$上一动点,求点B,D之间的最大距离.
【问题探究】
(3)一次手工制作课程中,老师要求小明和小丽制作一种特殊的部件,部件的要求如图3,它由直角三角形ABC以及弓形BDC组成,其中$∠B= 90^{\circ }$,$AB= 7$,$BC= 8$,$DE= 2$,E为BC的中点,$DE⊥BC$.小明和小丽在讨论这个部件,小丽说点A到$\overset{\frown}{BC}$的最大距离是点A,D之间的距离,小明说不对,你认为谁的说法正确?请说明理由,并求出点A到$\overset{\frown}{BC}$的最大距离.
答案：
解:
(1)3+3√3
(2)如图1,连接BO并延长交⌢AC于点D'.当点D与点D'重合时,点B,D之间的距离最大.理由如下:
在⌢AC上取异于点D'的点D,连接BD,OD.在△BOD中,BO+OD＞BD.因为OD'=OD,所以BO+OD'＞BD,即BD'＞BD.在等腰直角三角形ABC中,因为O为AC的中点,所以BO=AO=$\frac{1}{2}$AC=2√2,所以BD'=BO+OD'=4√2,所以点B,D之间的最大距离为4√2.
(3)小明的说法正确.理由如下:
如图2,过点A作AF⊥DE,交DE的延长线于点F.因为E为BC的中点,DE⊥BC,所以⌢BC所在圆的圆心O在直线DF上.设⊙O的半径为r,连接BO,AD,连接AO并延长交⌢BC于点D'.在△AOD中,AO+OD＞AD,且OD'=OD,所以AO+OD'=AD'＞AD.同理可知,当点D移动到⌢BC任意位置且不与点D'重合时,AD'＞AD,所以点A到⌢BC的最大距离为AD'的长,所以小明的说法正确.在Rt△BOE中,BO=r,EO=DO - DE=r - 2,BE=$\frac{1}{2}$BC=4且BO²=BE²+EO²,所以r²=4²+(r - 2)²,解得r=5,所以EO=3.因为∠F=∠ABC=∠BEF=90°,所以四边形AFEB是矩形,EF=AB=7,AF=BE=4.所以OF=EF - EO=4.在Rt△AOF中,AO=√(AF²+OF²)=4√2.所以AD'=AO+OD'=4√2+5,所以点A到⌢BC的最大距离为4√2+5.
解:
(1)3+3√3
(2)如图1,连接BO并延长交⌢AC于点D'.当点D与点D'重合时,点B,D之间的距离最大.理由如下:
在⌢AC上取异于点D'的点D,连接BD,OD.在△BOD中,BO+OD＞BD.因为OD'=OD,所以BO+OD'＞BD,即BD'＞BD.在等腰直角三角形ABC中,因为O为AC的中点,所以BO=AO=$\frac{1}{2}$AC=2√2,所以BD'=BO+OD'=4√2,所以点B,D之间的最大距离为4√2.
(3)小明的说法正确.理由如下:
如图2,过点A作AF⊥DE,交DE的延长线于点F.因为E为BC的中点,DE⊥BC,所以⌢BC所在圆的圆心O在直线DF上.设⊙O的半径为r,连接BO,AD,连接AO并延长交⌢BC于点D'.在△AOD中,AO+OD＞AD,且OD'=OD,所以AO+OD'=AD'＞AD.同理可知,当点D移动到⌢BC任意位置且不与点D'重合时,AD'＞AD,所以点A到⌢BC的最大距离为AD'的长,所以小明的说法正确.在Rt△BOE中,BO=r,EO=DO - DE=r - 2,BE=$\frac{1}{2}$BC=4且BO²=BE²+EO²,所以r²=4²+(r - 2)²,解得r=5,所以EO=3.因为∠F=∠ABC=∠BEF=90°,所以四边形AFEB是矩形,EF=AB=7,AF=BE=4.所以OF=EF - EO=4.在Rt△AOF中,AO=√(AF²+OF²)=4√2.所以AD'=AO+OD'=4√2+5,所以点A到⌢BC的最大距离为4√2+5.
查看更多完整答案，请扫码查看
