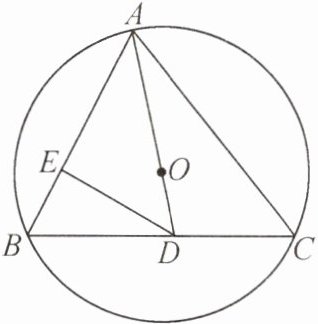
10. 如图,已知锐角三角形 ABC 内接于$\odot O$,连接 AO 并延长,交 BC 于点 D.
(1)求证:$∠ACB+∠BAD= 90^{\circ }.$
(2)过点 D 作$DE⊥AB$于点 E,若$∠ADC= 2∠ACB$,求证:$AC= 2DE.$
]
(1)求证:$∠ACB+∠BAD= 90^{\circ }.$
(2)过点 D 作$DE⊥AB$于点 E,若$∠ADC= 2∠ACB$,求证:$AC= 2DE.$
]

答案:
(1)证明:延长AD交$\odot O$于点F,连接BF.因为AF为$\odot O$的直径,所以∠ABF=90°,所以∠AFB+∠BAD=90°.因为∠AFB=∠ACB,所以∠ACB+∠BAD=90°.
(2)证明:过点O作OH⊥AC于点H,连接BO,CO.易知∠AOB=2∠ACB.又因为∠ADC=2∠ACB,所以∠AOB=∠ADC,所以180°−∠AOB=180°−∠ADC,即∠BOD=∠BDO,所以BD=BO.所以BD=OA.因为OH⊥AC,OA=OC,所以$AH=CH=\frac{1}{2}AC$,$∠AOH=\frac{1}{2}∠AOC$.又因为$∠ABD=\frac{1}{2}∠AOC$,所以∠ABD=∠AOH.又因为OH⊥AC,DE⊥AB,所以∠OHA=∠BED=90°.所以△BED≌△OHA,所以DE=AH,所以AC=2AH=2DE.
(1)证明:延长AD交$\odot O$于点F,连接BF.因为AF为$\odot O$的直径,所以∠ABF=90°,所以∠AFB+∠BAD=90°.因为∠AFB=∠ACB,所以∠ACB+∠BAD=90°.
(2)证明:过点O作OH⊥AC于点H,连接BO,CO.易知∠AOB=2∠ACB.又因为∠ADC=2∠ACB,所以∠AOB=∠ADC,所以180°−∠AOB=180°−∠ADC,即∠BOD=∠BDO,所以BD=BO.所以BD=OA.因为OH⊥AC,OA=OC,所以$AH=CH=\frac{1}{2}AC$,$∠AOH=\frac{1}{2}∠AOC$.又因为$∠ABD=\frac{1}{2}∠AOC$,所以∠ABD=∠AOH.又因为OH⊥AC,DE⊥AB,所以∠OHA=∠BED=90°.所以△BED≌△OHA,所以DE=AH,所以AC=2AH=2DE.
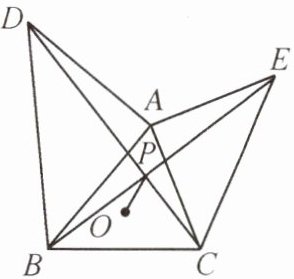
11. 如图,$BC= 6$,A 为平面内一动点,且$∠BAC= 60^{\circ }$,点 O 为$\triangle ABC$的外心,分别以 AB,AC为腰向$\triangle ABC$外作等腰直角三角形 ABD 与等腰直角三角形 ACE,连接 BE,CD 交于点 P,则 OP 长的最小值是___.
]
]

答案:
$3−\sqrt{3}$ 提示:因为△ABD与△ACE均是等腰直角三角形,所以易证△DAC≌△BAE,所以∠ADC=∠ABE.记AB与CD的交点为M,则∠AMD=∠BMP.因为∠BAD=90°,所以∠ADC+∠AMD=90°.所以∠ABE+∠BMP=90°,所以∠BPC=90°,所以点P在以BC为直径的圆上.连接OB,OC.因为点O为△ABC的外心,∠BAC=60°,所以∠BOC=120°,所以∠OBC=30°.如图,当PO⊥BC时,OP的值最小.延长PO交BC于点H,则PH⊥BC.因为BC=6,所以BH=CH=PH=3.因为$OH=\frac{\sqrt{3}}{3}BH=\sqrt {3}$,所以OP=PH−OH=3−$\sqrt{3}$.

$3−\sqrt{3}$ 提示:因为△ABD与△ACE均是等腰直角三角形,所以易证△DAC≌△BAE,所以∠ADC=∠ABE.记AB与CD的交点为M,则∠AMD=∠BMP.因为∠BAD=90°,所以∠ADC+∠AMD=90°.所以∠ABE+∠BMP=90°,所以∠BPC=90°,所以点P在以BC为直径的圆上.连接OB,OC.因为点O为△ABC的外心,∠BAC=60°,所以∠BOC=120°,所以∠OBC=30°.如图,当PO⊥BC时,OP的值最小.延长PO交BC于点H,则PH⊥BC.因为BC=6,所以BH=CH=PH=3.因为$OH=\frac{\sqrt{3}}{3}BH=\sqrt {3}$,所以OP=PH−OH=3−$\sqrt{3}$.

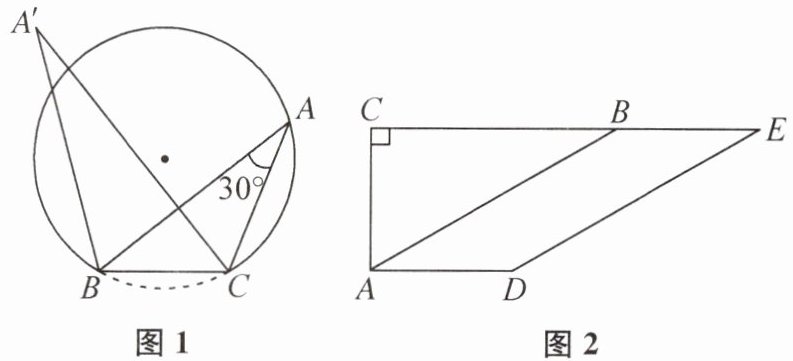
12. 【探究情境】已知线段$BC= 4$,使用作图工具作$∠BAC= 30^{\circ }$,尝试操作后,学习小组发现:点 A 的位置不唯一,它在以 BC 为弦的圆弧上(点 B,C 除外)……小华同学画出了符合要求的一条圆弧(图1),即圆中的$\widehat {BAC}.$
【展示交流】
(1)在展示交流中经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形外部,我们记为点$A'$,请你利用图1证明$∠BA'C<30^{\circ }.$
【提出问题】
(2)展示交流后,小华同学提出了下列新问题,请你帮助解决.
①该弧所在圆的半径长为___;
②$\triangle ABC$面积的最大值为___.
【拓展应用】
(3)如图 2,在$Rt\triangle ABC$中,$∠BCA= 90^{\circ },∠CBA= 30^{\circ },AC= 4$. 将 AB 沿CB 方向平移 m 个单位长度至 DE,点A,B 的对应点分别为 D,E. 是否存在这样的 m,使得线段 DE 上有一点 P 满足$∠CPA= 45^{\circ }$,且此时四边形 ADEB 的面积最大?若存在,求出此时的平移距离 m;若不存在,说明理由.
]
【展示交流】
(1)在展示交流中经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形外部,我们记为点$A'$,请你利用图1证明$∠BA'C<30^{\circ }.$
【提出问题】
(2)展示交流后,小华同学提出了下列新问题,请你帮助解决.
①该弧所在圆的半径长为___;
②$\triangle ABC$面积的最大值为___.
【拓展应用】
(3)如图 2,在$Rt\triangle ABC$中,$∠BCA= 90^{\circ },∠CBA= 30^{\circ },AC= 4$. 将 AB 沿CB 方向平移 m 个单位长度至 DE,点A,B 的对应点分别为 D,E. 是否存在这样的 m,使得线段 DE 上有一点 P 满足$∠CPA= 45^{\circ }$,且此时四边形 ADEB 的面积最大?若存在,求出此时的平移距离 m;若不存在,说明理由.
]

答案:
(1)证明:设A'B交$\odot O$于点E,连接CE.由圆周角定理可知,∠BEC=∠BAC=30°.因为∠BEC是△A'EC的外角,所以∠BEC>∠BA'C,所以∠BA'C<30°.
(2)①4 提示:设点O为圆心,连接BO,CO.因为∠BAC=30°,所以∠BOC=60°.因为OB=OC,所以△OBC是等边三角形,所以OB=OC=BC=4,即半径为4.
②$8+4\sqrt {3}$ 提示:△ABC以BC为底边,BC=4,当点A到边BC的距离最大时,△ABC的面积最大.如图1,过点O作OE⊥BC于点E,延长EO,交$\odot O$于点D,以BC为底,则当点A与点D重合时,△ABC的面积最大.所以BE=CE=2,DO=BO=4,所以$OE=\sqrt {BO^{2}-BE^{2}}=2\sqrt {3}$,所以$DE=DO+OE=4+2\sqrt {3}$.所以△ABC的最大面积为$\frac{1}{2}×4×(4+2\sqrt {3})=8+4\sqrt {3}$.
(3)解:存在.如图2,以AC为斜边作等腰直角三角形AOC,以点O为圆心,OC为半径作$\odot O$,交边BC于点F,交射线AD于点D'.由【探究情境】可知,当点P在以AC为弦的$\widehat {AFC}$(不含点A,C)上时,∠CPA=45°.又因为P是线段DE上一点,所以当点P运动到点D'时,AD的长最大,此时四边形ADEB的面积也最大.由题易证△ACD'为等腰直角三角形,所以AD'=AC=4,即m=4.


(1)证明:设A'B交$\odot O$于点E,连接CE.由圆周角定理可知,∠BEC=∠BAC=30°.因为∠BEC是△A'EC的外角,所以∠BEC>∠BA'C,所以∠BA'C<30°.
(2)①4 提示:设点O为圆心,连接BO,CO.因为∠BAC=30°,所以∠BOC=60°.因为OB=OC,所以△OBC是等边三角形,所以OB=OC=BC=4,即半径为4.
②$8+4\sqrt {3}$ 提示:△ABC以BC为底边,BC=4,当点A到边BC的距离最大时,△ABC的面积最大.如图1,过点O作OE⊥BC于点E,延长EO,交$\odot O$于点D,以BC为底,则当点A与点D重合时,△ABC的面积最大.所以BE=CE=2,DO=BO=4,所以$OE=\sqrt {BO^{2}-BE^{2}}=2\sqrt {3}$,所以$DE=DO+OE=4+2\sqrt {3}$.所以△ABC的最大面积为$\frac{1}{2}×4×(4+2\sqrt {3})=8+4\sqrt {3}$.
(3)解:存在.如图2,以AC为斜边作等腰直角三角形AOC,以点O为圆心,OC为半径作$\odot O$,交边BC于点F,交射线AD于点D'.由【探究情境】可知,当点P在以AC为弦的$\widehat {AFC}$(不含点A,C)上时,∠CPA=45°.又因为P是线段DE上一点,所以当点P运动到点D'时,AD的长最大,此时四边形ADEB的面积也最大.由题易证△ACD'为等腰直角三角形,所以AD'=AC=4,即m=4.


查看更多完整答案,请扫码查看


