《2025年小题狂做九年级数学上册苏科版巅峰版》

1. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下点P的坐标不满足要求的是 (C)
A.(3,5)
B.(-3,5)
C.(-1,7)
D.(1,-3)

答案： C 提示:设直线MN的表达式为y=kx+b，所以{k+b=2,3k+b=-3}，解得{k=-5/2,b=9/2}，所以y=-5/2x+9/2。当x=3时，y=-5/2×3+9/2=-3≠5，故点(3,5)不在直线MN上，根据不在同一直线上的三点确定一个圆，得点(3,5)与点M(1,2)，N(3,-3)可以确定一个圆，故选项A不符合题意；当x=-3时，y=-5/2×(-3)+9/2=12≠5，同理可知，选项B不符合题意；当x=-1时，y=-5/2×(-1)+9/2=7，故(-1,7)在直线MN上，故不能确定一个圆，故选项C符合题意；当x=1时，y=-5/2×1+9/2=2≠-3，同理可知，选项D不符合题意。

2. 平面内有不在同一条直线上的4个点,过其中3个点作圆,可以作出n个圆,那么n的值不可能为 (B)
A.1
B.2
C.3
D.4

答案： B

3. 已知平面直角坐标系xOy中的三点A(3,0),B(5,0),C(0,4),⊙P经过A,B,C三点,则点P的坐标为 (C)
A.(6,8)
B.(4,5)
C.$(4,\frac{31}{8})$
D.$(4,\frac{33}{8})$

答案： C

4. 如图是由三个大小相同的正方形组成的“品”字形轴对称图案,测得顶点A,B之间的距离为5.现用一个等边三角形纸片将其完全覆盖,当此等边三角形面积最小时,它的外接圆半径是 ( )


A.$\frac{5+2\sqrt{3}}{3}$
B.$\frac{8+2\sqrt{3}}{3}$
C.$\frac{5+4\sqrt{3}}{3}$
D.$\frac{8+4\sqrt{3}}{3}$

答案：
B 提示:如图，面积最小的等边三角形为△EFG，⊙O为△EFG的外接圆，设⊙O的半径为r，小正方形的边长为x。根据图形的对称性可知，EN⊥FG，AM⊥FG，HN=AM=2x，NM=AH=1/2x，BN=x，所以BM=BN+NM=3/2x。因为在Rt△ABM中，AB²=AM²+BM²，所以5²=(2x)²+(3/2x)²，解得x=2(负值已舍)，所以HN=4，AH=1。因为∠FEG=60°，EN⊥FG，所以∠FEN=30°，所以AE=2AH=2。所以EH=√(AE² - AH²)=√3，所以EN=EH+HN=4+√3。连接OG。易知OG=OE=r=2ON，所以EN=OE+ON=3/2r。所以外接圆半径是r=2/3EN=(8 + 2√3)/3。

5. 如图,在$□ ABCD$中,$AB= 3,BC= 6,\angle ABC= 60^\circ$.点P沿着折线段B-C-D-B运动.若点P在运动的过程中,$\triangle PAB$的外心O在$□ ABCD$的边上,则符合条件的点P有______个.

答案：
4 提示:如图，作线段AB的垂直平分线MN，分别交AB，BC于点F，E。因为AB=3，所以BF=1/2AB=3/2。因为∠ABC=60°，所以∠BEF=90° - 60°=30°，所以BE=2BF=3，所以CE=BC - BE=6 - 3=3。因为△PAB的外心一定在直线MN上，所以当△PAB的外心O在▱ABCD的边上时，△PAB的外心只可能落在直线MN与AB，BC的交点F，E处，所以点P在以点F为圆心，BF为半径的圆上，或以点E为圆心，BE为半径的圆上。如图，⊙E，⊙F与BC，CD，BD的交点即为点P的位置。因为BE=CE，所以点C在⊙E上，所以符合条件的点P有4个。

6. 若等腰三角形ABC内接于半径为5cm的$\odot O$,且底边$BC= 8cm$,则$\triangle ABC$的面积是8cm²或32cm².

答案： 8cm²或32cm²

7. 如图,已知等边三角形ABC内接于$\odot O$,P为$\overset{\frown}{AB}$上任意一点(点P不与点A,B重合),连接PB,PO,取BC的中点D,OP的中点E,连接DE.若$\angle OED= \alpha$,则$\angle PBC$的度数为______60° + α(用含$\alpha$的代数式表示).

答案： 60° + α 提示:连接OD，OB，则OD⊥BC，∠OBD=30°，所以OD=1/2OB。因为E是OP的中点，所以OE=1/2OP。又因为OB=OP，所以OD=OE，所以∠ODE=∠OED=α，所以∠EOD=180° - 2α。因为∠BOD=60°，所以∠EOB=∠EOD - ∠BOD=120° - 2α。又因为OB=OP，所以∠P=∠OBP=1/2(180° - ∠EOB)=30° + α。所以∠PBC=∠OBP+∠OBC=30° + α+30°=60° + α。

8. 如图,在$\triangle ABC$中,$\angle ABC= 90^\circ,AB= CB= 3$,D为直线BC上一动点,点P是$\triangle CAD$的外心.当点D在直线BC上从一个位置运动到另一个位置时,点P恰好在$\triangle ABC$的内部,则点P运动的最大距离为______$\frac{3\sqrt{2}}{2}$.

答案： 3√2/2 提示:过点B作BE⊥AC于点E。因为点P是△CAD的外心，所以点P在线段AC的垂直平分线上随点D的运动而运动。因为点P恰好在△ABC的内部，所以BE为点P运动的最长路径，且BE=1/2AC。因为AC=√(AB² + BC²)=3√2，所以点P运动的最大距离为3√2/2。

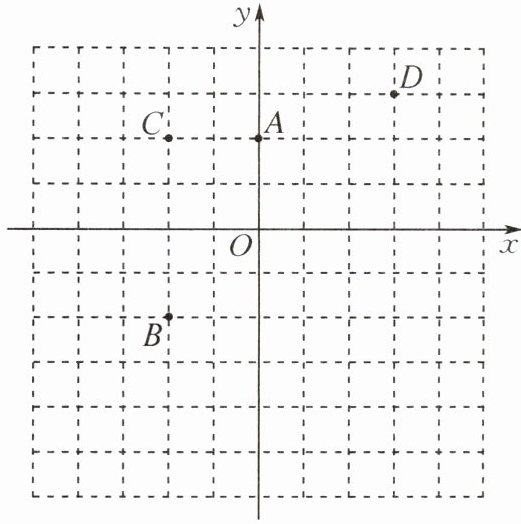
9. (常州市期中)如图,平面直角坐标系中有4个点:A(0,2),B(-2,-2),C(-2,2),D(3,3).
(1)在正方形网格中画出$\triangle ABC的外接圆\odot M$,并写出圆心M的坐标.
(2)在(1)中情况下,若EF是$\odot M$的一条长为4的弦,G为弦EF的中点,求DG的最大值.

答案：

(1) 如图所示，⊙M即为所求，点M(-1,0)。

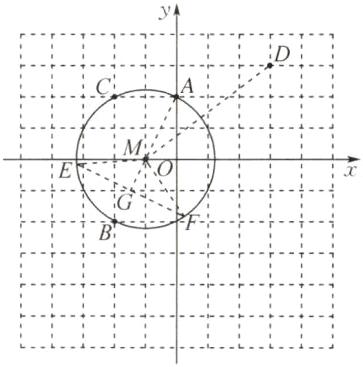
(2) DG的最大值为6。