《2025年小题狂做九年级数学上册苏科版巅峰版》

1. (连云港市中考)如图是由 16 个相同的小正方形和 4 个相同的大正方形组成的图形,在这个图形内任取一点 P,则点 P 落在阴影部分的概率为 (B)
A.$\frac{5}{8}$
B.$\frac{13}{50}$
C.$\frac{13}{32}$
D.$\frac{5}{16}$

答案： B 提示:设16个相同的小正方形的边长为a,则4个相同的大正方形的边长为1.5a，所以点P落在阴影部分的概率为$\frac{2a^{2}+2×(1.5a)^{2}}{16a^{2}+4×(1.5a)^{2}}=\frac{13}{50}$.

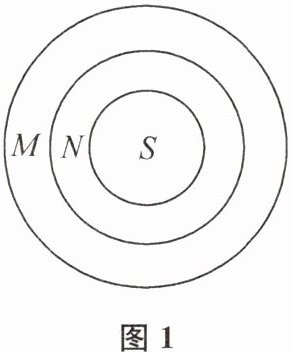
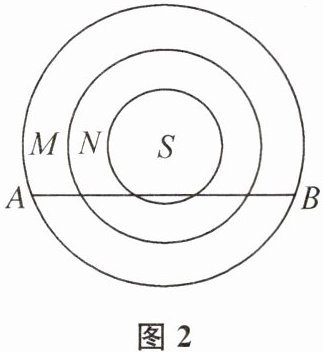
2. 如图1,一只圆形平盘被同心圆划成 M,N,S 三个区域,随机向平盘中撒一把豆子,计算落在 M,N,S 三个区域的豆子数的比.多次重复这个试验,发现落入三个区域的豆子数的比显示出一定的稳定性,总在三个区域的面积之比附近摆动.如图 2,将一根筷子放在该盘中 AB 位置,发现三个圆弧刚好将 AB 五等分.我们把豆子落入三个区域的概率分别记作 P(M),P(N),P(S),已知 $P(S)= \frac{1}{5}$,则 P(M)等于 ( )



A.$\frac{8}{15}$
B.$\frac{2}{5}$
C.$\frac{4}{15}$
D.$\frac{1}{5}$

答案：
A 提示:如图,设小圆的半径为r,则大圆的半径为$\sqrt{5}r$.设$AB = 10a$,$AE = 5a$,$CE = 3a$,$DE = a$,所以$OE^{2}=(\sqrt{5}r)^{2}-(5a)^{2}=r^{2}-a^{2}=OC^{2}-(3a)^{2}$,解得$r^{2}=6a^{2}$,$OC^{2}=14a^{2}$,所以M部分面积与整个圆面积的比为$\frac{5πr^{2}-14πa^{2}}{5πr^{2}}=\frac{16}{30}=\frac{8}{15}$,所以$P(M)=\frac{8}{15}$.
　　　　　　

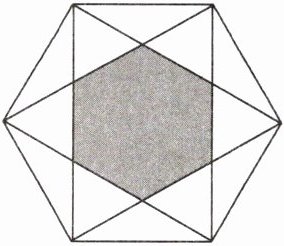
3. 连接正六边形不相邻的两个顶点,并将中间的六边形涂成灰色,制成如图所示的镖盘.将一枚飞镖任意投掷到镖盘上,飞镖落在灰色区域的概率为 ( )


A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{\sqrt{3}}{3}$

答案：
B 提示:如图,设$S_{△ABC}=a$,则$S_{灰色区域}=6a$,$S_{正六边形}=18a$.所以飞镖落在灰色区域的概率为$\frac{6a}{18a}=\frac{1}{3}$.
　　　　　　

4. 一个圆形转盘的半径为 2 cm,现将转盘分成若干个扇形,并分别相间地涂上红、黄两种颜色.转盘转动 10 000 次,指针指向红色部分的有 2 500 次,则转盘上黄色部分的面积大约是$3πcm^{2}$.

答案： $3πcm^{2}$

5. 如图,在$\triangle ABC$中,D,E,F 分别为边 AB,AC,BC 的中点,P,M,N 分别为 DE,DF,EF 的中点.若随机向$\triangle ABC$内投一粒米,则米粒落在图中阴影部分的概率为$\frac{1}{16}$.

答案： $\frac{1}{16}$

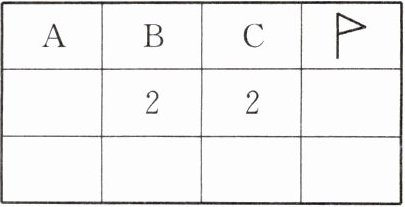
6. 如图是扫雷游戏的一部分(说明：图中数字2表示在以该数字为中心的8个方格中有2个地雷).小旗表示该方格已被探明有地雷,现在还剩下 A,B,C 三个方格未被探明,其他地方为安全区(包括有数字的方格).
(1)现在还剩下几个地雷？
2
(2)A,B,C 三个方格中有地雷的概率分别是多大？
$P(A有地雷)=1$，$P(B有地雷)=\frac{1}{2}$，$P(C有地雷)=\frac{1}{2}$

答案：
(1) 由于B,C下面标2,说明以它们为中心的8个方格中有2个地雷,而C的右边已经有一个,所以A处有一个地雷,还有一个可能在B或C的位置.所以现在还剩下2个地雷.
(2) 根据
(1),得$P(A有地雷)=1$,$P(B有地雷)=\frac{1}{2}$,$P(C有地雷)=\frac{1}{2}$.