10. 如图,⊙O的半径为2,圆心O到直线l的距离为4.现有一内角为60°的菱形,若此菱形的一边在直线l上,另有两边所在的直线恰好与⊙O相切,则该菱形的边长为______.


答案:
4$\sqrt{3}$或$\frac{4\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{3}$ 提示:①如图1,当⊙O与边AB,AD相切时,过点O作直线l的垂线,交AD于点E,交BC于点F,过点A作直线l的垂线,交BC于点G.根据题意,得EF = OE + OF = 2 + 4 = 6.易证四边形AGFE是矩形,所以AG = EF = 6.又因为∠ABC = 60°,所以AB = 2BG.设BG = x,则AB = 2x.在Rt△ABG中,由勾股定理,得AB² = BG² + AG²,即(2x)² = x² + 6²,解得x = 2$\sqrt{3}$(负值已舍).所以AB = 4$\sqrt{3}$,即菱形的边长为4$\sqrt{3}$.②如图2 - 4,菱形的边长为4$\sqrt{3}$,解法同①.③如图5,当⊙O与边AB的反向延长线,边AD的延长线相切时,过点O作直线l的垂线,交AD的延长线于点E,交直线l于点F,过点A作直线l的垂线,交BC于点G.根据题意,得EF = OF - OE = 4 - 2 = 2.易证四边形AGFE是矩形,所以AG = EF = 2.又因为∠ABC = 60°,所以AB = 2BG.设BG = x,则AB = 2x.在Rt△ABG中,由勾股定理,得AB² = BG² + AG²,即(2x)² = x² + 2²,解得x = $\frac{2\sqrt{3}}{3}$(负值已舍).所以AB = $\frac{4\sqrt{3}}{3}$,即菱形的边长为$\frac{4\sqrt{3}}{3}$.④如图6 - 8,菱形的边长为$\frac{4\sqrt{3}}{3}$,解法同③.⑤如图9,当⊙O与边AB,CD所在的直线相切时,过点O作边CD的垂线,交BA的延长线于点E,交CD于点F,过点A作AG⊥CD于点G.易知四边形AGFE是矩形,所以AG = EF = 4.易得∠ADC = 60°,所以AD = 2DG.设DG = x,则AD = 2x.在Rt△ADG中,由勾股定理,得AG² + DG² = AD²,即4² + x² = (2x)²,解得x = $\frac{4\sqrt{3}}{3}$(负值已舍).所以AD = $\frac{8\sqrt{3}}{3}$,经检验,此时点O到直线l的距离为4,符合题意,故此情况下菱形的边长为$\frac{8\sqrt{3}}{3}$.综上所述,该菱形的边长为4$\sqrt{3}$或$\frac{4\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{3}$.









4$\sqrt{3}$或$\frac{4\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{3}$ 提示:①如图1,当⊙O与边AB,AD相切时,过点O作直线l的垂线,交AD于点E,交BC于点F,过点A作直线l的垂线,交BC于点G.根据题意,得EF = OE + OF = 2 + 4 = 6.易证四边形AGFE是矩形,所以AG = EF = 6.又因为∠ABC = 60°,所以AB = 2BG.设BG = x,则AB = 2x.在Rt△ABG中,由勾股定理,得AB² = BG² + AG²,即(2x)² = x² + 6²,解得x = 2$\sqrt{3}$(负值已舍).所以AB = 4$\sqrt{3}$,即菱形的边长为4$\sqrt{3}$.②如图2 - 4,菱形的边长为4$\sqrt{3}$,解法同①.③如图5,当⊙O与边AB的反向延长线,边AD的延长线相切时,过点O作直线l的垂线,交AD的延长线于点E,交直线l于点F,过点A作直线l的垂线,交BC于点G.根据题意,得EF = OF - OE = 4 - 2 = 2.易证四边形AGFE是矩形,所以AG = EF = 2.又因为∠ABC = 60°,所以AB = 2BG.设BG = x,则AB = 2x.在Rt△ABG中,由勾股定理,得AB² = BG² + AG²,即(2x)² = x² + 2²,解得x = $\frac{2\sqrt{3}}{3}$(负值已舍).所以AB = $\frac{4\sqrt{3}}{3}$,即菱形的边长为$\frac{4\sqrt{3}}{3}$.④如图6 - 8,菱形的边长为$\frac{4\sqrt{3}}{3}$,解法同③.⑤如图9,当⊙O与边AB,CD所在的直线相切时,过点O作边CD的垂线,交BA的延长线于点E,交CD于点F,过点A作AG⊥CD于点G.易知四边形AGFE是矩形,所以AG = EF = 4.易得∠ADC = 60°,所以AD = 2DG.设DG = x,则AD = 2x.在Rt△ADG中,由勾股定理,得AG² + DG² = AD²,即4² + x² = (2x)²,解得x = $\frac{4\sqrt{3}}{3}$(负值已舍).所以AD = $\frac{8\sqrt{3}}{3}$,经检验,此时点O到直线l的距离为4,符合题意,故此情况下菱形的边长为$\frac{8\sqrt{3}}{3}$.综上所述,该菱形的边长为4$\sqrt{3}$或$\frac{4\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{3}$.









11. 定义:有一个角是其对角一半的圆内接四边形叫作“圆美四边形”,这个角叫作“美角”.
(1)如图1,若四边形ABCD是“圆美四边形”,求“美角”∠A的度数.
(2)在(1)的条件下,已知⊙O的半径为5.
①求BD的长;
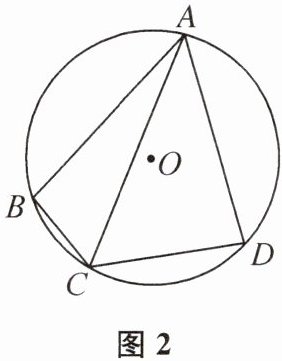
②如图2,在四边形ABCD中,若CA平分∠BCD,求BC+CD的最大值.
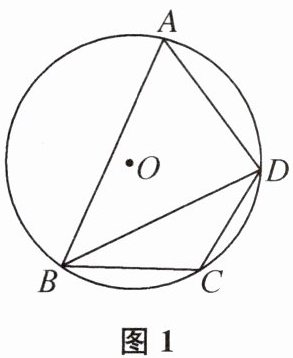
(1)如图1,若四边形ABCD是“圆美四边形”,求“美角”∠A的度数.
(2)在(1)的条件下,已知⊙O的半径为5.
①求BD的长;
②如图2,在四边形ABCD中,若CA平分∠BCD,求BC+CD的最大值.


答案:
(1)由题意,得∠A = $\frac{1}{2}$∠C.又因为∠A + ∠C = 180°,所以∠A = 60°.
(2)①连接DO并延长,交⊙O于点E,连接BE,则∠E = ∠A = 60°.因为DE是⊙O的直径,所以DE = 10,∠DBE = 90°.所以∠BDE = 30°,所以BE = $\frac{1}{2}$DE = 5.在Rt△DBE中,由勾股定理,得BD = $\sqrt{DE² - BE²}$ = 5$\sqrt{3}$.
②连接BD,延长CB到点E,使得EB = CD,连接AE.由
(1)可知∠BAD = 60°,所以∠BCD = 120°.因为CA平分∠BCD,所以∠ACD = ∠ACB = 60°,可得∠ABD = ∠ACD = 60°,∠ADB = ∠ACB = 60°.所以△ABD为等边三角形,所以AB = AD.易证△ACD≌△AEB,所以∠E = ∠ACD = 60°,∠EAB = ∠CAD.所以∠EAC = ∠EAB + ∠BAC = ∠CAD + ∠BAC = 60°.所以△ACE为等边三角形,所以AC = CE.所以BC + CD = BC + EB = CE = AC.因为A为定点,而C为$\overset{\frown}{BD}$上的动点,所以AC的最大值为⊙O的直径,所以BC + CD的最大值为10.
(1)由题意,得∠A = $\frac{1}{2}$∠C.又因为∠A + ∠C = 180°,所以∠A = 60°.
(2)①连接DO并延长,交⊙O于点E,连接BE,则∠E = ∠A = 60°.因为DE是⊙O的直径,所以DE = 10,∠DBE = 90°.所以∠BDE = 30°,所以BE = $\frac{1}{2}$DE = 5.在Rt△DBE中,由勾股定理,得BD = $\sqrt{DE² - BE²}$ = 5$\sqrt{3}$.
②连接BD,延长CB到点E,使得EB = CD,连接AE.由
(1)可知∠BAD = 60°,所以∠BCD = 120°.因为CA平分∠BCD,所以∠ACD = ∠ACB = 60°,可得∠ABD = ∠ACD = 60°,∠ADB = ∠ACB = 60°.所以△ABD为等边三角形,所以AB = AD.易证△ACD≌△AEB,所以∠E = ∠ACD = 60°,∠EAB = ∠CAD.所以∠EAC = ∠EAB + ∠BAC = ∠CAD + ∠BAC = 60°.所以△ACE为等边三角形,所以AC = CE.所以BC + CD = BC + EB = CE = AC.因为A为定点,而C为$\overset{\frown}{BD}$上的动点,所以AC的最大值为⊙O的直径,所以BC + CD的最大值为10.
12. 在△ABC和△ADE中,∠BAC= ∠DAE= 90°,AB= AC,AD= AE,固定△ABC,将△ADE绕点A旋转一周,连接BE,CD相交于点H,经过C,E,H三点作⊙O.
(1)如图1,求证:CE是⊙O的直径.
(2)若AB= 3,AD= 2√2,连接BD,在△ADE的旋转过程中:
①若点A恰好是△CEH的内心,如图2,求BD的长;
②当∠ABD最大时,△ACE的面积为______
(1)如图1,求证:CE是⊙O的直径.
(2)若AB= 3,AD= 2√2,连接BD,在△ADE的旋转过程中:
①若点A恰好是△CEH的内心,如图2,求BD的长;
②当∠ABD最大时,△ACE的面积为______
$\sqrt{2}$
.
答案:
(1)证明:易证△CAD≌△BAE,所以∠ACD = ∠ABE.所以∠CHE = ∠ABC + ∠ABE + ∠BCH = ∠ABC + ∠ACD + ∠BCH = ∠ABC + ∠ACB = 180° - ∠BAC = 90°.所以CE是⊙O的直径.
(2)解:①由
(1)可知,∠HCE + ∠HEC = 90°.因为点A是△CEH的内心,所以∠ACE + ∠AEC = $\frac{1}{2}$(∠HCE + ∠HEC) = 45°,所以∠CAE = 180° - (∠ACE + ∠AEC) = 135°.因为∠CAB = ∠DAE = 90°,所以∠BAD = 360° - ∠CAB - ∠DAE - ∠CAE = 45°.过点D作DG⊥AB于点G,则AG = DG = $\frac{\sqrt{2}}{2}$AD = 2.所以BG = AB - AG = 1.所以BD = $\sqrt{DG² + BG²}$ = $\sqrt{5}$.
②$\sqrt{2}$ 提示:以点A为圆心,AD的长为半径作⊙A.当BD与⊙A相切时,∠ABD最大,此时BD = $\sqrt{AB² - AD²}$ = 1.过点C作CP⊥AE,交EA的延长线于点P.因为∠CAP + ∠CAE = 180°,∠BAD + ∠CAE = 180°,所以∠CAP = ∠BAD.又因为∠CPA = ∠BDA = 90°,AC = AB,所以△ACP≌△ABD,所以CP = BD = 1.所以S△ACE = $\frac{1}{2}$AE·CP = $\frac{1}{2}$×2$\sqrt{2}$×1 = $\sqrt{2}$.
(1)证明:易证△CAD≌△BAE,所以∠ACD = ∠ABE.所以∠CHE = ∠ABC + ∠ABE + ∠BCH = ∠ABC + ∠ACD + ∠BCH = ∠ABC + ∠ACB = 180° - ∠BAC = 90°.所以CE是⊙O的直径.
(2)解:①由
(1)可知,∠HCE + ∠HEC = 90°.因为点A是△CEH的内心,所以∠ACE + ∠AEC = $\frac{1}{2}$(∠HCE + ∠HEC) = 45°,所以∠CAE = 180° - (∠ACE + ∠AEC) = 135°.因为∠CAB = ∠DAE = 90°,所以∠BAD = 360° - ∠CAB - ∠DAE - ∠CAE = 45°.过点D作DG⊥AB于点G,则AG = DG = $\frac{\sqrt{2}}{2}$AD = 2.所以BG = AB - AG = 1.所以BD = $\sqrt{DG² + BG²}$ = $\sqrt{5}$.
②$\sqrt{2}$ 提示:以点A为圆心,AD的长为半径作⊙A.当BD与⊙A相切时,∠ABD最大,此时BD = $\sqrt{AB² - AD²}$ = 1.过点C作CP⊥AE,交EA的延长线于点P.因为∠CAP + ∠CAE = 180°,∠BAD + ∠CAE = 180°,所以∠CAP = ∠BAD.又因为∠CPA = ∠BDA = 90°,AC = AB,所以△ACP≌△ABD,所以CP = BD = 1.所以S△ACE = $\frac{1}{2}$AE·CP = $\frac{1}{2}$×2$\sqrt{2}$×1 = $\sqrt{2}$.
查看更多完整答案,请扫码查看


