《2025年小题狂做九年级数学上册苏科版巅峰版》

1. 如图,点A,B,C在⊙O上,∠AOC= 90°,AB= √2,BC= 1,则⊙O的半径为(C)
A.√3
B.√5/2
C.√10/2
D.(√2+1)/2

答案： C 提示:过点A作AE⊥CB，交CB的延长线于点E，连接AC.易知∠OAB = ∠OBA，∠OBC = ∠OCB.又因为∠AOC = 90°，所以∠ABC = $\frac{1}{2}$×(360° - 90°) = 135°，所以∠ABE = 45°.又因为∠E = 90°，AB = $\sqrt{2}$，所以AE = EB = 1.易得EC = 2.所以AC = $\sqrt{AE² + EC²}$ = $\sqrt{5}$.易得OA = OC = $\frac{\sqrt{2}}{2}$AC = $\frac{\sqrt{10}}{2}$，即⊙O的半径为$\frac{\sqrt{10}}{2}$.

2. 如图,在正方形ABCD中,AB= 4,以点B为圆心,1为半径作⊙B,点P在⊙B上移动,连接AP,将AP绕点A逆时针旋转90°至AP',连接BP'.在点P的移动过程中,BP'长的最小值为(A)
A.4√2-1
B.4√2
C.4√3
D.3

答案： A 提示:连接DP'，BP.易证△ADP'≌△ABP，所以DP' = BP = 1.所以点P'在以点D为圆心，1为半径的⊙D上运动.连接BD，当点D，P'，B依次共线时，BP'的长度最小，最小值为BD - DP'.在Rt△ABD中，AB = AD = 4，由勾股定理，得BD = 4$\sqrt{2}$.所以BP'长的最小值为BD - DP' = 4$\sqrt{2}$ - 1.

3. (泰州市靖江市模拟)如图,在由等边三角形、正方形、圆组成的轴对称图案中,等边三角形的面积与三个正方形的面积之和的比值为(A)
A.√3/2
B.1
C.√3
D.3√3/2

答案： A 提示:设圆的圆心为O.根据题意，可知等边三角形的中心以及三个正方形的公共顶点即为点O，过点A作AD⊥BC于点D，则AD必过点O.连接OB.易得∠OBD = 30°，所以AO = BO = 2OD.设△ABC的边长为2x，则BD = x，AD = $\sqrt{3}$x，OD = $\frac{\sqrt{3}}{3}$x.易得正方形的边长为$\frac{\sqrt{6}}{3}$x，所以正方形的面积为$\frac{2}{3}$x²，所以三个正方形的面积之和为2x².易求得△ABC的面积为$\frac{1}{2}$×2x·$\sqrt{3}$x = $\sqrt{3}$x².所以等边三角形的面积与三个正方形的面积之和的比值为$\frac{\sqrt{3}}{2}$.

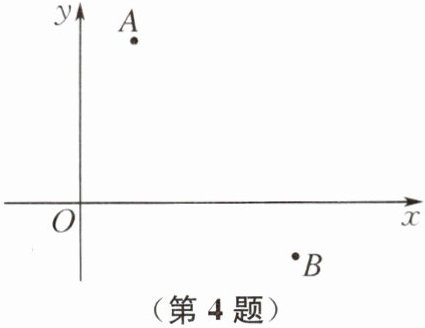
4. 如图,已知点A(2,6),B(8,-2),C为坐标轴上一点,且△ABC是直角三角形,则满足条件的点C有( )

A.6个
B.7个
C.8个
D.9个

答案：
B 提示:如图，分三种情况讨论:①当A为直角顶点时，过点A作AC⊥AB，交x轴于点C₁，交y轴于点C₂，此时满足题意的点为C₁，C₂;②当B为直角顶点时，过点B作BC⊥AB，交x轴于点C₃，交y轴于点C₄，此时满足题意的点为C₃，C₄;③当C为直角顶点时，以AB为直径作圆，由点A(2，6)，B(8， - 2)可得，圆心的坐标为(5，2)，AB = $\sqrt{(8 - 2)² + (- 2 - 6)²}$ = 10，所以此圆的半径为5，所以此圆与y轴相切，与x轴相交，即此圆与y轴有1个交点，与x轴有2个交点，此时满足题意的点为C₅，C₆，C₇.综上所述，满足条件的点C有7个.

5. 如图,扇形OAB的圆心角为直角,边长为3的正方形OCDE的顶点C,E,D分别在OA,OB及⌢AB上,过点A作AF⊥ED,交ED的延长线于点F,则图中阴影部分的面积为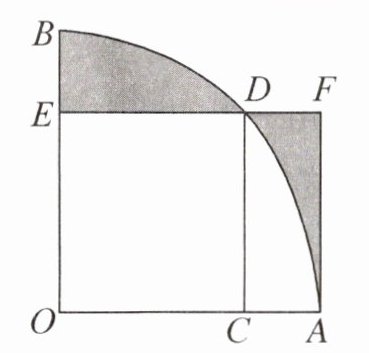9$\sqrt{2}$ - 9.

答案： 9$\sqrt{2}$ - 9

6. 若一个圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图所对应的扇形的圆心角为180°.

答案： 180°

7. 如图,⊙O是△ABC的外接圆,∠BAC= 45°,AD⊥BC于点D,延长AD交⊙O于点E.若BD= 4,CD= 1,则AD的长是______$\frac{\sqrt{41} + 5}{2}$.

答案： $\frac{\sqrt{41} + 5}{2}$ 提示:连接OA，过点O分别作OF⊥BC于点F，OG⊥AE于点G.易知△OBC为等腰直角三角形，BC = BD + CD = 5，所以OA = OB = OC = $\frac{5\sqrt{2}}{2}$，GD = OF = BF = $\frac{5}{2}$，所以OG = DF = BD - BF = $\frac{3}{2}$.在Rt△AGO中，由勾股定理，得AG = $\sqrt{OA² - OG²}$ = $\frac{\sqrt{41}}{2}$.所以AD = AG + GD = $\frac{\sqrt{41} + 5}{2}$.

8. 如图,在平面直角坐标系xOy中,P是直线y= 3上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ长的最小值为______2$\sqrt{2}$.

答案： 2$\sqrt{2}$ 提示:连接PQ，OP.因为直线OQ切⊙P于点Q，所以PQ⊥OQ.在Rt△OPQ中，由勾股定理，得OQ = $\sqrt{OP² - PQ²}$ = $\sqrt{OP² - 1}$.当OP的值最小时，OQ的值最小.当OP⊥直线y = 3时，OP取得最小值，为3，所以OQ长的最小值为$\sqrt{OP² - 1}$ = $\sqrt{3² - 1}$ = 2$\sqrt{2}$.

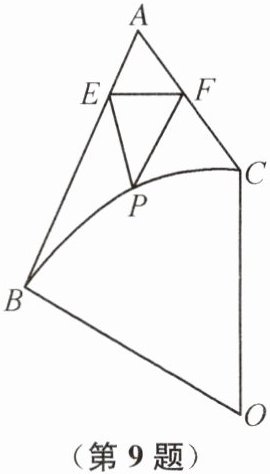
9. 如图,AB= 6,AC= 3,∠BAC= 60°,⌢BC为⊙O上的一段弧,且∠BOC= 60°,分别在⌢BC、线段AB和AC上选取点P,E,F,则PE+EF+PF的最小值为______.

答案：
3$\sqrt{21}$ - 9 提示:分别作点P关于AB的对称点M，关于AC的对称点N，连接EM，PM，FN，PN.由对称性可知，PE + EF + PF = EM + EF + FN，所以当M，E，F，N四点共线时，PE + EF + PF的值最小，最小值为线段MN的长，如图所示.连接AM，AP，AN.由对称性可知，AP = AM = AN，∠BAM = ∠BAP，∠CAP = ∠CAN.又因为∠BAC = 60°，所以∠MAN = 120°.所以易得MN = $\sqrt{3}$AM = $\sqrt{3}$AP，所以当AP的值最小时，MN的值最小.取AB的中点J，连接BC，OA，CJ.因为AB = 6，AC = 3，所以JA = JB = 3 = AC.又因为∠JAC = 60°，所以△JAC是等边三角形.所以JC = JA = JB，∠AJC = ∠ACJ = 60°，所以∠JBC = ∠JCB = 30°.所以∠ACB = 90°，所以BC = $\sqrt{AB² - AC²}$ = 3$\sqrt{3}$.又因为∠BOC = 60°，OB = OC，所以△OBC是等边三角形，所以OB = OC = BC = 3$\sqrt{3}$，∠OBC = 60°.所以∠ABO = 90°，所以OA = $\sqrt{AB² + OB²}$ = 3$\sqrt{7}$.连接OP，则OP = OB = 3$\sqrt{3}$.易知AP ≥ OA - OP，所以当点P在线段OA上时，AP的值最小，最小值为3$\sqrt{7}$ - 3$\sqrt{3}$.所以PE + EF + PF的最小值为$\sqrt{3}$×(3$\sqrt{7}$ - 3$\sqrt{3}$) = 3$\sqrt{21}$ - 9.