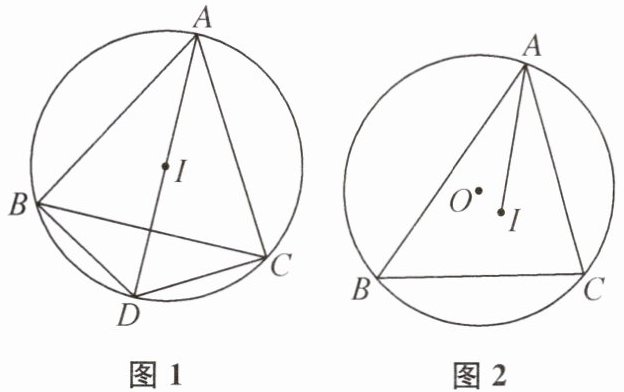
10. (1)如图 1,I 为△ABC 内一点,AI 的延长线交△ABC 的外接圆于点 D.若 DB= DI= DC,求证:I 为△ABC 的内心.
(2)如图 2,⊙O 的半径长为 5,弦 BC= 8,动点 A 在$\widehat{BAC}$上(不与点 B,C 重合),点 I 是△ABC 的内心.
①点 I 到⊙O 上某点的距离始终不变,请用无刻度的直尺找出该点;
②AI 长的最大值为______.
]
(2)如图 2,⊙O 的半径长为 5,弦 BC= 8,动点 A 在$\widehat{BAC}$上(不与点 B,C 重合),点 I 是△ABC 的内心.
①点 I 到⊙O 上某点的距离始终不变,请用无刻度的直尺找出该点;
②AI 长的最大值为______.
]

答案:
(1)证明:如图1,连接BI。因为BD = CD,所以$\overset{\frown}{BD}$ = $\overset{\frown}{CD}$,所以∠BAD = ∠DBC = ∠CAD,所以AD平分∠BAC。因为BD = DI,所以∠IBD = ∠BID = ∠BAD + ∠ABI。又因为∠IBD = ∠DBC + ∠CBI,∠DBC = ∠BAD,所以∠ABI = ∠CBI。所以BI平分∠ABC,所以点I为△ABC的内心。

(2)解:①如图2,作AI的延长线交⊙O于点D,点D即为所求。 提示:连接BI,BD。因为点I是△ABC的内心,所以∠BAD = ∠CAD,∠ABI = ∠CBI,所以BD = CD,所以D为$\overset{\frown}{BC}$的中点,所以∠CBD = ∠CAD = ∠BAD。因为∠BID = ∠BAD + ∠ABI,∠DBI = ∠CBD + ∠CBI,所以∠BID = ∠DBI。所以DI = DB = CD,所以DI是一个定值。


②10 - 2$\sqrt{5}$ 提示:因为AI = AD - DI,DI = BD,所以AI = AD - DB,所以当AD取最大值时,AI取得最大值,所以当AD为⊙O的直径时,AI取得最大值。如图3,设AD交BC于点M,连接OB。因为点I是△ABC的内心,所以∠BAD = ∠CAD,所以$\overset{\frown}{BD}$ = $\overset{\frown}{CD}$。因为AD是⊙O的直径,所以AD⊥BC,BM = CM = $\frac{1}{2}$BC = 4,所以∠AMB = 90°。因为⊙O的半径长为5,所以OB = OD = 5,AD = 10。所以OM = $\sqrt{OB^{2}-BM^{2}}$ = 3,所以MD = OD - OM = 2,所以BD = $\sqrt{BM^{2}+MD^{2}}$ = 2$\sqrt{5}$。所以AI = AD - BD = 10 - 2$\sqrt{5}$,所以AI长的最大值为10 - 2$\sqrt{5}$。
(1)证明:如图1,连接BI。因为BD = CD,所以$\overset{\frown}{BD}$ = $\overset{\frown}{CD}$,所以∠BAD = ∠DBC = ∠CAD,所以AD平分∠BAC。因为BD = DI,所以∠IBD = ∠BID = ∠BAD + ∠ABI。又因为∠IBD = ∠DBC + ∠CBI,∠DBC = ∠BAD,所以∠ABI = ∠CBI。所以BI平分∠ABC,所以点I为△ABC的内心。

(2)解:①如图2,作AI的延长线交⊙O于点D,点D即为所求。 提示:连接BI,BD。因为点I是△ABC的内心,所以∠BAD = ∠CAD,∠ABI = ∠CBI,所以BD = CD,所以D为$\overset{\frown}{BC}$的中点,所以∠CBD = ∠CAD = ∠BAD。因为∠BID = ∠BAD + ∠ABI,∠DBI = ∠CBD + ∠CBI,所以∠BID = ∠DBI。所以DI = DB = CD,所以DI是一个定值。


②10 - 2$\sqrt{5}$ 提示:因为AI = AD - DI,DI = BD,所以AI = AD - DB,所以当AD取最大值时,AI取得最大值,所以当AD为⊙O的直径时,AI取得最大值。如图3,设AD交BC于点M,连接OB。因为点I是△ABC的内心,所以∠BAD = ∠CAD,所以$\overset{\frown}{BD}$ = $\overset{\frown}{CD}$。因为AD是⊙O的直径,所以AD⊥BC,BM = CM = $\frac{1}{2}$BC = 4,所以∠AMB = 90°。因为⊙O的半径长为5,所以OB = OD = 5,AD = 10。所以OM = $\sqrt{OB^{2}-BM^{2}}$ = 3,所以MD = OD - OM = 2,所以BD = $\sqrt{BM^{2}+MD^{2}}$ = 2$\sqrt{5}$。所以AI = AD - BD = 10 - 2$\sqrt{5}$,所以AI长的最大值为10 - 2$\sqrt{5}$。
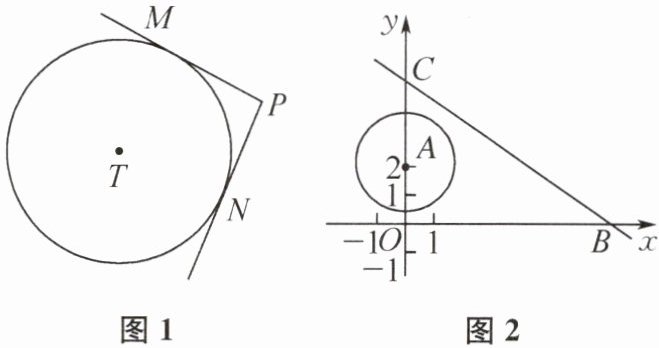
11. 如图 1,在平面内,过⊙T 外一点 P 作它的两条切线,切点分别为 M,N,若∠MPN≥90°,则称 P 为⊙T 的“限角点”.
(1)在平面直角坐标系 xOy 中,当⊙O 的半径为 1 时,在①点$P_1(1,0)$,②点$P_2(-1,\frac{1}{2})$,③点$P_3(-1,-1)$,④点$P_4(2,-1)$中,属于⊙O 的“限角点”的是______(填序号).
(2)如图 2,⊙A 的半径为$\sqrt{2}$,圆心坐标为(0,2),直线$l:y= -\frac{3}{4}x+b$分别交坐标轴于点 B,C.若直线 l 上有且只有一个⊙A 的“限角点”,求 b 的值.
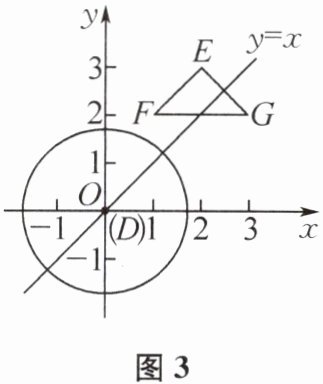
(3)如图 3,点 E(2,3),F(1,2),G(3,2),⊙D 的半径为$\sqrt{2}$,圆心 D 从原点 O 出发,以每秒$\sqrt{2}个单位长度的速度沿直线l':y= x$向上运动.若△EFG 的边上存在⊙D 的“限角点”,请直接写出运动时间 t(s)的取值范围.
]
(1)在平面直角坐标系 xOy 中,当⊙O 的半径为 1 时,在①点$P_1(1,0)$,②点$P_2(-1,\frac{1}{2})$,③点$P_3(-1,-1)$,④点$P_4(2,-1)$中,属于⊙O 的“限角点”的是______(填序号).
(2)如图 2,⊙A 的半径为$\sqrt{2}$,圆心坐标为(0,2),直线$l:y= -\frac{3}{4}x+b$分别交坐标轴于点 B,C.若直线 l 上有且只有一个⊙A 的“限角点”,求 b 的值.
(3)如图 3,点 E(2,3),F(1,2),G(3,2),⊙D 的半径为$\sqrt{2}$,圆心 D 从原点 O 出发,以每秒$\sqrt{2}个单位长度的速度沿直线l':y= x$向上运动.若△EFG 的边上存在⊙D 的“限角点”,请直接写出运动时间 t(s)的取值范围.
]


答案:
解:
(1)②③
(2)因为⊙A的半径为$\sqrt{2}$,所以当P为⊙A的“限角点”时,$\sqrt{2}$ < AP ≤ 2。若直线l上有且只有一个⊙A的“限角点”P,则AP = 2,且AP⊥BC。易得点C(0, b),B($\frac{4}{3}$b, 0)。设点P(m, -$\frac{3}{4}$m + b)。如图1,过点P作PD⊥OC于点D。易得AC = |b - 2|,CD = $\frac{3}{4}$|m|,PD = |m|,所以PC = $\sqrt{CD^{2}+PD^{2}}$ = |$\frac{5}{4}$m|。因为$S_{\triangle APC}=\frac{1}{2}AC\cdot PD=\frac{1}{2}AP\cdot PC$,所以$b_1=\frac{9}{2}$,$b_2=-\frac{1}{2}$,即b的值为$\frac{9}{2}$或 -$\frac{1}{2}$。


(3)t的取值范围是$\frac{3 - \sqrt{7}}{2}$ ≤ t < $\frac{5 - \sqrt{3}}{2}$或$\frac{3 + \sqrt{3}}{2}$ < t ≤ $\sqrt{2}+\frac{5}{2}$。 提示:如图2,因为圆心D从原点O出发,以每秒$\sqrt{2}$个单位长度的速度沿直线l'移动t s时,所以OD = $\sqrt{2}$t,移动后点D的坐标为(t, t)。设△EFG边上的P是⊙D的“限角点”,则$\sqrt{2}$ < PD ≤ 2。在⊙D移动的过程中,当DF = 2时,$(t - 1)^{2}+(t - 2)^{2}=4$,解得$t_1=\frac{3 - \sqrt{7}}{2}$,$t_2=\frac{3 + \sqrt{7}}{2}$。当$t=\frac{3 - \sqrt{7}}{2}$时,△EFG边上开始出现⊙D的“限角点”。当⊙D移动到点E在圆上时,DE = $\sqrt{2}$,即$(t - 2)^{2}+(t - 3)^{2}=2$,解得$t_1=\frac{5 + \sqrt{3}}{2}$,$t_2=\frac{5 - \sqrt{3}}{2}$。易知当$\frac{3 - \sqrt{7}}{2}$ ≤ t < $\frac{5 - \sqrt{3}}{2}$时,△EFG边上存在⊙D的“限角点”。当⊙D再次移动,直到点F在圆上时,DF = $\sqrt{2}$,即$(t - 2)^{2}+(t - 1)^{2}=2$,解得$t_1=\frac{3 + \sqrt{3}}{2}$,$t_2=\frac{3 - \sqrt{3}}{2}$。当$t=\frac{3 + \sqrt{3}}{2}$时,△EFG三边上又将开始出现⊙D的“限角点”。易得直线EG的函数表达式为y = -x + 5,直线y = x与直线EG的交点H($\frac{5}{2}$,$\frac{5}{2}$)。当DH = 2时,$2(t - \frac{5}{2})^{2}=4$,解得$t_1=\sqrt{2}+\frac{5}{2}$,$t_2=-\sqrt{2}+\frac{5}{2}$,所以当$t=\sqrt{2}+\frac{5}{2}$时,△EFG边上存在⊙D的“限角点”。易知当$\frac{3 + \sqrt{3}}{2}$ < t ≤ $\sqrt{2}+\frac{5}{2}$时,△EFG边上存在⊙D的“限角点”。
解:
(1)②③
(2)因为⊙A的半径为$\sqrt{2}$,所以当P为⊙A的“限角点”时,$\sqrt{2}$ < AP ≤ 2。若直线l上有且只有一个⊙A的“限角点”P,则AP = 2,且AP⊥BC。易得点C(0, b),B($\frac{4}{3}$b, 0)。设点P(m, -$\frac{3}{4}$m + b)。如图1,过点P作PD⊥OC于点D。易得AC = |b - 2|,CD = $\frac{3}{4}$|m|,PD = |m|,所以PC = $\sqrt{CD^{2}+PD^{2}}$ = |$\frac{5}{4}$m|。因为$S_{\triangle APC}=\frac{1}{2}AC\cdot PD=\frac{1}{2}AP\cdot PC$,所以$b_1=\frac{9}{2}$,$b_2=-\frac{1}{2}$,即b的值为$\frac{9}{2}$或 -$\frac{1}{2}$。


(3)t的取值范围是$\frac{3 - \sqrt{7}}{2}$ ≤ t < $\frac{5 - \sqrt{3}}{2}$或$\frac{3 + \sqrt{3}}{2}$ < t ≤ $\sqrt{2}+\frac{5}{2}$。 提示:如图2,因为圆心D从原点O出发,以每秒$\sqrt{2}$个单位长度的速度沿直线l'移动t s时,所以OD = $\sqrt{2}$t,移动后点D的坐标为(t, t)。设△EFG边上的P是⊙D的“限角点”,则$\sqrt{2}$ < PD ≤ 2。在⊙D移动的过程中,当DF = 2时,$(t - 1)^{2}+(t - 2)^{2}=4$,解得$t_1=\frac{3 - \sqrt{7}}{2}$,$t_2=\frac{3 + \sqrt{7}}{2}$。当$t=\frac{3 - \sqrt{7}}{2}$时,△EFG边上开始出现⊙D的“限角点”。当⊙D移动到点E在圆上时,DE = $\sqrt{2}$,即$(t - 2)^{2}+(t - 3)^{2}=2$,解得$t_1=\frac{5 + \sqrt{3}}{2}$,$t_2=\frac{5 - \sqrt{3}}{2}$。易知当$\frac{3 - \sqrt{7}}{2}$ ≤ t < $\frac{5 - \sqrt{3}}{2}$时,△EFG边上存在⊙D的“限角点”。当⊙D再次移动,直到点F在圆上时,DF = $\sqrt{2}$,即$(t - 2)^{2}+(t - 1)^{2}=2$,解得$t_1=\frac{3 + \sqrt{3}}{2}$,$t_2=\frac{3 - \sqrt{3}}{2}$。当$t=\frac{3 + \sqrt{3}}{2}$时,△EFG三边上又将开始出现⊙D的“限角点”。易得直线EG的函数表达式为y = -x + 5,直线y = x与直线EG的交点H($\frac{5}{2}$,$\frac{5}{2}$)。当DH = 2时,$2(t - \frac{5}{2})^{2}=4$,解得$t_1=\sqrt{2}+\frac{5}{2}$,$t_2=-\sqrt{2}+\frac{5}{2}$,所以当$t=\sqrt{2}+\frac{5}{2}$时,△EFG边上存在⊙D的“限角点”。易知当$\frac{3 + \sqrt{3}}{2}$ < t ≤ $\sqrt{2}+\frac{5}{2}$时,△EFG边上存在⊙D的“限角点”。
查看更多完整答案,请扫码查看


