《2025年小题狂做九年级数学上册苏科版巅峰版》

10. 有5个正整数$a_{1},a_{2},a_{3},a_{4},a_{5}$,某数学兴趣小组的同学探索同时满足以下3个条件的数:①$a_{1},a_{2},a_{3}$是三个连续偶数($a_{1}＜a_{2}＜a_{3}$);②$a_{4},a_{5}$是两个连续奇数($a_{4}＜a_{5}$);③$a_{1}+a_{2}+a_{3}= a_{4}+a_{5}$.该小组成员分别得到一个结论:
甲:取$a_{2}= 6$,5个正整数不满足上述3个条件;
乙:取$a_{2}= 12$,5个正整数满足上述3个条件;
丙:当$a_{2}$满足"$a_{2}$是4的倍数"时,5个正整数满足上述3个条件;
丁:5个正整数$a_{1},a_{2},a_{3},a_{4},a_{5}$满足上述3个条件,则$a_{5}= 3k+4$(k为正奇数);
戊:5个正整数满足上述3个条件,则$a_{1},a_{2},a_{3}的平均数与a_{4},a_{5}$的平均数之和是10p(p为正整数).
以上结论正确的个数为 (D)
A.2
B.3
C.4
D.5

答案： D 提示:审题可发现,丁的结论更具一般性,所以考虑从丁的结论出发,再进行推理.设$a_{1}=2k$(k是正整数),由条件①,得$a_{2}=2k+2$,$a_{3}=2k+4$,由条件②,得$a_{4}=a_{5}-2$,$a_{4},a_{5}$是奇数,由条件③,得$2k+2k+2+2k+4=a_{5}+a_{5}-2$,解得$a_{5}=3k+4$,当k是奇数,$3k+4$也是奇数,所以丁的结论正确.不妨设这5个数依次为$2k$,$2k+2$,$2k+4$,$3k+2$,$3k+4$.若$a_{2}=6$,相当于丁的结论中的k满足$2k+2=6$,解得$k=2$,不是奇数,所以甲的结论正确.若$a_{2}=12$,同理,相当于丁的结论中$k=5$,为奇数,所以乙的结论正确.若$a_{2}$是4的倍数,设$a_{2}=4n$(n是正整数),由条件①,得$a_{1}=4n-2$,$a_{3}=4n+2$,由条件②,得$a_{5}=a_{4}+2$,由条件③,得$4n-2+4n+4n+2=a_{4}+a_{4}+2$,解得$a_{4}=6n-1$,$a_{4}$是奇数,符合题意,所以丙的结论正确.易得$a_{1},a_{2},a_{3}$的平均数为$\frac{2k+2k+2+2k+4}{3}=2k+2$,$a_{4},a_{5}$的平均数为$\frac{3k+4+3k+2}{2}=3k+3$,所以$a_{1},a_{2},a_{3}$的平均数与$a_{4},a_{5}$的平均数之和为$2k+2+3k+3=5(k+1)$.因为k是正奇数,所以$5(k+1)$是10的倍数,所以戊的结论正确.

11. 某学校九年级有m个班($5＜m＜15$)参加了一次足球联赛,比赛规则如下:每个班都与其他班级比赛一场,每场比赛中获胜的班级获得2个积分,平局两个班各获得1个积分,输掉比赛不获得积分.已知其中有2个班一共得了17个积分,且剩余其他所有班级积分的平均数为整数,则m的值为 7.

答案： 7 提示:由题意可知,共进行了$\frac{m(m-1)}{2}$场比赛,所以共有$m(m-1)$个积分.因为其中有2个班一共得了17个积分,且剩余其他所有班级积分的平均数为整数,所以$\frac{m(m-1)-17}{m-2}=\frac{m(m-2)+m-17}{m-2}=m+1-\frac{15}{m-2}$为整数.易知$3＜ m-2＜13$,所以当$m-2=5$,即$m=7$时,满足题意,所以参加此次比赛一共有7个班级.

12. 某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班52位同学(不含甲、乙)进行民主测评,结果如图所示:

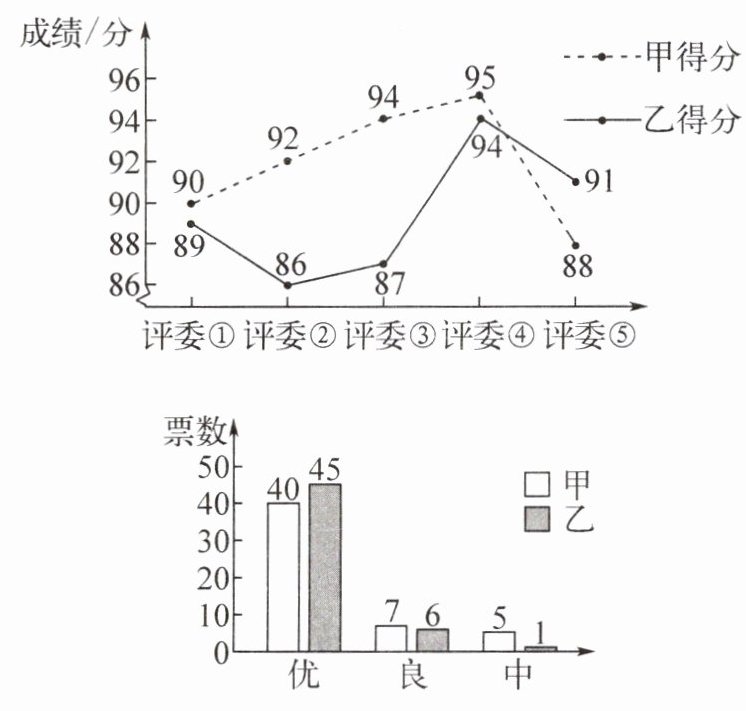
【确定规则】
①个人测评得分$(x_{1})$算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分$(x_{2})$算法:"优"票数$×3+$"良"票数$×2+$"中"票数$×1;$
③综合得分(X)算法:$X= 0.4x_{1}+0.6x_{2}.$
【问题解决】
(1)如果只采用个人测评规则,你认为获胜者是谁.
(2)分别求甲的民主测评得分和乙的民主测评得分.
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?

答案：
(1)如果只采用个人测评规则,你认为获胜者是谁.解:甲的个人测评得分为$\frac{90+92+94}{3}=92$(分),乙的个人测评得分为$\frac{87+89+91}{3}=89$(分).因为$92＞89$,所以获胜者是甲.
(2)分别求甲的民主测评得分和乙的民主测评得分.解:甲的民主测评得分为$40×3+7×2+5×1=139$(分),乙的民主测评得分为$45×3+6×2+1×1=148$(分).
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?解:甲的综合得分为$0.4×92+0.6×139=120.2$(分),乙的综合得分为$0.4×89+0.6×148=124.4$(分).因为$124.4＞120.2$,所以最终当选的是乙.