1. 某篮球队5名场上队员的身高(单位:cm)分别是:184,188,190,192,194.现用1名身高为170 cm的队员换下场上身高为190 cm的队员,与换人前相比,场上队员身高的 (
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
B
)A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
答案:
B
2. 已知一组数据$x_{1},x_{2},x_{3}$的平均数和方差分别为5和2,则数据$x_{1}+1,x_{2}+1,x_{3}+1$的平均数和方差分别是 (
A.5和2
B.6和2
C.5和3
D.6和3
B
)A.5和2
B.6和2
C.5和3
D.6和3
答案:
B
3. 甲、乙、丙、丁四人10次练习的成绩如图所示,从图中可以看出这10次练习平均成绩较高且较稳定的是 (
A.甲
B.乙
C.丙
D.丁
C
)A.甲
B.乙
C.丙
D.丁
答案:
C
4. 对某条道路的长度进行了5次测量,得到5个结果(单位:km):$x_{1}= 104,x_{2}= 101,x_{3}= 102,x_{4}= 104,x_{5}= 103$.如果用$x$作为这条道路长度的近似值,且使得$(x-x_{1})^{2}+(x-x_{2})^{2}+… +(x-x_{5})^{2}$的值最小,那么$x$应选取这5次测量结果的 (
A.中位数
B.众数
C.平均数
D.最小值
C
)A.中位数
B.众数
C.平均数
D.最小值
答案:
C
5. 若一组数据的标准差计算公式是$s= \frac {1}{10}× \sqrt {(1-6)^{2}+(7-6)^{2}+… +(-10-6)^{2}}$,则这组数据的平均数是
6
,共有数据100
个.
答案:
6 100
6. 若一组数据1,2,x,4的众数是1,则这组数据的方差为
1.5
.
答案:
1.5
7. 若数据2,3,5,a的平均数是3,数据3,7,a,b,8的平均数是5,数据a,b,c,9的平均数是5,则数据a,b,c,9的方差是
6.5
.
答案:
6.5
8. 若10个数据的平方和是144,平均数是3,则这组数据的方差是______.
5.4
答案:
5.4 提示:由方差的计算公式,得$s^{2}=\frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+\cdots +(x_{n}-\overline {x})^{2}]=\frac {1}{n}[x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}+n\overline {x}^{2}-2\overline {x}(x_{1}+x_{2}+\cdots +x_{n})]=\frac {1}{n}[x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}+n\overline {x}^{2}-2n\overline {x}^{2}]=\frac {1}{n}[x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}]-\overline {x}^{2}$,所以这组数据的方差是$\frac {144}{10}-3^{2}=5.4.$
9. 已知一组数据$x_{1},x_{2},x_{3},x_{4},x_{5}$的平均数为5,方差为3,则另一组新数据$2x_{1}+1,2x_{2}+1,2x_{3}+1,2x_{4}+1,2x_{5}+1$的平均数、方差分别为
11,12
.
答案:
11,12
10. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩计算了甲成绩的平均数和方差(见小宇的作业).
小宇的作业
解:$\overline {x}_{甲}= \frac {1}{5}× (9+4+7+4+6)= 6$(环),
$s^{2}_{甲}= \frac {1}{5}× [(9-6)^{2}+(4-6)^{2}+(7-6)^{2}+(4-6)^{2}+(6-6)^{2}]$
$=\frac {1}{5}× (9+4+1+4+0)$
$=3.6$(环^2).
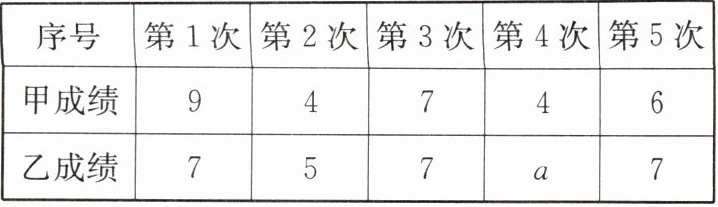
(1) 求a的值和乙的方差$s^{2}_{乙}$.
(2) 请你从平均数和方差的角度分析,谁将被选中?
小宇的作业
解:$\overline {x}_{甲}= \frac {1}{5}× (9+4+7+4+6)= 6$(环),
$s^{2}_{甲}= \frac {1}{5}× [(9-6)^{2}+(4-6)^{2}+(7-6)^{2}+(4-6)^{2}+(6-6)^{2}]$
$=\frac {1}{5}× (9+4+1+4+0)$
$=3.6$(环^2).

(1) 求a的值和乙的方差$s^{2}_{乙}$.
(2) 请你从平均数和方差的角度分析,谁将被选中?
答案:
(1) 因为两人各射了5箭,且总成绩相同,所以$\overline {x}_{乙}=\overline {x}_{甲}=6$环,即$\overline {x}_{乙}=\frac {1}{5}×(7+5+7+a+7)=6$,解得$a=4.$
$s^{2}_{乙}=\frac {1}{5}×[(7-6)^{2}+(5-6)^{2}+(7-6)^{2}+(4-6)^{2}+(7-6)^{2}]=1.6$(环²).
(2) 因为两人成绩的平均水平(平均数)相同,根据方差可知,乙的成绩比甲稳定,所以乙将被选中.
(1) 因为两人各射了5箭,且总成绩相同,所以$\overline {x}_{乙}=\overline {x}_{甲}=6$环,即$\overline {x}_{乙}=\frac {1}{5}×(7+5+7+a+7)=6$,解得$a=4.$
$s^{2}_{乙}=\frac {1}{5}×[(7-6)^{2}+(5-6)^{2}+(7-6)^{2}+(4-6)^{2}+(7-6)^{2}]=1.6$(环²).
(2) 因为两人成绩的平均水平(平均数)相同,根据方差可知,乙的成绩比甲稳定,所以乙将被选中.
查看更多完整答案,请扫码查看


