《2025年小题狂做九年级数学上册苏科版巅峰版》

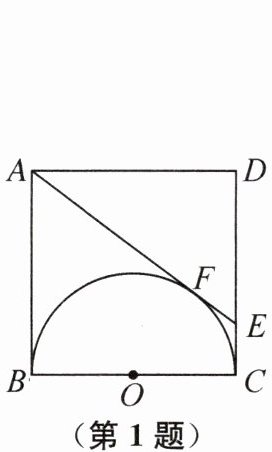
1. 如图,正方形 ABCD 的边长为 4 cm,以正方形的一边 BC 为直径在正方形 ABCD 的内部作半圆 O,过点 A 作半圆的切线,与半圆相切于点 F,与 DC 相交于点 E,则△ADE 的面积为(D)

$A.12 cm^2$
$B.24 cm^2$
$C.8 cm^2$
$D.6 cm^2$

答案： D

2. 如图,在矩形 ABCD 中,AD= 6,AB= 8,P 为边 BC 的中点,Q 是△ACD 的内切圆⊙O 上的一个动点,M 是 CQ 的中点,则 PM 长的最大值是(B)
A.$\sqrt{13}-1$
B.$\sqrt{13}+1$
C.3.2
D.$3\sqrt{2}$

答案： B 提示:因为四边形ABCD是矩形，所以∠D = 90°，CD = AB = 8。所以AC = $\sqrt{AD^{2}+CD^{2}}$ = 10。设△ADC的内切圆⊙O的半径为r，由等积法，可得$\frac{1}{2}$×10r + $\frac{1}{2}$×8r + $\frac{1}{2}$×6r = $\frac{1}{2}$×8×6(或由切线长定理，得6 - r + 8 - r = 10)，解得r = 2。连接OB，BQ。因为P是边BC的中点，M是CQ的中点，所以PM是△BCQ的中位线，所以PM = $\frac{1}{2}$BQ。当线段BQ经过圆心O时，BQ最长，此时PM最长。过点O分别作OE⊥AD于点E，OF⊥AB于点F，OG⊥CD于点G，则易得AF = OE = DE = OG = 2，所以BF = AB - AF = 6，OF = AE = AD - DE = 4。所以BO = $\sqrt{BF^{2}+OF^{2}}$ = 2$\sqrt{13}$。所以BQ长的最大值为BO + r = 2$\sqrt{13}$ + 2。所以PM长的最大值为$\sqrt{13}$ + 1。

3. 如图,⊙O 的直径 AB= 8,AM,BN 是它的两条切线,DE 与⊙O 相切于点 E,并与 AM,BN 分别相交于 D,C 两点,BD,OC 相交于点 F.若 CD= 10,则 BF 的长是(A)
A.$\frac{8\sqrt{17}}{9}$
B.$\frac{10\sqrt{17}}{9}$
C.$\frac{8\sqrt{15}}{9}$
D.$\frac{10\sqrt{15}}{9}$
]

答案： A 提示:以点O为坐标原点，水平向右为x轴正方向，以OA所在直线为y轴，竖直向上为y轴正方向构建平面直角坐标系xOy。过点D作DH⊥BC于点H，则可证四边形ABHD是矩形，所以AD = BH，DH = AB = 8，所以CH = $\sqrt{CD^{2}-DH^{2}}$ = 6。由切线长的性质可设BH = AD = DE = x，则EC = BC = BH + CH = x + 6。又因为DE + EC = CD，所以x + x + 6 = 10，解得x = 2。所以点D(2, 4)，C(8, -4)，B(0, -4)，所以直线OC的函数表达式为y = -$\frac{1}{2}$x，直线BD的函数表达式为y = 4x - 4。由$\begin{cases}y = -\frac{1}{2}x\\y = 4x - 4\end{cases}$，解得$\begin{cases}x = \frac{8}{9}\\y = -\frac{4}{9}\end{cases}$，所以点F($\frac{8}{9}$, -$\frac{4}{9}$)。所以BF = $\sqrt{(\frac{8}{9})^{2}+(-\frac{4}{9}+4)^{2}}$ = $\frac{8\sqrt{17}}{9}$。

4. 如图,已知 AB 是⊙O 的直径,CD,CB 是⊙O 的切线,D,B 为切点,OC 交⊙O 于点 E,AE 的延长线交 BC 于点 F,连接 AD,BD.现有以下四个结论:①AD//OC；②点 E 为△CDB 的内心；③FC= FE.其中正确的结论是(①②)
A.①②
B.②③
C.①③
D.①②③

答案： A 提示:连接OD，DE，BE。因为CD，BC是⊙O的切线，所以∠ODC = ∠OBC = 90°，OD = OB。易证Rt△CDO≌Rt△CBO(HL)，所以∠DOC = ∠BOC。可得∠BOC = $\frac{1}{2}$∠DOB = ∠DAB，所以AD//OC，故①正确。因为∠ODC = 90°，所以∠DOC + ∠DCO = 90° = ∠ODE + ∠CDE。因为OD = OE，所以∠ODE = ∠OED。所以2∠ODE + ∠DOC = 180°，所以∠CDE = $\frac{1}{2}$∠DOC。又因为∠BDE = $\frac{1}{2}$∠BOC，所以∠CDE = ∠BDE，即DE是∠CDB的平分线。同理可证得BE是∠CBD的平分线。所以点E为△CBD的内心，故②正确。若FC = FE，则∠OCB = ∠CEF = ∠OEA = ∠OAE，所以∠COB = ∠OAE + ∠OEA = 2∠OCB，所以∠COB = 60°，而∠COB不一定是60°，故③不正确。因此正确的结论是①②。

5. 已知四边形 ABCD 外切于⊙O,四边形 ABCD 的面积为 24,周长为 24,则⊙O 的半径为______2.

答案： 2

6. (泰州市兴化市期末)已知在 Rt△ABC 中,∠C= 90°,AC= 6,BC= 8,点 O 和点 M 分别为 Rt△ABC 的外心和内心,则线段 OM 的长为______$\sqrt{5}$.

答案： $\sqrt{5}$

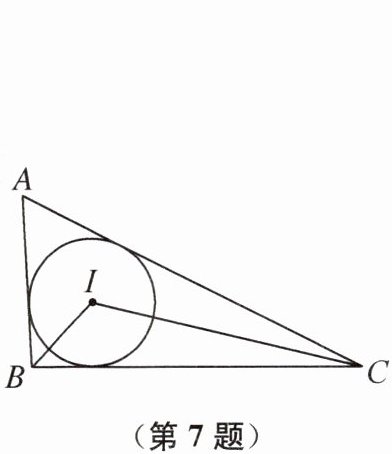
7. 如图,在△ABC 中,∠BAC= 60°,其周长为 24,⊙I 是△ABC 的内切圆,其半径为$\sqrt{3}$,则△ABC 的外接圆半径为______.
]

答案：
3$\sqrt{3}$ 提示:如图，设⊙I分别与△ABC的边相切于点D，E，F，连接AI，ID，IE，IF，则∠DAI = $\frac{1}{2}$∠BAC = 30°。所以AI = 2DI = 2$\sqrt{3}$，所以AF = AD = $\sqrt{AI^{2}-DI^{2}}$ = 3。因为BD = BE，CE = CF，所以BC = $\frac{1}{2}$×(24 - 2×3) = 9。设△ABC的外接圆圆心为O，连接OB，OC，过点O作OH⊥BC于点H，则∠BOC = 2∠BAC = 120°，易得∠BOH = $\frac{1}{2}$∠BOC = 60°，BH = $\frac{1}{2}$BC = $\frac{9}{2}$。设OH = x，则OB = 2x。在Rt△OBH中，由勾股定理，得$(\frac{9}{2})^{2}+x^{2}=(2x)^{2}$，解得x = $\frac{3\sqrt{3}}{2}$(负值已舍)。所以OB = 3$\sqrt{3}$，即△ABC的外接圆半径为3$\sqrt{3}$。

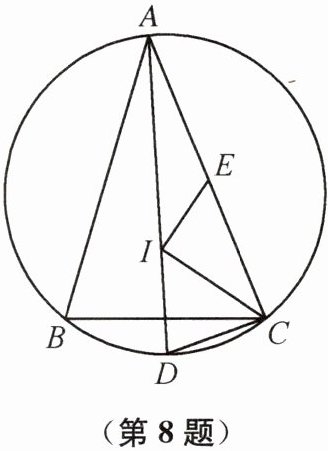
8. 如图,点 I 为△ABC 的内心,连接 AI 并延长交△ABC 的外接圆于点 D,AI= 2CD,E 为弦 AC 的中点,连接 EI,IC.若 IC= 6,ID= 5,则 IE 的长为______4.

答案： 4 提示:延长ID至点M，使DM = ID，连接CM。因为点I是△ABC的内心，所以∠IAC = ∠IAB = ∠BCD，∠ICA = ∠ICB。又因为∠DIC = ∠IAC + ∠ICA，∠DCI = ∠BCD + ∠ICB，所以∠DIC = ∠DCI，所以ID = DC = DM。易得∠ICM = 90°，IM = 2ID = 10。又因为IC = 6，所以CM = $\sqrt{IM^{2}-IC^{2}}$ = 8。因为AI = 2CD = 2ID = 10，所以AI = IM；又因为E为弦AC的中点，所以IE是△ACM的中位线，所以IE = $\frac{1}{2}$CM = 4。

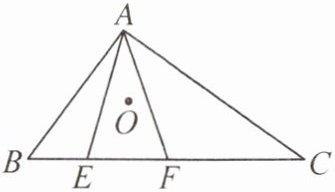
9. 如图,在△ABC 中,点 O 是内心,点 E,F 都在最长边 BC 上,已知 BF= BA,CE= CA.
(1)求证:点 O 是△AEF 的外心.
(2)若∠B= 40°,∠C= 30°,求∠EOF 的度数.
]

答案：
(1)证明:连接OA，OB，OC，OE，OF。因为点O是△ABC的内心，所以∠OBA = ∠OBF。易证△ABO≌△FBO，所以OA = OF。同理可证OA = OE。所以OA = OE = OF，所以点O是△AEF的外心。
(2)解:连接OE，OF。因为点O是△AEF的外心，所以∠EOF = 2∠EAF。在等腰三角形BAF中，∠AFE = 90° - $\frac{1}{2}$∠B = 70°。同理可得∠AEF = 90° - $\frac{1}{2}$∠C = 75°。所以∠EOF = 2∠EAF = 2(180° - ∠AEF - ∠AFE) = 70°。