9. 如图,已知$\triangle ABC内接于\odot O$,$\angle BAC= 60^{\circ}$,D是BC的中点,且$\angle AOD= 166^{\circ}$,AE,CF分别是边BC,AB上的高,则$\angle BCF$的度数为______
$23^{\circ}$
.
答案:
$23^{\circ}$ 提示:连接BO,CO.因为$\angle BAC = 60^{\circ}$,所以$\angle BOC = 2\angle BAC = 120^{\circ}$.因为$OB = OC$,D是BC的中点,所以$\angle BOD=\frac{1}{2}\angle BOC = 60^{\circ}$,$OD\perp BC$.又由$\angle AOD = 166^{\circ}$,可得$\angle AOB=\angle AOD - \angle BOD = 106^{\circ}$,所以$\angle BAO=\frac{1}{2}×(180^{\circ}-\angle AOB)=37^{\circ}$.因为AE,CF分别是边BC,AB上的高,所以$AE\perp BC$,$CF\perp AB$.又因为$OD\perp BC$,所以$AE// OD$,所以$\angle OAE = 180^{\circ}-\angle AOD = 14^{\circ}$.所以$\angle BAE=\angle BAO - \angle OAE = 23^{\circ}$.易知$\angle BCF+\angle ABC = 90^{\circ}=\angle BAE+\angle ABC$,所以$\angle BCF=\angle BAE = 23^{\circ}$.
10. 如图,已知$\angle AOB= 45^{\circ}$,在边OA,OB上分别有两个动点C,D,连接CD,以CD为直角边作等腰直角三角形CDE.当CD的长度保持不变且等于2cm时,OE长的最大值是______.


答案:
$(\sqrt{2}+\sqrt{10})$cm 提示:如图,在CD的左侧,以CD为斜边,作等腰直角三角形CDF,以点F为圆心,CF为半径作$\odot F$.将C,D,E看作定点,O为动点.因为$\angle AOB = 45^{\circ}=\frac{1}{2}\angle CFD$,所以点O在优弧$\widehat{CD}$上运动,则当O,F,E三点共线时,OE的值最大.因为$\triangle CDF$和$\triangle CDE$均是等腰直角三角形,所以$\angle CDF=\angle CDE = 45^{\circ}$,所以$\angle EDF = 90^{\circ}$.又因为$CD = 2$cm,所以$DE = 2\sqrt{2}$cm,$DF = \sqrt{2}$cm.由勾股定理,得$EF=\sqrt{DF^{2}+DE^{2}}=\sqrt{10}$cm.所以$OE = OF + EF = (\sqrt{2}+\sqrt{10})$cm,即OE长的最大值是$(\sqrt{2}+\sqrt{10})$cm.

$(\sqrt{2}+\sqrt{10})$cm 提示:如图,在CD的左侧,以CD为斜边,作等腰直角三角形CDF,以点F为圆心,CF为半径作$\odot F$.将C,D,E看作定点,O为动点.因为$\angle AOB = 45^{\circ}=\frac{1}{2}\angle CFD$,所以点O在优弧$\widehat{CD}$上运动,则当O,F,E三点共线时,OE的值最大.因为$\triangle CDF$和$\triangle CDE$均是等腰直角三角形,所以$\angle CDF=\angle CDE = 45^{\circ}$,所以$\angle EDF = 90^{\circ}$.又因为$CD = 2$cm,所以$DE = 2\sqrt{2}$cm,$DF = \sqrt{2}$cm.由勾股定理,得$EF=\sqrt{DF^{2}+DE^{2}}=\sqrt{10}$cm.所以$OE = OF + EF = (\sqrt{2}+\sqrt{10})$cm,即OE长的最大值是$(\sqrt{2}+\sqrt{10})$cm.

11. 方程$(x^{2}+3x-4)^{2}+(2x^{2}-7x+6)^{2}= (3x^{2}-4x+2)^{2}$的负整数解为
$-4$
.
答案:
$x = -4$ 提示:设$x^{2}+3x - 4 = a$,$2x^{2}-7x + 6 = b$,则$3x^{2}-4x + 2 = a + b$.可得$a^{2}+b^{2}=(a + b)^{2}$,所以$ab = 0$,所以$x^{2}+3x - 4 = 0$或$2x^{2}-7x + 6 = 0$,解得$x_{1}=-4$,$x_{2}=1$或$x_{3}=\frac{3}{2}$,$x_{4}=2$,故负整数解为$x = -4$.
12. 某农户在山上种脐橙果树44株,现进入第三年收获.收获时,先随机采摘5株果树上的脐橙,称得每株果树上脐橙的质量如下(单位:kg):35,35,34,39,37.
(1)试估计这一年该农户脐橙的总产量.
(2)若市场上每千克脐橙售价5元,求该农户这一年卖脐橙的收入.
(3)已知该农户第一年的果树收入为5500元,根据以上数据,估算第二年、第三年卖脐橙收入的年平均增长率.
(1)试估计这一年该农户脐橙的总产量.
(2)若市场上每千克脐橙售价5元,求该农户这一年卖脐橙的收入.
(3)已知该农户第一年的果树收入为5500元,根据以上数据,估算第二年、第三年卖脐橙收入的年平均增长率.
答案:
(1)样本平均数为$(35 + 35 + 34 + 39 + 37)÷5 = 36$(kg),所以这一年该农户脐橙的总产量约为$36×44 = 1584$(kg).
(2)该农户这一年卖脐橙的收入为$5×1584 = 7920$(元).
(3)设年平均增长率为x.根据题意,得$5500(1 + x)^{2}=7920$,解得$x_{1}=0.2 = 20\%$,$x_{2}=-2.2$(不合题意,舍去).答:第二年、第三年卖脐橙收入的年平均增长率约为20%.
(1)样本平均数为$(35 + 35 + 34 + 39 + 37)÷5 = 36$(kg),所以这一年该农户脐橙的总产量约为$36×44 = 1584$(kg).
(2)该农户这一年卖脐橙的收入为$5×1584 = 7920$(元).
(3)设年平均增长率为x.根据题意,得$5500(1 + x)^{2}=7920$,解得$x_{1}=0.2 = 20\%$,$x_{2}=-2.2$(不合题意,舍去).答:第二年、第三年卖脐橙收入的年平均增长率约为20%.
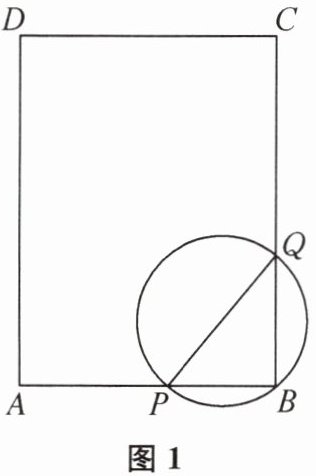
13. 如图1,在矩形ABCD中,$AB= 6cm$,$BC= 8cm$,点P以3cm/s的速度从点A向点B运动,点Q以4cm/s的速度从点C向点B运动.点P,Q同时出发,运动时间为t s($0<t<2$),$\odot M是\triangle PQB$的外接圆.
(1)当$t= 1$时,$\odot M$的半径是______cm,$\odot M$与直线CD的位置关系是______.
(2)在点P从点A向点B运动的过程中,
①圆心M运动的路径长是______cm;
②当$\odot M$与直线CD相切时,求t的值.
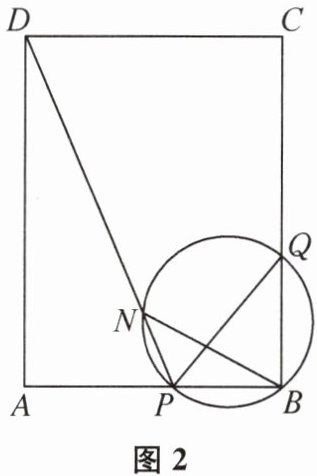
(3)如图2,连接PD,交$\odot M$于点N,当$\angle APD= \angle NBQ$时,求t的值.
[答案]:(1)
(2)①
②当$\odot M$与CD相切时,设切点为E,连接EM并延长交AB于点F,则$EF\perp AB$,$EF\perp CD$.由条件可知,$BQ=(8 - 4t)$cm,$PB=(6 - 3t)$cm,所以由勾股定理,得$PQ=\sqrt{BQ^{2}+PB^{2}}=(10 - 5t)$cm,所以$PM = EM=(5-\frac{5}{2}t)$cm.易知MF是$\triangle BPQ$的中位线,所以$MF=\frac{1}{2}BQ=(4 - 2t)$cm.因为$EF = BC = EM + MF$,所以$5-\frac{5}{2}t + 4 - 2t = 8$,解得$t=\frac{2}{9}$.
(3)过点D作$DG\perp PQ$于点G,连接DQ.因为$\angle APD=\angle NBQ$,$\angle NBQ=\angle NPQ$,所以$\angle APD=\angle NPQ$.易证$Rt\triangle APD\cong Rt\triangle GPD$,所以$PG = PA = 3t$cm,$DG = DA = 8$cm.由
(2)②知,$PQ=(10 - 5t)$cm,所以$QG=|3t-(10 - 5t)|=|8t - 10|$cm.由勾股定理,得$DC^{2}+CQ^{2}=DQ^{2}=DG^{2}+QG^{2}$,即$6^{2}+(4t)^{2}=8^{2}+(8t - 10)^{2}$.整理,得$3t^{2}-10t + 8 = 0$,即$(t - 2)(3t - 4)=0$,解得$t_{1}=2$(不合题意,舍去),$t_{2}=\frac{4}{3}$.所以t的值为
(1)当$t= 1$时,$\odot M$的半径是______cm,$\odot M$与直线CD的位置关系是______.
(2)在点P从点A向点B运动的过程中,
①圆心M运动的路径长是______cm;
②当$\odot M$与直线CD相切时,求t的值.
(3)如图2,连接PD,交$\odot M$于点N,当$\angle APD= \angle NBQ$时,求t的值.


[答案]:(1)
$\frac{5}{2}$
相离
(2)①
5
②当$\odot M$与CD相切时,设切点为E,连接EM并延长交AB于点F,则$EF\perp AB$,$EF\perp CD$.由条件可知,$BQ=(8 - 4t)$cm,$PB=(6 - 3t)$cm,所以由勾股定理,得$PQ=\sqrt{BQ^{2}+PB^{2}}=(10 - 5t)$cm,所以$PM = EM=(5-\frac{5}{2}t)$cm.易知MF是$\triangle BPQ$的中位线,所以$MF=\frac{1}{2}BQ=(4 - 2t)$cm.因为$EF = BC = EM + MF$,所以$5-\frac{5}{2}t + 4 - 2t = 8$,解得$t=\frac{2}{9}$.
(3)过点D作$DG\perp PQ$于点G,连接DQ.因为$\angle APD=\angle NBQ$,$\angle NBQ=\angle NPQ$,所以$\angle APD=\angle NPQ$.易证$Rt\triangle APD\cong Rt\triangle GPD$,所以$PG = PA = 3t$cm,$DG = DA = 8$cm.由
(2)②知,$PQ=(10 - 5t)$cm,所以$QG=|3t-(10 - 5t)|=|8t - 10|$cm.由勾股定理,得$DC^{2}+CQ^{2}=DQ^{2}=DG^{2}+QG^{2}$,即$6^{2}+(4t)^{2}=8^{2}+(8t - 10)^{2}$.整理,得$3t^{2}-10t + 8 = 0$,即$(t - 2)(3t - 4)=0$,解得$t_{1}=2$(不合题意,舍去),$t_{2}=\frac{4}{3}$.所以t的值为
$\frac{4}{3}$
.
答案:
(1)$\frac{5}{2}$ 相离
(2)①5 提示:易知PQ的中点是圆心M所在位置.连接AC,BD,相交于点O.由点P,Q运动速度之比与AB,BC长度之比相等可知,圆心M在对角线BD上.结合题图,由运动的初末位置可知,点M运动的路径长是$OB=\frac{1}{2}BD = 5$cm.
②当$\odot M$与CD相切时,设切点为E,连接EM并延长交AB于点F,则$EF\perp AB$,$EF\perp CD$.由条件可知,$BQ=(8 - 4t)$cm,$PB=(6 - 3t)$cm,所以由勾股定理,得$PQ=\sqrt{BQ^{2}+PB^{2}}=(10 - 5t)$cm,所以$PM = EM=(5-\frac{5}{2}t)$cm.易知MF是$\triangle BPQ$的中位线,所以$MF=\frac{1}{2}BQ=(4 - 2t)$cm.因为$EF = BC = EM + MF$,所以$5-\frac{5}{2}t + 4 - 2t = 8$,解得$t=\frac{2}{9}$.
(3)过点D作$DG\perp PQ$于点G,连接DQ.因为$\angle APD=\angle NBQ$,$\angle NBQ=\angle NPQ$,所以$\angle APD=\angle NPQ$.易证$Rt\triangle APD\cong Rt\triangle GPD$,所以$PG = PA = 3t$cm,$DG = DA = 8$cm.由
(2)②知,$PQ=(10 - 5t)$cm,所以$QG=|3t-(10 - 5t)|=|8t - 10|$cm.由勾股定理,得$DC^{2}+CQ^{2}=DQ^{2}=DG^{2}+QG^{2}$,即$6^{2}+(4t)^{2}=8^{2}+(8t - 10)^{2}$.整理,得$3t^{2}-10t + 8 = 0$,即$(t - 2)(3t - 4)=0$,解得$t_{1}=2$(不合题意,舍去),$t_{2}=\frac{4}{3}$.所以t的值为$\frac{4}{3}$.
(1)$\frac{5}{2}$ 相离
(2)①5 提示:易知PQ的中点是圆心M所在位置.连接AC,BD,相交于点O.由点P,Q运动速度之比与AB,BC长度之比相等可知,圆心M在对角线BD上.结合题图,由运动的初末位置可知,点M运动的路径长是$OB=\frac{1}{2}BD = 5$cm.
②当$\odot M$与CD相切时,设切点为E,连接EM并延长交AB于点F,则$EF\perp AB$,$EF\perp CD$.由条件可知,$BQ=(8 - 4t)$cm,$PB=(6 - 3t)$cm,所以由勾股定理,得$PQ=\sqrt{BQ^{2}+PB^{2}}=(10 - 5t)$cm,所以$PM = EM=(5-\frac{5}{2}t)$cm.易知MF是$\triangle BPQ$的中位线,所以$MF=\frac{1}{2}BQ=(4 - 2t)$cm.因为$EF = BC = EM + MF$,所以$5-\frac{5}{2}t + 4 - 2t = 8$,解得$t=\frac{2}{9}$.
(3)过点D作$DG\perp PQ$于点G,连接DQ.因为$\angle APD=\angle NBQ$,$\angle NBQ=\angle NPQ$,所以$\angle APD=\angle NPQ$.易证$Rt\triangle APD\cong Rt\triangle GPD$,所以$PG = PA = 3t$cm,$DG = DA = 8$cm.由
(2)②知,$PQ=(10 - 5t)$cm,所以$QG=|3t-(10 - 5t)|=|8t - 10|$cm.由勾股定理,得$DC^{2}+CQ^{2}=DQ^{2}=DG^{2}+QG^{2}$,即$6^{2}+(4t)^{2}=8^{2}+(8t - 10)^{2}$.整理,得$3t^{2}-10t + 8 = 0$,即$(t - 2)(3t - 4)=0$,解得$t_{1}=2$(不合题意,舍去),$t_{2}=\frac{4}{3}$.所以t的值为$\frac{4}{3}$.
查看更多完整答案,请扫码查看


