1. 某次器乐比赛设置了6个获奖名额,共有11名选手参加,他们的比赛得分均不相同. 若知道某位选手的得分,要判断他能否获奖,在下列11名选手成绩的统计量中,只需知道 (
A.方差
B.平均数
C.众数
D.中位数
D
)A.方差
B.平均数
C.众数
D.中位数
答案:
D
2. 已知圆锥侧面展开图的圆心角为90°,则该圆锥的底面半径与母线长的比为 (
A.1:2
B.2:1
C.1:4
D.4:1
C
)A.1:2
B.2:1
C.1:4
D.4:1
答案:
C
3. (无锡市宜兴市期中)在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴的距离等于1,则该圆的半径r的取值范围是 (
A.r>4
B.0<r<6
C.4≤r<6
D.4<r<6
D
)A.r>4
B.0<r<6
C.4≤r<6
D.4<r<6
答案:
D
4. (苏州市常熟市模拟)已知反比例函数$y= \frac{ab}{x}$,当x>0时,y随x的增大而增大,则关于x的方程$ax^{2}-2x+b= 0$的根的情况是 (
A.有两个正实数根
B.有两个负实数根
C.有一个正实数根和一个负实数根
D.没有实数根
C
)A.有两个正实数根
B.有两个负实数根
C.有一个正实数根和一个负实数根
D.没有实数根
答案:
C 提示:由题意,得ab<0.所以(-2)² - 4ab = 4 - 4ab > 0,且a≠0,所以方程有两个不相等的实数根.由根与系数的关系,得$x_{1}x_{2}=\frac{b}{a}<0$,所以方程有一个正实数根和一个负实数根.
5. 若实数m满足$(m^{2}-m+1)^{2}= 4$,则$m^{2}-m$的值为 (
A.1或-3
B.1
C.-3
D.0
B
)A.1或-3
B.1
C.-3
D.0
答案:
B 提示:设$m^{2}-m=t$,原方程化为$(t + 1)^{2}=4$,解得$t_{1}=1,t_{2}=-3$.又因为$t=m^{2}-m=(m - \frac{1}{2})^{2}-\frac{1}{4}\geq-\frac{1}{4}$,所以$t_{2}=-3$应舍去.所以$m^{2}-m=1$.
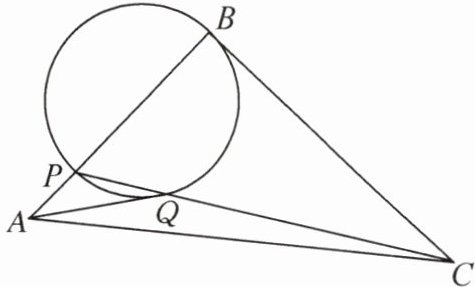
6. 如图,在$\triangle ABC$中,$\angle ABC= 90^{\circ}$,AB= 6,P是边AB上的一个动点,以BP为直径的圆交CP于点Q. 若线段AQ长的最小值是3,则$\triangle ABC$的面积为 ( )
A.18
B.27
C.36
D.54

A.18
B.27
C.36
D.54
答案:
B 提示:如图,取BC的中点T,连接BQ,AT,QT.因为PB是⊙O的直径,所以∠PQB = 90°.所以∠CQB = 90°.所以$QT=\frac{1}{2}BC = BT$.易知QT,AT均为定值,且AQ≥AT - QT,所以当点A,Q,T共线时,AQ的值最小.此时设$BT = QT = x$,则AT = 3 + x.在Rt△ABT中,由勾股定理,得$AT^{2}=BT^{2}+AB^{2}$,即$(3 + x)^{2}=x^{2}+6^{2}$,解得$x=\frac{9}{2}$.所以$BT=\frac{9}{2}$,所以BC = 2BT = 9.所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC = 27$.
B 提示:如图,取BC的中点T,连接BQ,AT,QT.因为PB是⊙O的直径,所以∠PQB = 90°.所以∠CQB = 90°.所以$QT=\frac{1}{2}BC = BT$.易知QT,AT均为定值,且AQ≥AT - QT,所以当点A,Q,T共线时,AQ的值最小.此时设$BT = QT = x$,则AT = 3 + x.在Rt△ABT中,由勾股定理,得$AT^{2}=BT^{2}+AB^{2}$,即$(3 + x)^{2}=x^{2}+6^{2}$,解得$x=\frac{9}{2}$.所以$BT=\frac{9}{2}$,所以BC = 2BT = 9.所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC = 27$.

7. 为估计某地区黄羊的数量,先捕捉20只黄羊,并分别给它们做上标记,然后放回,待有标志的黄羊完全混合于黄羊群后,第二次捕捉40只黄羊,发现其中两只有标记,从而估计该地区有黄羊
400
只.
答案:
400
8. (盐城市期末)若$\odot O是\triangle ABC$的外接圆,且$\angle OAB= 50^{\circ}$,则$\angle ACB$的度数为
40°或140°
.
答案:
40°或140°
9. 若方程$x^{2}-2x+\frac{\sqrt{3}}{2}= 0$的两个根$\alpha,\beta$也是关于x的方程$x^{4}+px^{2}+q= 0$的两个根,则p=
$\sqrt{3}-4$
.
答案:
$\sqrt{3}-4$
10. 从$-4,-\frac{7}{2},0,\frac{7}{2},4$这五个数中,任取一个数作为a的值,恰好使得关于x的一元二次方程$2ax^{2}-6x-1= 0$有两个不相等的实数根,且使两个根都在-1和1之间(包括-1和1),则取到满足条件的a值的概率为
$\frac{4}{5}$
.
答案:
$\frac{4}{5}$
11. 如图,在Rt$\triangle ABC$中,$\angle ACB= 90^{\circ}$,AC= 16,BC= 12,点P在以AB为直径的半圆上运动,由点B运动到点A,连接CP,M是CP的中点,则点M经过的路径长为
5π
.
答案:
5π 提示:因为∠ACB = 90°,AC = 16,BC = 12,所以$AB=\sqrt{AC^{2}+BC^{2}}=20$.连接AP,BP,则∠APB = 90°.取BC,AC的中点E,F,连接ME,MF,EF.易证$ME// BP,ME=\frac{1}{2}BP$;$MF// AP,MF=\frac{1}{2}AP$.所以∠EMF = 90°,且$EF=\frac{1}{2}AB = 10$.由点P的运动过程可知,点M在以EF为直径的半圆上运动,所以点M经过的路径长为$\frac{1}{2}×2\pi×5 = 5\pi$.
查看更多完整答案,请扫码查看


