1. 用相同的正方形砖块铺成的地板如图所示,一宝物藏在某一砖块下面,则宝物在白色区域的概率是(
A.$\frac{1}{6}$
B.$\frac{2}{9}$
C.$\frac{1}{2}$
D.$\frac{5}{9}$
D
)A.$\frac{1}{6}$
B.$\frac{2}{9}$
C.$\frac{1}{2}$
D.$\frac{5}{9}$
答案:
D
2. 在盒子里放有三张分别写有整式$a^{2}+2a+1$,$a-1$,$a^{2}-1(a≠±1)$的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成最简分式的概率是(
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{6}$
D.$\frac{3}{4}$
A
)A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{6}$
D.$\frac{3}{4}$
答案:
A
3. 如图,小球从A口往下落,在每个交叉口都有向左和向右两种可能,且可能性相同,则小球最终从E口落出的概率为(
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
D.$\frac{1}{8}$
B
)A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
D.$\frac{1}{8}$
答案:
B
4. 有9张卡片,它们的形状、大小以及背面的颜色均相同,其正面分别写有1~9这九个数字. 将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则使关于x的不等式组$\left\{\begin{array}{l} 4x\geq 3(x+1),\\ 2x-\frac{x-1}{2}<a\end{array} \right. $有解的概率为(
A.$\frac{2}{9}$
B.$\frac{1}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$
C
)A.$\frac{2}{9}$
B.$\frac{1}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$
答案:
C 提示:解不等式组,得$3\leqslant x<\frac{2a-1}{3}$.因为原不等式组有解,所以$\frac{2a-1}{3}>3$,解得$a>5$.所以a的可能值为6,7,8,9,共4种可能性.所以所求概率为$\frac{4}{9}$.
5. 如图是古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC. $\triangle ABC$的三边所围成的阴影区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ. 在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为$P_{1}$,$P_{2}$,$P_{3}$,则(
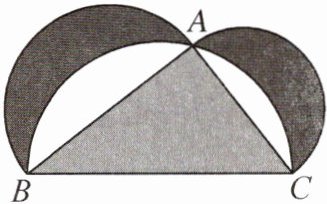
A.$P_{1}= P_{2}$
B.$P_{1}= P_{3}$
C.$P_{2}= P_{3}$
D.$P_{1}= P_{2}+P_{3}$
A
)
A.$P_{1}= P_{2}$
B.$P_{1}= P_{3}$
C.$P_{2}= P_{3}$
D.$P_{1}= P_{2}+P_{3}$
答案:
A 提示:设$BC=2r_{1},AB=2r_{2},AC=2r_{3}$,则$r_{1}^{2}=r_{2}^{2}+r_{3}^{2}$.易知$S_{1}=\frac{1}{2}×4r_{2}r_{3}=2r_{2}r_{3}$,$S_{Ⅲ}=\frac{1}{2}\pi r_{1}^{2}-2r_{2}r_{3}$,$S_{Ⅱ}=\frac{1}{2}\pi r_{3}^{2}+\frac{1}{2}\pi r_{2}^{2}-S_{Ⅲ}=\frac{1}{2}\pi r_{3}^{2}+\frac{1}{2}\pi r_{2}^{2}-\frac{1}{2}\pi r_{1}^{2}+2r_{2}r_{3}=2r_{2}r_{3}$,所以$S_{1}=S_{Ⅱ}$,即$P_{1}=P_{2}$.
6. 某医院准备从报名的甲、乙、丙、丁四名医生中随机选择两人去支援社区医院,那么乙、丙两人中至少有一人被选中的概率为
$\frac{5}{6}$
.
答案:
$\frac{5}{6}$
7. (泰州市泰兴市模拟)一个盒子中装有大小、形状一模一样的x颗白色弹珠和y颗黑色弹珠,从盒中随机取出一颗弹珠,取得白色弹珠的概率是$\frac{1}{3}$. 若再往盒中放进12颗同样的白色弹珠,取得白色弹珠的概率是$\frac{2}{3}$,则原来盒中有白色弹珠
4
颗.
答案:
4
8. 一枚质地均匀的正方体骰子六个面上分别标有$-3$,$-\frac{1}{2}$,0,1,2,4这六个数. 若将第一次掷出骰子正面朝上的数记为a,第二次掷出骰子正面朝上的数记为b,则点$(a,b)恰好落在一次函数y= x-4$的图像与坐标轴所围成的三角形区域内(含边界)的概率为
$\frac{1}{4}$
.
答案:
$\frac{1}{4}$
9. 如图,管中放置着三根同样的绳子$AA_{1}$,$BB_{1}$,$CC_{1}$. 小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连接成一根长绳的概率为
$\frac{2}{3}$
.
答案:
$\frac{2}{3}$
查看更多完整答案,请扫码查看


