《2025年小题狂做九年级数学上册苏科版巅峰版》

1. 在平面直角坐标系 xOy 中,以原点 O 为圆心,4 为半径作圆,则该圆上到直线 $ y= -x+\sqrt{2} $ 的距离等于 2 的点共有 (D)
A.1个
B.2个
C.3个
D.4个

答案： D

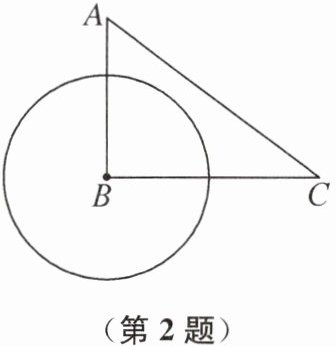
2. 题目：“如图,在 $ \text{Rt}\triangle ABC $ 中,$ \angle B= 90^\circ $,$ AB= 3 $,$ AC= 5 $,以点 B 为圆心的 $ \odot B $ 的半径为 r. 若对于 r 的一个值,$ \odot B $ 与边 AC 只有一个公共点,求 r 的取值范围.” 对于其答案,甲答：$ r= 4 $. 乙答：$ 3＜r＜4 $. 丙答：$ r= \frac{12}{5} $. 则正确的是 (D)

A.只有乙答的对
B.甲、乙的答案合在一起才完整
C.乙、丙的答案合在一起才完整
D.三人的答案合在一起才完整

答案： D

3. 如图,在梯形 ABCD 中,$ AD// BC $,$ \angle B= 90^\circ $,$ AD= 2 $,$ AB= 4 $,$ BC= 6 $,O 是边 BC 上一点. 若以点 O 为圆心,OC 为半径的 $ \odot O $ 与边 AD 只有一个公共点,则 OC 长的取值范围是 (B)
A.$ 4＜OC\leqslant \frac{13}{3} $
B.$ 4\leqslant OC\leqslant \frac{13}{3} $
C.$ 4＜OC\leqslant \frac{14}{3} $
D.$ 4\leqslant OC\leqslant \frac{14}{3} $

答案： B 提示:过点D作DE⊥BC于点E,则DE=AB=4,BE=AD=2,所以CE=4=DE.当⊙O与边AD相切，切点为D时，圆心O与点E重合,即OC=4;当OA=OC时,⊙O与AD交于点A,设OA=OC=x,则OB=6−x,在Rt△ABO中,由勾股定理，得4²+(6−x)²=x²,解得x=$\frac{13}{3}$,所以⊙O与边AD只有一个公共点时，OC长的取值范围是4≤OC≤$\frac{13}{3}$.

4. 如图,在平面直角坐标系 xOy 中,点 A 在第二象限,$ \odot A $ 与 x 轴、y 轴都相切. 若将 $ \odot A $ 向右平移 5 个单位长度,圆心 A 恰好落在直线 $ y= 2x-4 $ 上,则 $ \odot A $ 的半径为2.

答案： 2

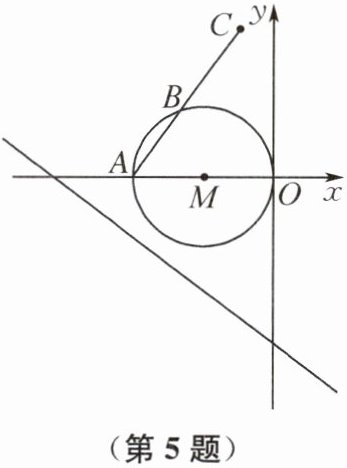
5. 如图,点 A 的坐标是 $ (a,0)(a＜0) $,B 是以 OA 为直径的 $ \odot M $ 上一动点,点 A 关于点 B 的对称点为 C. 当点 B 在 $ \odot M $ 上运动时,所有这样的点 C 组成的图形与直线 $ y= -\frac{3}{4}x-3 $ 有且只有一个公共点,则 a 的值等于______.

答案：
−$\frac{12}{5}$ 提示:如图，连接BM,OC，设直线y=−$\frac{3}{4}$x−3交x轴于点E,交y轴于点F.易得OE=4,OF=3,所以EF=$\sqrt{OE²+OF²}$=5.因为AB=BC,AM=OM,点A(a,0),所以OC=2BM=−a.所以点C的运动轨迹是以点O为圆心,−a为半径的圆.当⊙O与直线y=−$\frac{3}{4}$x−3相切时,⊙O与直线y=−$\frac{3}{4}$x−3有且只有一个公共点.设切点为G,连接OG.在Rt△EOF中,易知OG⊥EF，由等积法，得$\frac{1}{2}$OE·OF=$\frac{1}{2}$EF·OG,所以OG=$\frac{12}{5}$.所以a=−$\frac{12}{5}$.

6. 在 $ \triangle ABC $ 中,$ AB= AC= 4 $,$ \angle A= 120^\circ $,D 是 AB 的中点,以点 D 为圆心作 $ \odot D $,若 $ \odot D $ 与边 BC 只有一个公共点,则 $ \odot D $ 的半径 r 应满足______r=1或2＜r≤2$\sqrt{7}$.

答案： r=1或2＜r≤2$\sqrt{7}$ 提示:过点D作DE⊥BC于点E,过点A作AF⊥BC于点F,连接CD.因为AB=AC=4,∠BAC=120°,D是AB的中点,所以∠B=∠C=30°,BD=2.所以DE=1,BE=$\sqrt{3}$,AF=2,BF=2$\sqrt{3}$.所以BC=2BF=4$\sqrt{3}$,所以EC=BC−BE=3$\sqrt{3}$,CD=$\sqrt{DE²+EC²}$=2$\sqrt{7}$.当DE=r,即r=1时,⊙D与边BC只有一个公共点;当点B在圆内部，点C在⊙D上或在⊙D外时,即2＜r≤2$\sqrt{7}$时，⊙D与边BC同样只有一个公共点.

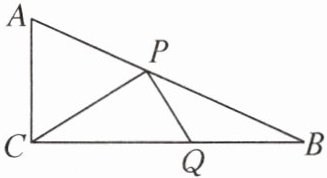
7. 如图,在 $ \text{Rt}\triangle ABC $ 中,$ AC= 5 $,$ BC= 12 $,$ \angle ACB= 90^\circ $,P 是边 AB 上的动点,Q 是边 BC 上的动点,且 $ \angle CPQ= 90^\circ $,则线段 CQ 长的取值范围是______$\frac{20}{3}$≤CQ≤12.

答案： $\frac{20}{3}$≤CQ≤12 提示:在Rt△ABC中，AC=5,BC=12,∠ACB=90°,所以AB=13.以CQ为直径作半圆O.①当半圆O与AB相切时，连接OP，则OP⊥AB,且AP=AC=5,所以PB=AB−AP=8.设CO=x,则OP=x,OB=12−x.在Rt△OPB中,OB²=OP²+PB²,即(12−x)²=x²+8²,解得x=$\frac{10}{3}$,所以CQ=2x=$\frac{20}{3}$,故当CQ=$\frac{20}{3}$且点P运动到切点的位置时,∠CPQ=90°.②当$\frac{20}{3}$＜CQ＜12时,半圆O与直线AB有两个交点，当点P运动到这两个交点的位置时,∠CPQ=90°.③当CQ=12时,点Q与点B重合,此时半圆O与AB(除点B外)仅有一个交点，当点P运动到这个交点时,∠CPQ=90°.④当0＜CQ＜$\frac{20}{3}$时，半圆O与直线AB相离，即当点P在边AB上运动时，均在半圆O外，∠CPQ＜90°,不合题意，舍去.综上所述，线段CQ长的取值范围是$\frac{20}{3}$≤CQ≤12.

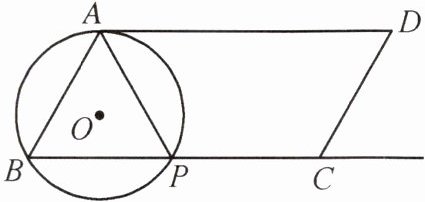
8. 如图,在 $ □ ABCD $ 中,$ AB= 4 $,$ BC= 8 $,$ \angle ABC= 60^\circ $,P 是射线 BC 上一动点,作 $ \triangle PAB $ 的外接圆 $ \odot O $.
(1)当直线 DC 与 $ \triangle PAB $ 的外接圆 $ \odot O $ 相切时,求 $ \odot O $ 的半径.
(2)直接写出 $ \odot O $ 与 $ □ ABCD $ 的边的公共点个数及对应 BP 长的取值范围.

答案：
解:
(1)如图1,取AB的中点G,作GF⊥AB,交DC的延长线于点F,交BC于点E,则点O在线段FG上,BG=$\frac{1}{2}$AB=2,GF⊥CD.所以F为直线DC与⊙O的切点,又因为∠ABC=60°,所以∠BEG=30°.所以BE=2BG=4.所以EG=$\sqrt{BE²−BG²}$=2$\sqrt{3}$,EC=BC−BE=4=BE.可证△BEG≌△CEF.所以EF=EG=2$\sqrt{3}$.所以FG=EF+EG=4$\sqrt{3}$.连接OB，设⊙O的半径为r,则OB=OF=r.在Rt△OBG中,OG=$\sqrt{OB²−BG²}$=$\sqrt{r²−4}$.因为OG+OF=FG,所以$\sqrt{r²−4}$+r=4$\sqrt{3}$,解得r=$\frac{13\sqrt{3}}{6}$,经检验，符合要求.所以⊙O的半径为$\frac{13\sqrt{3}}{6}$.

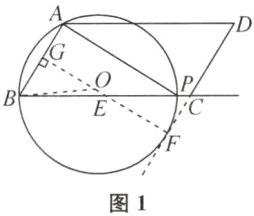
(2)当⊙O与▱ABCD的边的公共点个数为2时，BP＞12;当⊙O与▱ABCD的边的公共点个数为3时,0＜BP≤4或BP=12;当⊙O与▱ABCD的边的公共点个数为4时，4＜BP＜12. 提示:当AD与⊙O相切时，如图2,此时切点必为A.连接AO并延长，交BC于点H,则∠DAH=∠AHB=90°.连接OB,OP,则BH=HP.所以AP=AB.又因为∠ABC=60°,所以△ABP是等边三角形,所以BP=AB=4.易知当0＜BP≤4时,⊙O与▱ABCD的边有3个公共点.当⊙O经过点D时，如图3,连接BD,DP.易知AD//BC,所以∠ADB=∠DBP，可得AB=DP.又因为AB=CD,所以CD=DP.易知∠DCP=∠ABC=60°.所以△CDP是等边三角形，所以CP=CD=AB=4,所以BP=BC+CP=12.易知当4＜BP＜12时，⊙O与▱ABCD的边有4个公共点;当BP=12时，⊙O与▱ABCD的边有3个公共点;当BP＞12时，点D在⊙O的内部，⊙O与▱ABCD的边有2个公共点.