《2025年小题狂做九年级数学上册苏科版巅峰版》

1. 已知 m,n,s,t 为互不相等的实数,且(m+s)(m+t)= 2,(n+s)(n+t)= 2,则mn-st的值为(A)
A.-2
B.0
C.$\frac{1}{2}$
D.2

答案： A 提示:因为(m+s)(m+t)=2,(n+s)(n+t)=2,所以m²+m(s+t)+st-2=0,n²+n(s+t)+st-2=0.因为m,n,s,t为互不相等的实数，所以m和n可以看作关于x的一元二次方程x²+x(s+t)+st-2=0的两个根.由根与系数的关系，可得mn=st-2.所以mn-st=-2.

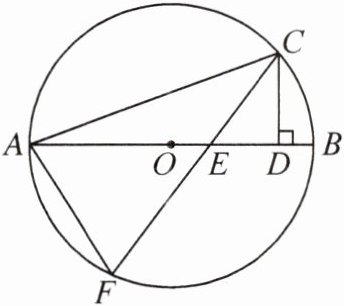
2. 如图,AB 是$\odot O$的直径,点 C 在$\odot O$上,CD⊥AB,垂足为 D,∠ACD 的平分线交AB 于点 E,交$\odot O$于点 F. 若$\odot O$的直径为 6,BE= 2,则 AF 的长为______2√3.

答案： 2√3 提示:连接BC,BF,OF,延长CD交⊙O于点H,过点F作FN⊥AB于点N.易得OF=OA=3,AE=AB-BE=4,∠ABF=∠ACF=∠FCH,⌢BC=⌢BH,所以∠BFC=∠HCB,所以∠BAF=∠BCE=∠HCB+∠FCH=∠BFC+∠ABF=∠AEF,所以AF=EF.易得AN=EN=1/2AE=2,所以ON=AO-AN=1.由勾股定理,可得FN²=OF²-ON²=8,所以AF=√(FN²+AN²)=2√3.

3. 如图,在$\odot O$中,劣弧 AB 的度数为$120^{\circ }$,P 是优弧 AB 上的动点,且不与点 A,B 重合,弦 PB 的垂直平分线分别交射线 PA,弦 PB 于点 C,D.
(1) 求证：△PCB 是等边三角形.

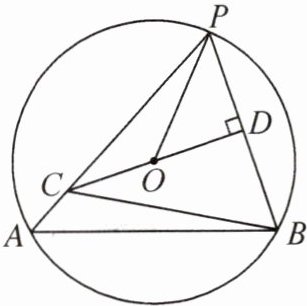
(2) △POC 能否为等腰三角形？如果能,求出此时∠POC 的度数；如果不能,请说明理由.
(3) 若$\odot O$的半径为 2,则△POC 面积的最大值是______.

答案：

(1)证明:连接OA,OB.因为劣弧AB的度数为120°,所以∠AOB=120°,所以∠APB=60°.因为DC是PB的垂直平分线,所以CP=CB.所以△PCB是等边三角形.
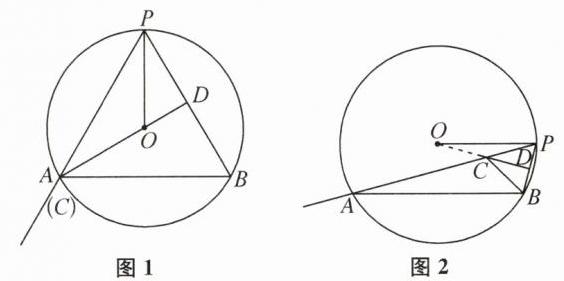
(2)解:①当OC=OP时,如图1.因为OP是⊙O的半径,所以此时OC也是⊙O的半径,点C在⊙O上,易知点C与点A重合.由
(1)可知△PCB是等边三角形,所以∠B=∠PCB=60°,所以∠POC=2∠B=120°.
②当CO=CP时,有两种情况:当点P靠近点B时,如图2.因为CD是PB的垂直平分线,所以点O在直线CD上,即O,C,D三点共线.因为∠PCB=60°,所以∠PCD=30°.因为CO=CP,所以∠POC=15°.当点P靠近点A时,如图3.又因为∠PCB=60°,所以∠PCO=30°.因为CO=CP,所以∠POC=75°.
③当OP=CP时,又因为△PCB为等边三角形,所以CP=BP=OP.又因为OP=OB,所以△OPB为等边三角形,所以∠POB=60°.又因为∠AOB=120°,所以∠POA=180°,即此时点P在AO的延长线上,易知此时点C与点O重合,所以以P,O,C为顶点不构成三角形,故此情况不存在.
综上所述,△POC能为等腰三角形,∠POC的度数为120°或15°或75°.
(3)2+√3 提示:如图4,取⌢AB的中点K,连接AK,BK,CK,OK,OA,OB.因为CD是PB的垂直平分线,所以点O在直线CD上,CP=CB.因为OP=OB,OC=OC,所以△POC≌△BOC,所以S△POC=S△BOC.由△PCB为等边三角形,可得∠CPB=60°=∠PCB.在圆内接四边形APBK中,∠AKB=180°-∠APB=120°.所以点A,B,C在以点K为圆心,AK长为半径的⊙K上.易证△AOK≌△BOK,所以∠AKO=∠BKO=60°.又因为OB=OK=2,所以△OBK为等边三角形,所以AK=BK=OK=2,所以点O在⊙K上.过点C作CJ⊥OB于点J,当点C,K,J依次共线时,CJ的长最大,S△BOC最大,即S△POC最大,此时OJ=BJ=1,∠OKJ=∠BKJ=30°,所以KJ=√(OK²-OJ²)=√3,所以CJ=CK+KJ=2+√3,所以S△BOC=1/2OB·CJ=2+√3.所以△POC面积的最大值为2+√3.