《2025年小题狂做九年级数学上册苏科版巅峰版》

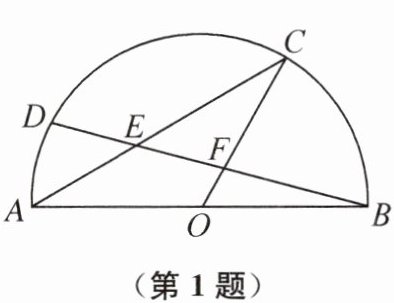
1. 如图,在以点 O 为圆心的半圆中,AB 是直径,$\widehat {AD}+\widehat {BC}= \widehat {CD}$,连接 AC,BD 交于点 E,连接 OC 交 BD 于点 F. 若$CE= \frac {1}{2}AB$,则$CE:CA$的值是( )

A.$\frac {2}{3}$
B.$\frac {\sqrt {2}}{2}$
C.$\frac {3}{4}$
D.$\frac {\sqrt {3}}{3}$
]

答案：
D　提示:如图，连接OD,BC.设∠AOD=x°,∠BOC=y°,∠COD=z°,则x+y+z=180.因为$\widehat {AD}+\widehat {BC}=\widehat {CD}$，所以x+y=z，所以z=90，所以∠COD=90°，所以∠DBC=$\frac{1}{2}$∠COD=45°.因为∠ACB=90°，所以$BC=CE=\frac{1}{2}AB$.在Rt△ABC中，由勾股定理，得$CA=\sqrt {AB^{2}-BC^{2}}=\frac {\sqrt {3}}{2}AB$，所以CE:$CA=\frac {1}{2}AB:\frac {\sqrt {3}}{2}AB=\frac {\sqrt {3}}{3}$.
　　　　　

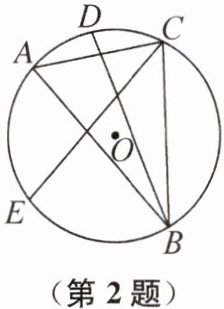
2. 如图,已知$\triangle ABC是\odot O$的内接三角形,$AB≠AC,∠ABC和∠ACB的平分线分别交\odot O$于点 D,E,且$BD= CE$,则$∠BAC$的度数为(B)

A.$90^{\circ }$
B.$60^{\circ }$
C.$45^{\circ }$
D.$30^{\circ }$

答案： B　提示:连接CD,则∠ACD=∠ABD=∠CBD.因为BD=CE，所以$\widehat {CB}=\widehat {DE}$.所以∠BAC=∠DCE=∠ACD+∠ACE=∠ABD+∠ACE.在△ABC中，∠BAC+∠ABC+∠ACB=180°，即∠BAC+2∠ABD+2∠ACE=3∠BAC=180°，所以∠BAC=60°.

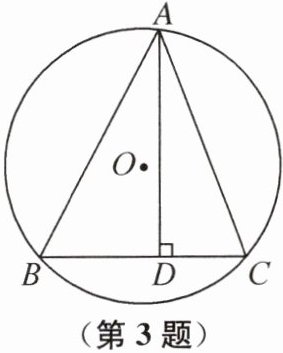
3. 如图,$\triangle ABC内接于\odot O,∠BAC= 45^{\circ },AD⊥BC$,垂足为 D,$BD= 6,DC= 4$,则AB 的长为(D)

A.$6\sqrt {2}$
B.10
C.12
D.$6\sqrt {5}$
]

答案： D　提示:连接OA,OB,OC，过点O分别作OE⊥AD于点E，OF⊥BC于点F，则四边形OFDE为矩形.因为BD=6，DC=4，所以BC=10.因为∠BAC=45°，所以∠BOC=2∠BAC=90°.因为OB=OC，且OF⊥BC，所以$BF=CF=\frac{1}{2}BC=5$，OE=DF=BD−BF=1.易得$OA=OB=\frac {\sqrt {2}}{2}BC=5\sqrt {2}$，$DE=OF=\frac{1}{2}BC=5$.在Rt△AOE中，$AE=\sqrt {OA^{2}-OE^{2}}=7$，所以AD=AE+DE=12，所以$AB=\sqrt {AD^{2}+BD^{2}}=6\sqrt {5}$.

4. 如图,AB,BC 是$\odot O$的弦,$∠B= 60^{\circ }$,点 O在$∠B$内,D 为$\widehat {AC}$上的动点,M,N,P分别是 AD,DC,CB 的中点. 若$\odot O$的半径为2,则$PN+MN$的最大值为(D)
A.$1+\sqrt {3}$
B.$1+2\sqrt {3}$
C.$2+2\sqrt {3}$
D.$2+\sqrt {3}$

答案： D　提示:连接OC,OA,AC,BD，则∠AOC=2∠ABC=120°.过点O作OH⊥AC于点H，易知CH=AH，∠OCA=∠OAC=30°.所以$OH=\frac{1}{2}OC=1$，所以$CH=AH=\sqrt {OC^{2}-OH^{2}}=\sqrt {3}$，所以$AC=2\sqrt {3}$.因为CN=DN，DM=AM，所以$MN=\frac{1}{2}AC=\sqrt {3}$.又因为CP=PB，CN=DN，所以$PN=\frac{1}{2}BD$.当BD是$\odot O$的直径时，BD的值最大，此时PN的值也最大，所以PN的最大值为2.所以PN+MN的最大值为$2+\sqrt {3}$.

5. 如图,在$\odot O$中,C 是$\widehat {AB}$的中点,点 P 在$\widehat {AC}$上,且$∠APB= 120^{\circ },CH⊥BP$于点 H.若$AP= CH$,则$\frac {PH}{HB}= $$\frac{3−\sqrt{3}}{2}$.

答案： $\frac{3−\sqrt{3}}{2}$　提示:在PB上截取MB=AP，连接CM,CB,CP,CA,BA.因为C是$\widehat {AB}$的中点，所以$\widehat {AC}=\widehat {BC}$，所以AC=BC.又因为∠PAC=∠MBC，易证△APC≌△BMC(SAS)，所以CP=CM，所以∠CPM=∠CMP.因为CH⊥PM，所以PH=MH.因为∠ACB=∠APB=120°，所以∠CAB=∠CBA=30°，所以∠CMP=∠CPM=∠CAB=30°，可得$PH=MH=\sqrt {3}CH=\sqrt {3}AP$.所以$BH=MH+MB=(\sqrt {3}+1)AP$.所以$\frac{PH}{BH}=\frac{\sqrt {3}AP}{(\sqrt {3}+1)AP}=\frac{3−\sqrt{3}}{2}$.

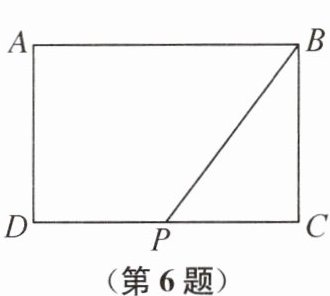
6. 如图,在矩形 ABCD 中,$AD= 4,AB= 6$,P 为CD 的中点,连接 BP. 在矩形 ABCD 内部找一点 E,使得$∠BEC= ∠BPC$,则线段 DE 长的最小值为___.

答案： $\frac{\sqrt{97}−5}{2}$　提示:由∠BEC=∠BPC可知，点E在△BPC的外接圆上，且在矩形ABCD的内部，其中BP的中点(设为点O)为圆心.连接OD,OE，则DE≥OD−OE.所以当E是OD与$\odot O$的交点时，DE有最小值，最小值为$OD−OE=OD-\frac{1}{2}BP$.过点O作OH⊥DC于点H.易得OH是△BPC的中位线，$OH=2$，$PH=\frac{1}{2}PC=\frac{1}{4}DC=\frac{1}{4}AB=\frac{3}{2}$，$DH=DP+PH=\frac{9}{2}$，$OD=\sqrt {OH^{2}+DH^{2}}=\frac {\sqrt {97}}{2}$.因为$BP=\sqrt {BC^{2}+PC^{2}}=5$，所以线段DE长的最小值为$\frac{\sqrt{97}−5}{2}$.

7. 如图,在平面直角坐标系中,$\odot P$的圆心在 x轴上,且经过点$A(m,-3)和点B(-1,n)$,C 是第一象限内圆上的任意一点,且$∠ACB= 45^{\circ }$,则$\odot P$的圆心坐标为(2,0).

答案： (2,0)　提示:连接PB,PA，过点B作BE⊥x轴于点E，过点A作AF⊥x轴于点F.因为点A(m,−3)，B(−1,n)，所以OE=1，AF=3.因为∠ACB=45°，所以∠APB=2∠ACB=90°，易证△BPE≌△PAF，所以PE=AF=3.设点P(a,0)，则a−(−1)=3，所以a=2，所以$\odot P$的圆心坐标为(2,0).

8. 如图,等边三角形 ABC 内接于$\odot O$,D 是$\widehat {ACB}$上的一个动点(不与点 A,B 重合),连接 BD,过点 A 作$AE⊥BD$,垂足为 E,连接 CE. 若$\odot O$的半径为 2,则 CE 长的最小值为$3−\sqrt{3}$.

答案： $3−\sqrt{3}$　提示:连接CO并延长，交AB于点O'，连接OA,O'E.因为△ABC为等边三角形且内接于$\odot O$，所以CO⊥AB，CO'⊥AB，O'A=O'B.又因为AE⊥BD，所以∠AEB=90°，所以点E在以AB为直径的圆弧上运动，且$O'E=\frac{1}{2}AB$.可知CE≥C'O−O'E，所以CE的最小值为C'O−O'E.易得$O'A=\sqrt {3}$，所以$AC=AB=2O'A=2\sqrt {3}$.所以$O'E=\frac{1}{2}AB=\sqrt {3}$.在Rt△AO'C中，由勾股定理，得$CO'=\sqrt {AC^{2}-O'A^{2}}=3$.所以CE的最小值为$CO'-O'E=3-\sqrt {3}$.

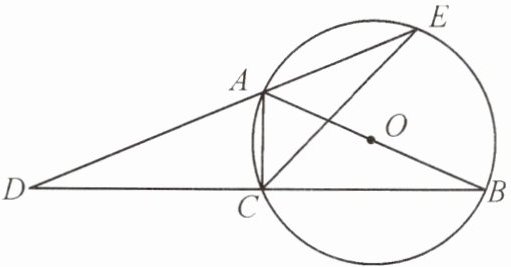
9. 如图,AB 为$\odot O$的直径,点 C 在$\odot O$上,延长 BC 至点 D,使$CD= CB$. 连接 DA并延长,与$\odot O$交于点 E,连接 AC,CE.
(1)求证:$∠B= ∠D.$
(2)若$AB= 4,CB-AC= 2$,求 CE 的长.
]

答案：
(1)证明:因为AB为$\odot O$的直径，所以∠ACB=90°，所以AC⊥BC.又因为CD=CB，所以$AD=\sqrt {CD^{2}+AC^{2}}=\sqrt {CB^{2}+AC^{2}}=AB$，所以∠B=∠D.
(2)解:设CB=x，则AC=x−2.在Rt△ABC中，由勾股定理，得$AC^{2}+CB^{2}=AB^{2}$，即$(x−2)^{2}+x^{2}=4^{2}$，解得$x_1=1+\sqrt {7}$，$x_2=1−\sqrt {7}$(舍去).因为∠B=∠E且∠B=∠D，所以∠D=∠E，所以CD=CE.又因为CD=CB，所以$CE=CB=1+\sqrt {7}$.