《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

29. 如图,在四边形ABCD中,$AB// CD,AD⊥CD,∠B= 45^{\circ }$,延长CD到点E,使$DE= DA$,连接AE.
(1)求证:$AE= BC$;
证明:∵AB//CD,∠B=45°,∴∠C+∠B=180°,∴∠C=135°.∵DE=DA,AD⊥CD,∴∠E=45°.∵∠E+∠C=180°,∴AE//BC,且AB//CD,∴四边形ABCE是平行四边形,∴AE=BC.
(2)若$AB= 3,CD= 1$,求四边形ABCE的面积.
解:∵四边形ABCE是平行四边形,∴AB=CE=3,∴AD=DE=AB−CD=2,∴四边形ABCE的面积=3×2=6.

答案：
(1)证明:
∵AB//CD,∠B=45°,
∴∠C+∠B=180°,
∴∠C=135°.
∵DE=DA,AD⊥CD,
∴∠E=45°.
∵∠E+∠C=180°,
∴AE//BC,且AB//CD,
∴四边形ABCE是平行四边形,
∴AE=BC.
(2)解:
∵四边形ABCE是平行四边形,
∴AB=CE=3,
∴AD=DE=AB−CD=2,
∴四边形ABCE的面积=3×2=6.

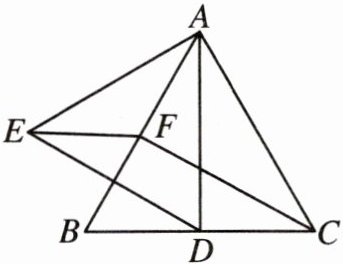
30. 如图,$△ABC$为等边三角形,D,F分别为BC,AB上的点,且$CD= BF$,以AD为边作等边$△ADE$.
(1)求证:$△ACD\cong △CBF$;
(2)点D在线段BC上何处时,四边形CDEF是平行四边形且$∠DEF= 30^{\circ }$?

答案：

(1)证明:
∵△ABC为等边三角形,
∴AC=BC,∠FBC=∠DCA,在△ACD和△CBF中,
$\left\{\begin{array}{l} AC=BC,\\ ∠DCA=∠FBC,\\ CD=BF,\end{array}\right. $
$\therefore \triangle ACD\cong \triangle CBF(SAS)$.
(2)解:当D在线段BC上的中点位置时,四边形CDEF为平行四边形,且∠DEF=30°,按上述条件作图,连接BE,在△AEB和△ADC中,AB=AC,∠EAB+∠BAD=∠DAC+∠BAD=60°,即∠EAB=∠DAC,AE=AD,
∴△AEB≌△ADC(SAS).又
∵△ACD≌△CBF,
∴△AEB≌△ADC≌△CFB,
∴EB=FB,∠EBA=∠ABC=60°,
∴△EFB为等边三角形,
∴BF=FE=CD,∠EFB=60°.又
∵∠ABC=60°,
∴∠EFB=∠ABC=60°,
∴EF//BC,而CD在BC上,
∴EF平行且等于CD,
∴四边形CDEF为平行四边形.
∵点D在线段BC上的中点,
∴点F在线段AB上的中点,
∴∠FCD=$\frac{1}{2}$×60°=30°,则∠DEF=∠FCD=30°.
　　　　　　　　　　　

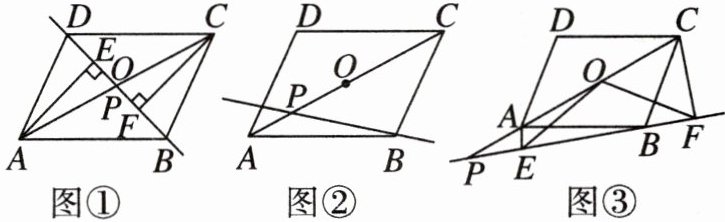
31. 点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F.点O为AC的中点.
(1)如图①,当点P与点O重合时,线段OE和OF的关系是____;
(2)当点P运动到如图②所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立?
(3)如图③,点P在线段OA的延长线上运动,当$∠OEF= 30^{\circ }$时,试探究线段CF,AE,OE之间的关系.

答案：

(1)OE=OF
(2)补全图形如图①，结论仍然成立.证明如下:延长EO交CF于点G.
∵AE⊥BP,CF⊥BP,
∴AE//CF,
∴∠EAO=∠GCO.
∵点O为AC的中点，
∴AO=CO.又
∵∠AOE=∠COG,
∴△AOE≌△COG(ASA),
∴OE=OG,
∴∠GFE=90°,
∴OE=OF.
(3)点P在线段OA的延长线上运动时，线段CF,AE,OE之间的关系为OE=CF十AE.证明如下:如图②，延长EO交FC的延长线于点H,由
(2)可知△AOE≌△COH,
∴AE=CH,OE=OH.又
∵∠OEF=30°,∠HFE=90°,
∴HF=$\frac{1}{2}$EH=OE,
∴OE=CF+CH=CF+AE;