《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

20. (10分)某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米．计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为28米．
(1)这个车棚的长和宽分别为多少米？
答：这个车棚的长为10米，宽为8米。
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米？
答：小路的宽度是1米。

答案： 解:
(1) 设平行于墙的边长为 $x$ 米, 则垂直于墙的边长为 $\frac{28 - x}{2}$ 米, 依题意得 $x \cdot \frac{28 - x}{2} = 80$, 整理得 $x^{2} - 28x + 160 = 0$, 解得 $x_{1} = 8, x_{2} = 20$. 又 $\because$ 已有墙的长度为 12 米, $\therefore x = 8$, $\therefore \frac{28 - x}{2} = 10$. $\therefore$ 这个车棚的长为 10 米, 宽为 8 米.
(2) 设小路的宽度是 $m$ 米, 则停放自行车的区域可合成长为 $(10 - m)$ 米, 宽为 $(8 - 2m)$ 米的长方形, 依题意得 $(10 - m)(8 - 2m) = 54$, 整理得 $m^{2} - 14m + 13 = 0$, 解得 $m_{1} = 1, m_{2} = 13$. 当 $m = 1$ 时, $10 - m = 9, 8 - 2m = 6$; 当 $m = 13$ 时, $10 - m = -3$ (不合题意, 舍去). $\therefore$ 小路的宽度是 1 米.

21. (12分)如图,用同样规格的黑、白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题．

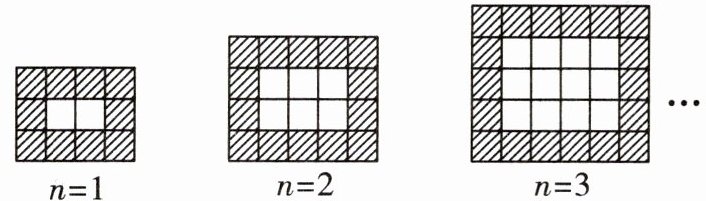
(1)在第n个图中,第一横行共n + 3块瓷砖,第一竖列共有n + 2块瓷砖(均用含n的代数式表示)；
(2)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值；
(3)是否存在黑瓷砖和白瓷砖块数相等的情况？请通过计算说明理由．

答案： 解:
(1) $n + 3$ $n + 2$
(2) 由题意 $(n + 3)(n + 2) = 506$, 解得 $n_{1} = 20, n_{2} = -25$ (舍去), $\therefore n = 20$.
(3) 当黑、白瓷砖块数相等时, 有 $n(n + 1) = (n^{2} + 5n + 6) - n(n + 1)$, 整理得 $n^{2} - 3n - 6 = 0$, 解得 $n_{1} = \frac{3 + \sqrt{33}}{2}, n_{2} = \frac{3 - \sqrt{33}}{2}$, 由于两数均不是整数, 因而不存在两种瓷砖块数相等的情况.

22. (12分)某商店进了一批台灯,每个成本为50元,经过试销发现,若按每个60元出售,可销售800个,销售单价每提高5元,销量就相应减少100个,如果该商店销售这批台灯要获得利润12000元,同时要尽可能让利于顾客,那么这种台灯的售价应定为每个多少元？该商店应进这种台灯多少个？

答案： 解: 设这种台灯的售价应定为每个 $x$ 元, 则可销售 $(800 - \frac{x - 60}{5} \times 100)$ 个, 依题意, 得 $(x - 50)(800 - \frac{x - 60}{5} \times 100) = 12000$, 整理得 $x^{2} - 150x + 5600 = 0$, 解得 $x_{1} = 70, x_{2} = 80$. $\because$ 要尽可能让利于顾客, $\therefore x = 70$, $\therefore 800 - \frac{x - 60}{5} \times 100 = 600$. $\therefore$ 这种台灯的售价应定为每个 70 元, 该商店应进这种台灯 600 个.

23. (14分)晓波超市以每千克42元的价格购进一种干果,计划以每千克60元的价格销售．为了尽可能让利于顾客,现决定降价销售．已知这种干果销售量y(千克)与每千克降价x(元)($0＜x＜18$)之间满足一次函数关系,其图象如图所示．
(1)求y与x之间的函数关系式；
(2)若晓波超市要获利1920元,则这种干果每千克应降价多少元？
(1)设 $y$ 与 $x$ 之间的函数关系式为 $y = kx + b(k \neq 0)$, 将 $(2, 120), (4, 140)$ 代入 $y = kx + b$, 得 $\begin{cases} 120 = 2k + b, \\ 140 = 4k + b, \end{cases}$ 解得 $\begin{cases} k = 10, \\ b = 100, \end{cases}$ $\therefore y$ 与 $x$ 之间的函数关系式为 $y=$$10x + 100$.
(2)依题意得 $(60 - 42 - x)(10x + 100) = 1920$, 整理得 $x^{2} - 8x + 12 = 0$, 解得 $x_{1} = 2, x_{2} = 6$. $\because$ 要尽可能让利于顾客, $\therefore x=$6. $\therefore$ 这种干果每千克应降价6元.

答案： 解:
(1) 设 $y$ 与 $x$ 之间的函数关系式为 $y = kx + b(k \neq 0)$, 将 $(2, 120), (4, 140)$ 代入 $y = kx + b$, 得 $\begin{cases} 120 = 2k + b, \\ 140 = 4k + b, \end{cases}$ 解得 $\begin{cases} k = 10, \\ b = 100, \end{cases}$ $\therefore y$ 与 $x$ 之间的函数关系式为 $y = 10x + 100$.
(2) 依题意得 $(60 - 42 - x)(10x + 100) = 1920$, 整理得 $x^{2} - 8x + 12 = 0$, 解得 $x_{1} = 2, x_{2} = 6$. $\because$ 要尽可能让利于顾客, $\therefore x = 6$. $\therefore$ 这种干果每千克应降价 6 元.