《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

10. (镇江)如图,花瓣图案中的正六边形ABC-DEF的每个内角的度数是$120^{\circ} $.

答案： $ 120^{\circ} $

11. (湖州)为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中$∠A$的度数是____$36^{\circ} $.

答案： $ 36^{\circ} $

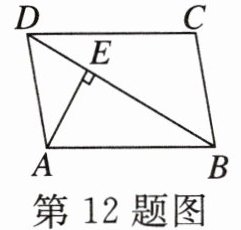
12. (青海)如图,在▱ABCD中,对角线$BD= 8cm,AE⊥BD$,垂足为E,且$AE= 3cm,BC= 4cm$,则AD与BC之间的距离为6 cm.

答案： $ 6 \mathrm{~cm} $

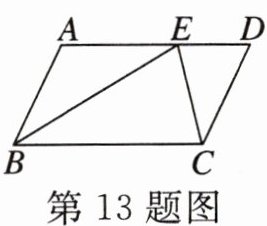
13. (扬州)如图,在▱ABCD中,点E在AD上,且EC平分$∠BED$,若$∠EBC= 30^{\circ },BE= 10$,则$□ ABCD$的面积为50.

答案： 50

14. (贺州)如图,在矩形ABCD中,E,F分别为边BC,DA的中点,以CD为斜边作$Rt△GCD,GD= GC$,连接GE,GF.若$BC= 2GC$,则$∠EGF$的度数为____$45^{\circ} $.

答案： $ 45^{\circ} $

15. (锦州)如图,在矩形ABCD中,$AB= 6,BC= 10$,以点B为圆心、BC的长为半径画弧交AD于点E,再分别以点C,E为圆心、大于$\frac {1}{2}CE$的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为$\frac{10}{3}$.

答案： $ \frac{10}{3} $

16. (苏州)如图,四边形ABCD为菱形,$∠ABC= 70^{\circ }$,延长BC到点E,在$∠DCE$内作射线CM,使得$∠ECM= 15^{\circ }$,过点D作$DF⊥CM$,垂足为F,若$DF= \sqrt {5}$,则对角线BD的长为____$ 2 \sqrt{5} $.

答案： $ 2 \sqrt{5} $

17. (新疆生产建设兵团)如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且$BE= CF$.求证:
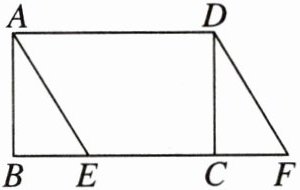
(1)$△ABE\cong △DCF$(SAS);
(2)四边形AEFD是平行四边形.

答案： 证明：
(1) $ \because $ 四边形 $ A B C D $ 是矩形，$ \therefore A B= $ $ C D, \angle B=\angle D C B=90^{\circ}, A D // B C $. $ \because \angle D C B+ $ $ \angle D C F=180^{\circ}, \therefore \angle D C F=\angle B=90^{\circ} $. 在 $ \triangle A B E $ 和 $ \triangle D C F $ 中，$ \left\{\begin{array}{l}A B=D C, \\ \angle B=\angle D C F, \\ B E=C F,\end{array}\right. \therefore \triangle A B E \cong $ $ \triangle D C F(S A S) $.
(2) $ \because B E=C F, \therefore B E+E C=C F+E C $，即 $ B C= $ $ E F $. $ \because $ 四边形 $ A B C D $ 是矩形，$ \therefore A D=B C $，$ \therefore E F=A D $. 又 $ \because A D // B C $，即 $ A D // E F, \therefore $ 四边形 $ A E F D $ 是平行四边形.

18. (邵阳)如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,且$AE= CF$.连接DE,DF,BE,BF.
(1)求证:$△ADE\cong △CBF;$
证明：因为四边形$ABCD$是正方形，所以$AD = CB$，$\angle DAE=\angle BCF = 45^{\circ}$。在$\triangle ADE$和$\triangle CBF$中，$\left\{\begin{array}{l}AD = CB\\\angle DAE=\angle BCF\\AE = CF\end{array}\right.$，根据$SAS$定理，可得$\triangle ADE\cong\triangle CBF$。
(2)若$AB= 4\sqrt {2},AE= 2$,求四边形BEDF的周长.
解：因为四边形$ABCD$是正方形，$AB = 4\sqrt{2}$，根据勾股定理可得$AC=\sqrt{(4\sqrt{2})^{2}+(4\sqrt{2})^{2}}=8$，所以$OA = OB=OC = OD=4$。又因为$AE = CF = 2$，所以$OE=OA - AE=2$，$OF=OC - CF=2$。因为$OB\perp AC$，$OD\perp AC$，$OB = OD$，$OE = OF$，所以四边形$BEDF$是菱形。在$Rt\triangle BOE$中，$BE=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$，所以四边形$BEDF$的周长为$4×2\sqrt{5}=$$8\sqrt{5}$。

答案： 1. （1）证明：
因为四边形$ABCD$是正方形，所以$AD = CB$，$\angle DAE=\angle BCF = 45^{\circ}$。
在$\triangle ADE$和$\triangle CBF$中，$\left\{\begin{array}{l}AD = CB\\\angle DAE=\angle BCF\\AE = CF\end{array}\right.$。
根据$SAS$（边角边）定理，可得$\triangle ADE\cong\triangle CBF$。
2. （2）解：
因为四边形$ABCD$是正方形，$AB = 4\sqrt{2}$，根据勾股定理$AC=\sqrt{AB^{2}+BC^{2}}$（$AB = BC$），则$AC=\sqrt{(4\sqrt{2})^{2}+(4\sqrt{2})^{2}}=\sqrt{32 + 32}=\sqrt{64}=8$。
因为$OA = OB=OC = OD=\frac{1}{2}AC$，所以$OA = OB = OC = OD = 4$。
又因为$AE = CF = 2$，所以$OE=OA - AE=4 - 2 = 2$，$OF=OC - CF=4 - 2 = 2$。
因为$OB\perp AC$，$OD\perp AC$（正方形对角线互相垂直），$OB = OD$，$OE = OF$，所以四边形$BEDF$是菱形（对角线互相垂直且平分的四边形是菱形）。
在$Rt\triangle BOE$中，$OB = 4$，$OE = 2$，根据勾股定理$BE=\sqrt{OB^{2}+OE^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$。
所以四边形$BEDF$的周长$C = 4BE=4×2\sqrt{5}=8\sqrt{5}$。
综上，（1）已证$\triangle ADE\cong\triangle CBF$；（2）四边形$BEDF$的周长为$8\sqrt{5}$。