《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

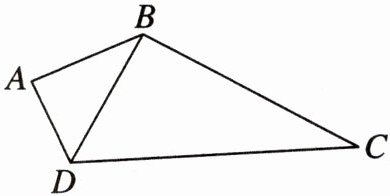
20. (10分)如图,在四边形$ABCD$中,$AB = 4$,$AD = 3$,$AB⊥AD$,$BC = 12$。
(1)求$BD$的长；5
(2)当$CD$为何值时,$\triangle BDC是以CD$为斜边的直角三角形？13
(3)在(2)的条件下,求四边形$ABCD$的面积。36

答案： 解:
(1) $\because AB = 4$，$AD = 3$，$AB ⊥ AD$，$\therefore BD = \sqrt{AD^{2} + AB^{2}} = \sqrt{3^{2} + 4^{2}} = 5$，即 $BD$ 的长是 5。
(2) 在直角 $\triangle BCD$ 中，$BD = 5$，$BC = 12$。$\because CD$ 为斜边，$\therefore CD = \sqrt{BD^{2} + BC^{2}} = \sqrt{5^{2} + 12^{2}} = 13$，$\therefore$ 当 $CD$ 的长为 13 时，$\triangle BDC$ 为直角三角形。
(3) $S_{四边形ABCD} = S_{\triangle ABD} + S_{\triangle BCD} = \frac{1}{2}AB \cdot AD + \frac{1}{2}BD \cdot BC = \frac{1}{2}×4×3 + \frac{1}{2}×5×12 = 36$，$\therefore$ 四边形 $ABCD$ 的面积是 36。

21. (12分)在一棵树的10m高处($D$处)有两只猴子,如图,其中一只猴子爬下树走到离树20m的池塘$A$处,另一只猴子爬到树顶后直接一跃,跳到池塘$A$处(假设沿直线跳跃),如果两只猴子所经过的路程相等,则这棵树有多高？
解:设树高为 $x m$，则 $CD = (x - 10)m$，由题意可知 $BD + AB = 10 + 20 = 30(m)$，$\therefore AC = 30 - CD = 30 - (x - 10) = (40 - x)m$。$\because \triangle ABC$ 为直角三角形，$\therefore AC^{2} = AB^{2} + BC^{2}$，即 $(40 - x)^{2} = 20^{2} + x^{2}$，解得 $x = $15，即树高为 15 m。

答案： 解:设树高为 $x m$，则 $CD = (x - 10)m$，由题意可知 $BD + AB = 10 + 20 = 30(m)$，$\therefore AC = 30 - CD = 30 - (x - 10) = (40 - x)m$。$\because \triangle ABC$ 为直角三角形，$\therefore AC^{2} = AB^{2} + BC^{2}$，即 $(40 - x)^{2} = 20^{2} + x^{2}$，解得 $x = 15$，即树高为 15 m。

22. (12分)如图,在$Rt\triangle ABC$中,$∠B = 90^{\circ}$,$AB = 6cm$,$BC = 10cm$,点$P从点A开始沿AB边向点B$移动,速度为$1cm/s$；点$Q从点B开始沿BC边向点C$移动,速度为$2cm/s$,点$P$,$Q分别从点A$,$B$同时出发,当其中一点到达终点后,另一点也随之停止运动。
(1)几秒后,$PQ的长度为3\sqrt{5}cm$？
答：3秒后，$PQ$的长度为$3\sqrt{5}cm$。
(2)几秒后,$\triangle PBQ的面积为8cm^{2}$？
答：2秒或4秒后，$\triangle PBQ$的面积为$8cm^{2}$。
(3)$\triangle PBQ的面积能不能是14cm^{2}$？请说明理由。
答：$\triangle PBQ$的面积不能是$14cm^{2}$。理由如下：当$S_{\triangle PQB} = 14cm^{2}$时，$\frac{1}{2}BP × BQ = 14$，即$\frac{1}{2}(6 - t) \cdot 2t = 14$，整理得$t^{2} - 6t + 14 = 0$。$\because \Delta = (-6)^{2}-4×1×14 = 36 - 56 = -20 ＜ 0$，$\therefore$方程没有实数根，$\therefore \triangle PQB$的面积不能等于$14cm^{2}$。

答案： 解:设点 $P$，$Q$ 的运动时间为 $t$ 秒，则 $0 ≤ t ≤ 5$，$AP = t cm$，$BP = (6 - t)cm$，$BQ = 2t cm$。
(1) 由勾股定理，得 $BP^{2} + BQ^{2} = PQ^{2} = (3\sqrt{5})^{2} = 45$，即 $(6 - t)^{2} + (2t)^{2} = 45$，解得 $t = 3$ 或 $t = -\frac{3}{5}$（舍去）。故 3 秒后，$PQ$ 的长度为 $3\sqrt{5}cm$。
(2) 由 $S_{\triangle PBQ} = \frac{1}{2}BP × BQ$，得 $8 = \frac{1}{2}(6 - t) \cdot 2t$，解得 $t = 2$ 或 $t = 4$。故 2 秒或 4 秒后，$\triangle PBQ$ 的面积为 $8cm^{2}$。
(3) 当 $S_{\triangle PQB} = 14cm^{2}$ 时，$\frac{1}{2}BP × BQ = 14$，即 $\frac{1}{2}(6 - t) \cdot 2t = 14$，整理得 $t^{2} - 6t + 14 = 0$。$\because \Delta = (-6)^{2}-4\times1\times14 = 36 - 56 = -20 ＜ 0$，$\therefore$ 方程没有实数根，$\therefore \triangle PQB$ 的面积不能等于 $14cm^{2}$。

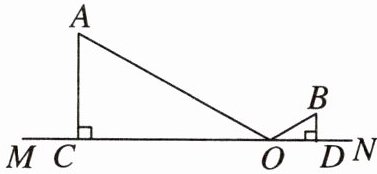
23. (14分)如图,点$A$,$B在直线MN$的同侧,分别过点$A$,$B作AC⊥MN$,$BD⊥MN$,垂足分别为$C$,$D$。已知$AC = 6$,$BD = 1$,$CD = 24$。
(1)设$OC = m$,请用含$m的代数式表示OA + OB$；
(2)求$OA + OB$的最小值。

答案：
解:
(1) 在 $Rt\triangle AOC$ 和 $Rt\triangle BOD$ 中，$OC = m$，则 $OD = 24 - m$，根据勾股定理，得 $OA = \sqrt{AC^{2} + OC^{2}} = \sqrt{36 + m^{2}}$，$OB = \sqrt{OD^{2} + BD^{2}} = \sqrt{(24 - m)^{2} + 1}$，$\therefore OA + OB = \sqrt{36 + m^{2}} + \sqrt{(24 - m)^{2} + 1}$。
(2) 以直线 $MN$ 为对称轴，作点 $B$ 关于 $MN$ 的对称点 $B'$，连接 $AB'$ 交 $MN$ 于点 $O$，则 $OA + OB = OA + OB' = AB'$，此时 $OA + OB$ 最小。过点 $B'$ 作 $B'E ⊥ AC$，交 $AC$ 的延长线于点 $E$，则 $AE = AC + CE = 6 + 1 = 7$，$B'E = CD = 24$。根据勾股定理，得 $AB' = \sqrt{AE^{2} + B'E^{2}} = \sqrt{7^{2} + 24^{2}} = 25$，$\therefore OA + OB$ 的最小值为 25。