《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

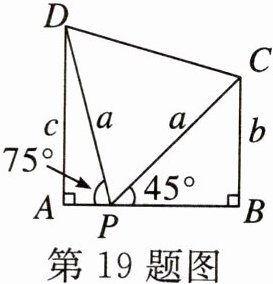
19.如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角$∠BPC为45^{\circ }$;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角$∠APD为75^{\circ }$,则AB的长等于 (D)

A.a
B.b
C.$\frac {b+c}{2}$
D.c

答案： D

20.(柳州)如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连接AC并延长到点D,使$CD= CA$,连接BC并延长到点E,使$CE= CB$,连接DE,那么量出DE的长就是A,B的距离,为什么? 请结合解题过程,完成本题的证明.
证明:在$△DEC和△ABC$中,$\left\{\begin{array}{l} CD= (AC),\\ (∠DCE=∠ACB),\\ CE= (BC),\end{array}\right. $$\therefore △DEC\cong △ABC(SAS),\therefore $______DE=AB.

答案： $ A C $ $ \angle D C E = \angle A C B $ $ B C $ $ D E = A B $

21.某段河流的两岸是平行的,数学兴趣小组在老师的带领下不用涉水过河就测得了两岸的宽度,他们是这样做的:

①河岸的一点B正对着河对岸的一棵树A;
②沿河岸从B处向前直走20 m有一棵树C,继续前行20 m到达D处;
③从D处沿垂直河岸的方向行走,当到达树A正好被树C遮挡住的E处停止行走;
④测得DE的长为5 m.
(1)两岸的宽度是______m;
(2)请你说明他们做法的正确性.
(1) 5
(2) 解：由题意知，在$ R t \triangle A B C $和$ R t \triangle E D C $中，$ \left\{ \begin{array} { l } { \angle A B C = \angle E D C = 90 ^ { \circ } }, \\ { B C = D C }, \\ { \angle A C B = \angle E C D }, \end{array} \right. $ $ \therefore R t \triangle A B C \cong R t \triangle E D C ( A S A ) $，$ \therefore A B = E D $。即他们的做法是正确的。

答案：
(1) 5
(2) 解：由题意知，在$ R t \triangle A B C $和$ R t \triangle E D C $中，$ \left\{ \begin{array} { l } { \angle A B C = \angle E D C = 90 ^ { \circ } }, \\ { B C = D C }, \\ { \angle A C B = \angle E C D }, \end{array} \right. $ $ \therefore R t \triangle A B C \cong R t \triangle E D C ( A S A ) $，$ \therefore A B = E D $。即他们的做法是正确的。

22.如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处,测得商业大厦顶部N的仰角$∠1$的度数,由于楼下植物的遮挡,不能在B处测得商业大厦底部M的俯角的度数.于是,他俩上楼来到小华家,在窗台C处测得大厦底部M的俯角$∠2$的度数,竟然发现$∠1与∠2$恰好相等.已知A,B,C三点共线,$CA⊥AM,NM⊥AM,AB= 31m,BC= 18m$,试求商业大厦的高MN.

答案：
解：如图，过点$ C $作$ C E \perp M N $于点$ E $，过点$ B $作$ B F \perp M N $于点$ F $，$ \therefore \angle C E F = \angle B F E = 90 ^ { \circ } $。$ \because C A \perp A M $，$ N M \perp A M $，$ \therefore $四边形$ A M E C $和四边形$ A M F B $均为矩形，$ \therefore C E = B F $，$ M E = A C $。$ \because \angle 1 = \angle 2 $，$ \therefore \triangle B F N \cong \triangle C E M ( A S A ) $，$ \therefore N F = E M = A C = 31 + 18 = 49 ( m ) $，由矩形性质可知$ E F = C B = 18 m $，$ \therefore M N = N F + E M - E F = 49 + 49 - 18 = 80 ( m ) $。$ \therefore $商业大厦的高$ M N $为$ 80 m $。