2025年暑假总动员八年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员八年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
10. 在学校数学竞赛中,某校10名学生参赛成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是(
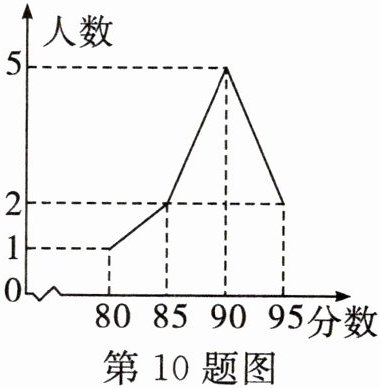
A. 众数是90
B. 中位数是85
C. 平均数是89
D. 最大值与最小值的差是15
B
)
A. 众数是90
B. 中位数是85
C. 平均数是89
D. 最大值与最小值的差是15
答案:
B
11. 数据120,200,100,150,125,80,100的平均数是
125
,众数是100
,中位数是120
。
答案:
125 100 120
12. 某校500名学生参加生命安全知识测试,测试分数均大于或等于60且小于100,分数段的频率分布情况如下表(其中每个分数段包括最小值,不包括最大值),结合表格的信息,可得测试分数在80~90分数段的学生有
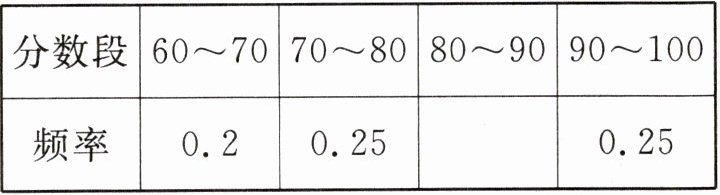
150
名。
答案:
150
13. 对甲、乙两车间生产的某种产品抽样测量,其平均数、方差如下:$\overline{x}_{甲}= 12$,$s^{2}_{甲}= 0.075$,$\overline{x}_{乙}= 12$,$s^{2}_{乙}= 0.100$。
(1)甲车间比乙车间波动
(2)
(1)甲车间比乙车间波动
小
;(2)
甲
车间比乙
车间好。
答案:
(1)小
(2)甲 乙
(1)小
(2)甲 乙
14. 若$a_{1}$,$a_{2}$,…,$a_{20}$这20个数据的平均数为$\overline{x}$,方差为0.20,则数据$a_{1}$,$a_{2}$,…,$a_{20}$,$\overline{x}$这21个数据的方差是
0.19
。
答案:
0.19
15. (8分)甲、乙两台机床在相同的技术条件下同时生产一种零件,现在从中抽测10个,它们的尺寸(单位:mm)分别如下:
甲机床:10.2,10.1,10,9.8,9.9,10.3,9.7,10,9.9,10.1;
乙机床:10.3,10.4,9.6,9.9,10.1,10.9,8.9,9.7,10.2,10。
分别计算上面两个样本的平均数和方差。如果规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?
甲机床:10.2,10.1,10,9.8,9.9,10.3,9.7,10,9.9,10.1;
乙机床:10.3,10.4,9.6,9.9,10.1,10.9,8.9,9.7,10.2,10。
分别计算上面两个样本的平均数和方差。如果规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?
答案:
解:甲:平均数 10 mm,方差 0.03 mm²;乙:平均数 10 mm,方差 0.258 mm². 让甲机床加工这种零件较合适.
16. (8分)学校准备推荐一位老师参加业务技能比赛,对甲、乙两位老师进行三项测试,他们各自的成绩(百分制)如下表:
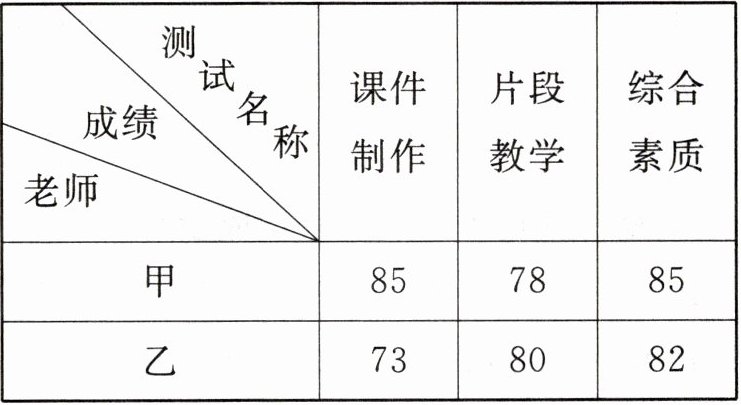
|测试名称成绩老师|课件制作|片段教学|综合素质|
|----|----|----|----|
|甲|85|78|85|
|乙|73|80|82|
学校将课件制作、片段教学、综合素质按2:3:5确定最终成绩,并根据成绩择优推荐,请你通过计算说明谁将被推荐参加比赛。
解:老师甲的最终成绩为 $\frac{85×2 + 78×3 + 85×5}{2 + 3 + 5} = $

|测试名称成绩老师|课件制作|片段教学|综合素质|
|----|----|----|----|
|甲|85|78|85|
|乙|73|80|82|
学校将课件制作、片段教学、综合素质按2:3:5确定最终成绩,并根据成绩择优推荐,请你通过计算说明谁将被推荐参加比赛。
解:老师甲的最终成绩为 $\frac{85×2 + 78×3 + 85×5}{2 + 3 + 5} = $
82.9
(分),老师乙的最终成绩为 $\frac{73×2 + 80×3 + 82×5}{2 + 3 + 5} = $79.6
(分). $\because$82.9>79.6
, $\therefore$ 老师甲
将被推荐参加比赛.
答案:
解:老师甲的最终成绩为 $\frac{85×2 + 78×3 + 85×5}{2 + 3 + 5} = 82.9$ (分),老师乙的最终成绩为 $\frac{73×2 + 80×3 + 82×5}{2 + 3 + 5} = 79.6$ (分). $\because 82.9 > 79.6$, $\therefore$ 老师甲将被推荐参加比赛.
17. (8分)甲、乙两台编织机同时编织一种毛衣,在5天中,两台编织机每天生产出的合格品数量如下(单位:件)。
甲:10,8,7,7,8;乙:9,8,7,7,9。
通过计算说明在这5天中哪台编织机生产出合格品的波动较小。
甲:10,8,7,7,8;乙:9,8,7,7,9。
通过计算说明在这5天中哪台编织机生产出合格品的波动较小。
答案:
解: $\overline{x}_{甲} = \frac{1}{5}×(10 + 8 + 7 + 7 + 8) = 8$ (件), $\overline{x}_{乙} = \frac{1}{5}×(9 + 8 + 7 + 7 + 9) = 8$ (件). $s^{2}_{甲} = \frac{1}{5}×[(10 - 8)^{2} + 2×(8 - 8)^{2} + 2×(7 - 8)^{2}] = 1.2$, $s^{2}_{乙} = \frac{1}{5}×[2×(9 - 8)^{2} + (8 - 8)^{2} + 2×(7 - 8)^{2}] = 0.8$, 因为 $s^{2}_{甲} > s^{2}_{乙}$, 所以乙编织机生产出合格品的波动较小.
查看更多完整答案,请扫码查看


