《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

18. (8分)为保护环境,“赤子之心”环保公益中心组织1000名学生参加义务收集废旧电池的活动,下面随机抽取50名学生对收集的废旧电池数量进行统计：

(1)上述数据中,收集废旧电池节数的众数是4节,中位数是4.5节；
(2)估计这次活动中,1000名学生共收集废旧电池4800节。

答案： 解:
(1)4 4.5
(2)50 名学生共收集废旧电池的平均数为 $(10×3 + 15×4 + 12×5 + 7×6 + 6×8)÷50 = 4.8$ (节), $4.8×1000 = 4800$ (节). 所以估计这 1000 名学生共收集废旧电池 4800 节.

19. (10分)教育部发布的义务教育质量监测结果报告显示,我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%。某校数学社团成员采用简单随机抽样的方法,抽取了本校八年级50名学生,对他们一周内平均每天的睡眠时间t(单位：小时)进行了调查,将数据整理后绘制成下表：

该样本中学生平均每天的睡眠时间达9小时及以上的比例高于全国的这项数据,达到了22%。
(1)求表格中n的值；
(2)该校八年级共400名学生,估计其中平均每天的睡眠时间在7≤t＜8这个范围内的人数是多少。
(1)11
(2)72

答案： 解:
(1) $n = 50×22\% = 11$.
(2) $m = 50 - 1 - 5 - 24 - 11 = 9$ (人), 所以估计该校八年级学生平均每天的睡眠时间在 $7 ≤ t ＜ 8$ 这个范围内的人数是 $400×\frac{9}{50} = 72$ (人).

20. (10分)某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示：

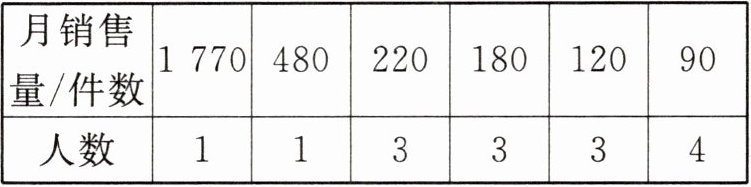
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数；
平均数为278件，中位数为180件，众数为90件。
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标？请说明理由。(提示：目标不宜过高或过低)
中位数最适合作为月销售目标。理由如下: 在这15人中, 月销售不低于278(平均数)件的有2人, 月销售量不低于180(中位数)件的有8人, 月销售量不低于90(众数)件的有15人. 所以, 如果想让一半左右的营业员都能够达到月销售目标, (1)中的平均数、中位数、众数中, 中位数最适合作为月销售目标.

答案： 解:
(1)这 15 名营业员该月销售量数据的平均数 $= \frac{1770 + 480 + 220×3 + 180×3 + 120×3 + 90×4}{15} = 278$ (件), 中位数为 180 件. $\because 90$ 出现了 4 次, 出现的次数最多, $\therefore$ 众数是 90 件.
(2)中位数最适合作为月销售目标. 理由如下: 在这 15 人中, 月销售不低于 278(平均数)件的有 2 人, 月销售量不低于 180(中位数)件的有 8 人, 月销售量不低于 90(众数)件的有 15 人. 所以, 如果想让一半左右的营业员都能够达到月销售目标,
(1)中的平均数、中位数、众数中, 中位数最适合作为月销售目标.

21. (12分)甲、乙两人在“定位投篮”选拔赛测试中(共10轮,每轮投10个球)成绩如图：

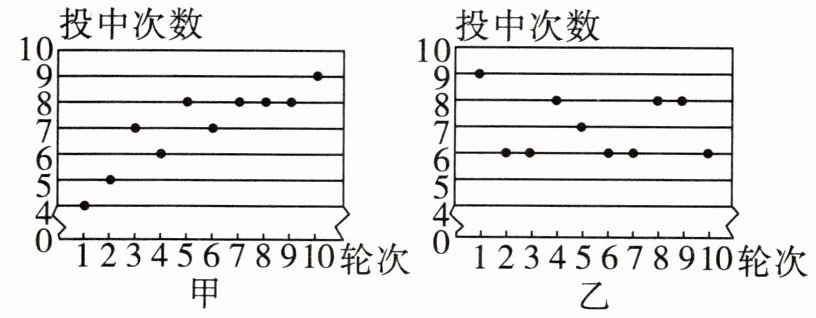
(1)填表：

甲的平均数7，甲的方差2.2，乙的中位数6.5，乙的众数6
(2)如果你是教练,你会选择谁参加正式比赛？请说明理由。
选择甲参加比赛. 理由如下: ∵甲、乙的平均成绩相同, 而甲成绩的中位数大于乙, ∴甲成绩的高分次数多于乙, ∴选择甲参加比赛(答案不唯一, 合理均可).

答案： 解:
(1)7 2.2 6.5 6
(2)选择甲参加比赛. 理由如下: $\because$ 甲、乙的平均成绩相同, 而甲成绩的中位数大于乙, $\therefore$ 甲成绩的高分次数多于乙, $\therefore$ 选择甲参加比赛(答案不唯一, 合理均可).