2025年暑假总动员八年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员八年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
知识点1 认识勾股定理
直角三角形两条直角边的①
直角三角形两条直角边的①
平方和
等于斜边的②平方
.我国古代把直角三角形中较短的直角边称为③勾
,较长的直角边称为④股
,斜边称为⑤弦
,因此,上述定理称为⑥勾股
定理,国外称为毕达哥拉斯定理.
答案:
①平方和 ②平方 ③勾 ④股 ⑤弦 ⑥勾股
知识点2 勾股定理的应用
如图,在△ABC中,∠C= 90°.
(1)若已知a,b,则斜边c=
(2)若已知a,c,则b=
(3)若已知b,c,则a=
(4)若已知a= b,则斜边c= ⑩
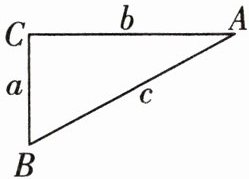
如图,在△ABC中,∠C= 90°.
(1)若已知a,b,则斜边c=
$\sqrt{a^{2}+b^{2}}$
(2)若已知a,c,则b=
$\sqrt{c^{2}-a^{2}}$
(3)若已知b,c,则a=
$\sqrt{c^{2}-b^{2}}$
(4)若已知a= b,则斜边c= ⑩
$\sqrt{2}$
a= ⑪$\sqrt{2}$
b.
答案:
⑦$\sqrt{a^{2}+b^{2}}$ ⑧$\sqrt{c^{2}-a^{2}}$ ⑨$\sqrt{c^{2}-b^{2}}$ ⑩$\sqrt{2}$ ⑪$\sqrt{2}$
知识点3 勾股定理的逆定理
1.内容:如果三角形两边的⑫
2.应用:判定一个三角形是直角三角形.
1.内容:如果三角形两边的⑫
平方和
等于第三边的⑬平方
,那么这个三角形是⑭直角
三角形.2.应用:判定一个三角形是直角三角形.
答案:
⑫平方和 ⑬平方 ⑭直角
知识点4 勾股数
能够成为直角三角形三条边长度的三个⑮
【拓展】勾股数的几种形式
(1)若n为大于1的整数,则$a= n^2-1,b= 2n,c= n^2+1$是勾股数.
(2)若n为正整数,则$a= 2n+1,b= 2n^2+2n,c= 2n^2+2n+1$是勾股数.
(3)若m>n,m,n为正整数,则$a= m^2-n^2,b= 2mn,c= m^2+n^2$是勾股数.
(4)一组勾股数中的各数同时扩大相同的整数倍能得到一组新的勾股数,即若a,b,c是一组勾股数,则ka,kb,kc(k为正整数)也是勾股数.
(5)若最小的数a为奇数,且满足$a^2= b+c(b,c$为连续的正整数),则a,b,c就是一组勾股数,如7,24,25等.
(6)若最小的数a为大于4的偶数,把a除以2再平方,这个平方数各加减1得到两个正整数b,c,则a,b,c就是一组勾股数.如6,8,10;8,15,17等.
能够成为直角三角形三条边长度的三个⑮
正整数
,称为勾股数,如3,4,⑯5
;5,⑰12
,13等.【拓展】勾股数的几种形式
(1)若n为大于1的整数,则$a= n^2-1,b= 2n,c= n^2+1$是勾股数.
(2)若n为正整数,则$a= 2n+1,b= 2n^2+2n,c= 2n^2+2n+1$是勾股数.
(3)若m>n,m,n为正整数,则$a= m^2-n^2,b= 2mn,c= m^2+n^2$是勾股数.
(4)一组勾股数中的各数同时扩大相同的整数倍能得到一组新的勾股数,即若a,b,c是一组勾股数,则ka,kb,kc(k为正整数)也是勾股数.
(5)若最小的数a为奇数,且满足$a^2= b+c(b,c$为连续的正整数),则a,b,c就是一组勾股数,如7,24,25等.
(6)若最小的数a为大于4的偶数,把a除以2再平方,这个平方数各加减1得到两个正整数b,c,则a,b,c就是一组勾股数.如6,8,10;8,15,17等.
答案:
⑮正整数 ⑯5 ⑰12
1. (陕西)如图, 在 $ 3 × 3 $ 的网格中, 每个小正方形的边长均为 1, 点 $ A, B, C $ 都在格点上, 若 $ B D $ 是 $ \triangle A B C $ 的高, 则 $ B D $ 的长为 (
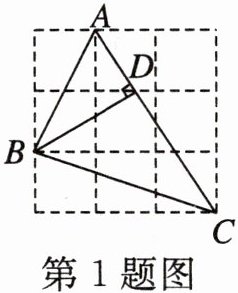
A. $ \frac{10}{13} \sqrt{13} $
B. $ \frac{9}{13} \sqrt{13} $
C. $ \frac{8}{13} \sqrt{13} $
D. $ \frac{7}{13} \sqrt{13} $
D
)
A. $ \frac{10}{13} \sqrt{13} $
B. $ \frac{9}{13} \sqrt{13} $
C. $ \frac{8}{13} \sqrt{13} $
D. $ \frac{7}{13} \sqrt{13} $
答案:
D
2. (新疆)如图, 在 $ \mathrm{Rt} \triangle A B C $ 中, $ \angle A C B= 90^{\circ} $, $ \angle A= 30^{\circ}, A B= 4, C D \perp A B $ 于点 $ D, E $ 是 $ A B $ 的中点, 则 $ D E $ 的长为 (
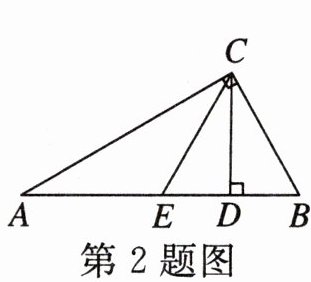
A. 1
B. 2
C. 3
D. 4
A
)
A. 1
B. 2
C. 3
D. 4
答案:
A
查看更多完整答案,请扫码查看


