《2025年暑假总动员八年级数学沪科版合肥工业大学出版社》

24. 一块正方形的瓷砖,面积为$50\mathrm{cm}^{2}$,它的边长大约在 (D)
A. $4\sim 5\mathrm{cm}$之间
B. $5\sim 6\mathrm{cm}$之间
C. $6\sim 7\mathrm{cm}$之间
D. $7\sim 8\mathrm{cm}$之间

答案： D

25. 某小区有一块长方形的草地,这块草地的宽为$(\sqrt{6}-\sqrt{2})\mathrm{m}$,为美化小区环境,给这块长方形草地围上白色的低矮栅栏,所需的栅栏的长度为$(10\sqrt{6}-2\sqrt{2})\mathrm{m}$,那么这块草地的面积为 (B)
A. $24\mathrm{m}^{2}$
B. $(24 - 8\sqrt{3})\mathrm{m}^{2}$
C. $48\mathrm{m}^{2}$
D. $(48 - 16\sqrt{3})\mathrm{m}^{2}$

答案： B

26. 在日常生活中,取款、上网都要密码.为了保密,有人发明了“二次根式法”来生成密码,如对于二次根式$\sqrt{169}$,计算结果为$13$,中间加一个数字$0$,于是就得到一个六位数的密码“169013”,对于二次根式$\sqrt{0.25}$,用上述方法生成的六位数密码是025005.

答案： 025005

27. 某同学在作业本上做了这样一道题:“当$a = $●时,试求$(\sqrt{a})^{2}+\sqrt{a^{2}-2a + 1}$的值”.其中,●是被墨水弄污的,该同学求得的答案为$\dfrac{1}{2}$,该同学的答案是否正确?请说明理由.

答案： 解：该同学的答案不正确. 理由如下：$(\sqrt{a})^2 +\sqrt{a^2 - 2a + 1} = a + |a - 1|$. ①当 $a \geq 1$ 时，原式 $= a +a - 1 = 2a - 1 \geq 1$；②当 $0 \leq a ＜ 1$ 时，原式 $= a - a +1 = 1, \therefore$ 在满足条件的范围内，无论 $a$ 取何值，原式都是大于等于 1 的，不可能为 $\frac{1}{2}, \therefore$ 该同学的答案不正确.

28. 如图,将一块面积为$30\mathrm{m}^{2}$的大正方形铁皮的四个角各截去一个面积为2$\mathrm{m}^{2}$的小正方形,剩下的部分刚好能围成一个无盖的长方体运输箱,求此运输箱底面的边长.(精确到$0.1\mathrm{m}$,参考数据:$\sqrt{30}\approx 5.477$,$\sqrt{2}\approx 1.414$)

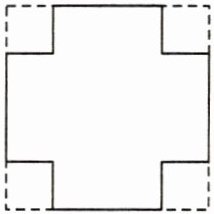
解：大正方形的边长为 $\sqrt{30}m$，小正方形的边长为 $\sqrt{2}m, \therefore$ 运输箱底面的边长为 $\sqrt{30} - 2 ×\sqrt{2} \approx$2.6$(m), \therefore$ 此运输箱底面的边长约为2.6$m$.

答案： 解：大正方形的边长为 $\sqrt{30}m$，小正方形的边长为 $\sqrt{2}m, \therefore$ 运输箱底面的边长为 $\sqrt{30} - 2 \times\sqrt{2} \approx 2.6(m), \therefore$ 此运输箱底面的边长约为 $2.6m$.

29. 据研究,高空抛物下落的时间$t$(单位:$\mathrm{s}$)和高度$h$(单位:$\mathrm{m}$)近似满足关系式$t = \sqrt{\dfrac{h}{5}}$(不考虑风速的影响).
(1)求从$40\mathrm{m}$高空抛物到落地的时间;$2\sqrt{2}\ \text{s}$
(2)小明说从$80\mathrm{m}$高空抛物到落地的时间是(1)中所求时间的$2$倍,他的说法正确吗?如果不正确,请说明理由;不正确. 理由如下：当$h = 80\mathrm{m}$时，$t=\sqrt{\dfrac{80}{5}}=\sqrt{16}=4(\mathrm{s})$. $\because 4\neq2×2\sqrt{2}$，$\therefore$小明的说法不正确
(3)已知高空坠落物体的动能$ = 10×物体质量×$高度(单位:$\mathrm{J}$),某质量为$0.05\mathrm{kg}$的鸡蛋经过$6\mathrm{s}$落在地上,这个鸡蛋产生的动能是多少?你能得到什么启示?(注:杀伤无防护人体只需要$65\mathrm{J}$的动能)$90\ \text{J}$；启示：严禁高空抛物，否则会对人体造成损伤（合理即可）

答案： 解：
(1)由题意知 $h = 40m, t = \sqrt{\frac{h}{5}} = \sqrt{\frac{40}{5}} =\sqrt{8} = 2\sqrt{2}(s)$.
(2)不正确. 理由如下：当 $h = 80m$ 时，$t = \sqrt{\frac{80}{5}} =\sqrt{16} = 4(s). \because 4 \neq 2 \times 2\sqrt{2}, \therefore$ 小明的说法不正确.
(3)当 $t = 6s$ 时，$6 = \sqrt{\frac{h}{5}}$，解得 $h = 180m$，鸡蛋产生的动能 $= 10 \times 0.05 \times 180 = 90(J)$. 启示：严禁高空抛物，否则会对人体造成损伤. (合理即可)