第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
3. 解方程或解比例。
$(10+x)×7= 714$ $\frac {2}{3}x+\frac {1}{6}x= 25$
$\frac {1}{17}:x= 0.2:51$
$(10+x)×7= 714$ $\frac {2}{3}x+\frac {1}{6}x= 25$
$\frac {1}{17}:x= 0.2:51$
答案:
解析:
第一题考查的是一元一次方程的解法,需要先将方程展开,然后移项求解。
第二题考查的是分数方程的解法,需要找到公分母,然后合并同类项求解。
第三题考查的是比例方程的解法,需要利用内项之积等于外项之积的原则求解。
答案:
(1)解:$(10+x)×7=714$,
去括号得:$70+7x=714$,
移项得:$7x=714-70$,
合并同类项得:$7x=644$,
系数化为1得:$x=92$。
(2)解:$\frac{2}{3}x+\frac{1}{6}x=25$,
合并同类项得:$\frac{4}{6}x+\frac{1}{6}x=25$,
即:$\frac{5}{6}x=25$,
系数化为1得:$x=25×\frac{6}{5}$,
解得:$x=30$。
(3)解:$\frac{1}{17}:x=0.2:51$,
根据内项之积等于外项之积得:$0.2x=51×\frac{1}{17}$,
即:$0.2x=3$,
系数化为1得:$x=3÷0.2$,
解得:$x=15$。
第一题考查的是一元一次方程的解法,需要先将方程展开,然后移项求解。
第二题考查的是分数方程的解法,需要找到公分母,然后合并同类项求解。
第三题考查的是比例方程的解法,需要利用内项之积等于外项之积的原则求解。
答案:
(1)解:$(10+x)×7=714$,
去括号得:$70+7x=714$,
移项得:$7x=714-70$,
合并同类项得:$7x=644$,
系数化为1得:$x=92$。
(2)解:$\frac{2}{3}x+\frac{1}{6}x=25$,
合并同类项得:$\frac{4}{6}x+\frac{1}{6}x=25$,
即:$\frac{5}{6}x=25$,
系数化为1得:$x=25×\frac{6}{5}$,
解得:$x=30$。
(3)解:$\frac{1}{17}:x=0.2:51$,
根据内项之积等于外项之积得:$0.2x=51×\frac{1}{17}$,
即:$0.2x=3$,
系数化为1得:$x=3÷0.2$,
解得:$x=15$。
1. 在下面两幅图中分别用阴影表示出$\frac {4}{9}$千克。


答案:


2.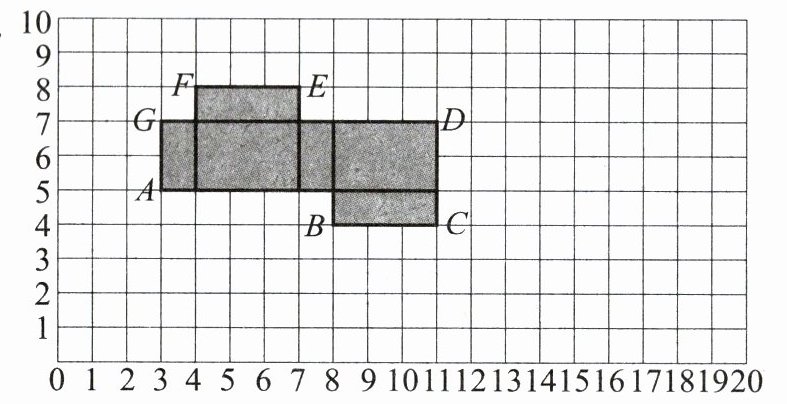
(1) 图中的阴影部分是一个长方体的平面展开图,如果把它折成长方体,那么点F、点G和点( )重合。如果每个小方格的边长是1厘米,那么这个长方体的表面积是( )平方厘米,体积是( )立方厘米。
(2) 如果把线段CD向右平移5格,再向下平移4格,那么平移后点D的位置用数对表示是( , )。
(3) 先以点A为圆心,画一个半径为2厘米的圆。再算一算,这个圆与长方体的平面展开图(即阴影部分)重叠部分的面积是( )平方厘米。(结果保留π)

(1) 图中的阴影部分是一个长方体的平面展开图,如果把它折成长方体,那么点F、点G和点( )重合。如果每个小方格的边长是1厘米,那么这个长方体的表面积是( )平方厘米,体积是( )立方厘米。
(2) 如果把线段CD向右平移5格,再向下平移4格,那么平移后点D的位置用数对表示是( , )。
(3) 先以点A为圆心,画一个半径为2厘米的圆。再算一算,这个圆与长方体的平面展开图(即阴影部分)重叠部分的面积是( )平方厘米。(结果保留π)
答案:
解析:本题主要考查长方体的展开图、平移、圆与长方体平面展开图重叠部分面积的计算。对于第一问,需要根据长方体展开图的特征确定重合的点,再根据长方体表面积和体积公式进行计算;第二问根据平移的规律确定平移后点的坐标;第三问先画出圆,再分析重叠部分的形状并计算其面积。
答案:
(1) 把图形折成长方体后,点$F$、点$G$和点$H$重合。
由展开图可知长方体的长是$3$厘米、宽是$2$厘米、高是$1$厘米。
根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),可得表面积$S=(3×2 + 3×1 + 2×1)×2 = 22$(平方厘米)。
根据长方体体积公式$V = abh$,可得体积$V = 3×2×1 = 6$(立方厘米)。
(2) 数对的前一个数表示列,后一个数表示行。线段$CD$中$C$在第$2$列第$2$行,$D$在第$2$列第$1$行。
把线段$CD$向右平移$5$格,再向下平移$4$格,$D$原来在第$2$列第$1$行,向右平移$5$格后列变为$2 + 5 = 7$列,向下平移$4$格后行变为$1 - 4=-3$(这里行数用负数表示在原位置下方),但数对中一般不用负数表示行,从下往上数,原第$1$行向下平移$4$格后,相当于从新的最下面一行开始数,新的行数为$5 - 3 = 2$行(假设从下往上数最下面一行看作第$1$行),所以平移后点$D$的位置用数对表示是$(7,2)$。
(3) 图略。
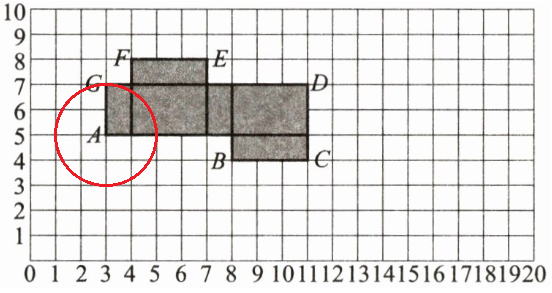
解析:本题主要考查长方体的展开图、平移、圆与长方体平面展开图重叠部分面积的计算。对于第一问,需要根据长方体展开图的特征确定重合的点,再根据长方体表面积和体积公式进行计算;第二问根据平移的规律确定平移后点的坐标;第三问先画出圆,再分析重叠部分的形状并计算其面积。
答案:
(1) 把图形折成长方体后,点$F$、点$G$和点$H$重合。
由展开图可知长方体的长是$3$厘米、宽是$2$厘米、高是$1$厘米。
根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),可得表面积$S=(3×2 + 3×1 + 2×1)×2 = 22$(平方厘米)。
根据长方体体积公式$V = abh$,可得体积$V = 3×2×1 = 6$(立方厘米)。
(2) 数对的前一个数表示列,后一个数表示行。线段$CD$中$C$在第$2$列第$2$行,$D$在第$2$列第$1$行。
把线段$CD$向右平移$5$格,再向下平移$4$格,$D$原来在第$2$列第$1$行,向右平移$5$格后列变为$2 + 5 = 7$列,向下平移$4$格后行变为$1 - 4=-3$(这里行数用负数表示在原位置下方),但数对中一般不用负数表示行,从下往上数,原第$1$行向下平移$4$格后,相当于从新的最下面一行开始数,新的行数为$5 - 3 = 2$行(假设从下往上数最下面一行看作第$1$行),所以平移后点$D$的位置用数对表示是$(7,2)$。
(3) 图略。

查看更多完整答案,请扫码查看


