《2025年新思维冲刺小升初达标总复习数学》

1. 某校六年级男生最喜欢的球类运动统计情况如图所示。
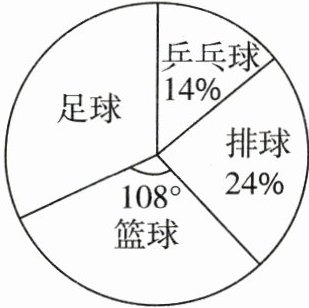
(1)最喜欢(乒乓球)的人数最少,最喜欢(足球)的人数最多。
(2)若最喜欢乒乓球的有35人,则六年级男生有(250)人,最喜欢排球的有(60)人。
(3)最喜欢篮球的占(30)%,最喜欢足球的占(32)%。

答案： 解析：本题主要考查了扇形统计图的知识点，通过扇形统计图中各部分所占比例来分析数据。
（1）从扇形统计图中可以直接看出各部分所占比例大小，比例最小的就是人数最少的球类运动，比例最大的就是人数最多的球类运动。
最喜欢乒乓球的占$14\%$，最喜欢排球的占$24\%$，最喜欢篮球的圆心角是$108^{\circ}$，因为整个圆是$360^{\circ}$，所以最喜欢篮球的占比为$\frac{108^{\circ}}{360^{\circ}} = 30\%$。
那么最喜欢足球的占比为$1 - 14\% - 24\% - 30\% = 32\%$。
比较$14\%$、$24\%$、$30\%$、$32\%$的大小，可得$14\% \lt 24\% \lt 30\% \lt 32\%$。
所以最喜欢乒乓球的人数最少，最喜欢足球的人数最多。
（2）已知最喜欢乒乓球的有$35$人，且最喜欢乒乓球的占$14\%$，根据“已知部分量和部分量占总量的百分比，求总量，用除法”，可得六年级男生总人数为$35÷14\% = 35÷0.14 = 250$（人）。
因为最喜欢排球的占$24\%$，所以最喜欢排球的人数为$250×24\% = 250×0.24 = 60$（人）。
（3）由前面计算可知，最喜欢篮球的占比为$30\%$，最喜欢足球的占比为$32\%$。
答案：
(1)乒乓球；足球。
(2)$250$；$60$。
(3)$30$；$32$。

2. 在括号里填“一定”或“可能”。
(1)有两个角是锐角的三角形(可能)是锐角三角形。
(2)有一个角是直角的平行四边形(一定)是长方形。
(3)有四个面相同的长方体(可能)是正方体。

答案： 解析：本题考查的是对三角形，平行四边形以及长方体的性质的理解以及“一定”和“可能”的运用。
(1)有两个角是锐角的三角形，并不意味着第三个角也一定是锐角，它也有可能是直角或钝角。
因此，这样的三角形可能是锐角三角形，也可能是直角三角形或钝角三角形。
所以，有两个角是锐角的三角形可能是锐角三角形。
(2)平行四边形的定义是两组对边平行。如果一个平行四边形有一个角是直角，那么它的对角也是直角（因为平行四边形的对角相等），从而它的另外两个角也必然是直角。
所以，有一个角是直角的平行四边形一定是长方形。
(3)长方体有六个面，每个面都是矩形。如果一个长方体有四个面相同，这并不意味着它的所有六个面都相同。
但是，如果长方体的四个侧面都是全等的矩形，并且顶面和底面也是与侧面全等的正方形（或矩形但与侧面尺寸相同），那么这个长方体就是一个正方体。
然而，只有四个面相同并不能保证其余两个面也与这四个面相同，除非这四个面是包括顶面和底面的。但题目只说有四个面相同，没有明确是哪四个面。
因此，有四个面相同的长方体可能是正方体，但也可能不是（例如，如果它的顶面和底面是正方形，但四个侧面是不同尺寸的矩形）。
所以，有四个面相同的长方体可能是正方体。
答案：
(1)可能，
(2)一定，
(3)可能。

3. 一个布袋里放有36支铅笔,其中红色铅笔25支,黄色铅笔10支,绿色铅笔1支。从布袋里任意摸1支,摸出(红)色铅笔的可能性最大。

答案： 解析：本题考查可能性的大小。
可能性的大小与物体的数量有关，物体数量越多，可能性越大。
红色铅笔有25支，黄色铅笔有10支，绿色铅笔有1支。
$25＞10＞1$，红色铅笔的数量最多。
所以摸出红色铅笔的可能性最大。
答案：红。

4. 52张扑克牌(除去大、小王)中有红桃、黑桃、方块、梅花4种花色的牌各13张。从中一次至少取出(5)张牌,才能保证有2张花色相同的牌。

答案： 解析：
题目考查的是抽屉原理（鸽巢原理）的应用。
我们需要找到至少取出多少张牌，才能保证有2张花色相同的牌。
最不利的情况是我们每次取出的都是不同花色的牌。
因为一共有4种花色，所以我们最开始可以连续取出4张都是不同花色的牌。
再取一张，就一定会有至少2张牌花色相同。
计算过程：
4（种花色，各取1张）+ 1（再取1张，确保有2张花色相同）= 5张
答案：
5

5. □□○○△△☆□□○○△△☆□□○○△△☆…按这样的排列规律,前40个图形中有(12)个□,第40个图形是(△)。

答案： 该图形序列按“□□○○△△☆”7个图形为一组循环排列。
40÷7=5（组）……5（个），即有5组完整循环，余5个图形。
每组有2个□，5组共有2×5=10个□，余下的5个图形中有2个□，所以前40个图形中□的总数为10+2=12个。
余下5个图形依次为□□○○△，第5个是△，故第40个图形是△。
12；△