《2025年新思维冲刺小升初达标总复习数学》

5. 从里面量一个长方体容器,长5分米,宽4分米,高10分米。里面已经竖直放了一个长4分米、宽2分米、高7分米的长方体铁块。如果再把124升水倒入容器中,那么水深多少分米?

答案： 解析：本题考查长方体体积的计算。
首先需要明确，当水被倒入容器时，它会先填满铁块周围的空隙，然后再上升。
根据长方体的体积公式：
体积 $=$ 长$×$ 宽$×$ 高
容器的底面积是 $5× 4=20$（平方分米）。
铁块的底面积是 $4× 2=8$（平方分米）。
所以，水可以填充的底面积是容器底面积减去铁块底面积，即：
$20-8=12$（平方分米）
当124升水（即124立方分米）被倒入时，它会占据一定的水深。这个水深可以通过水的体积除以水可以填充的底面积来计算，即：
$124÷12=\frac{31}{3}$（分米）
但是，需要考虑到铁块的高度。因为铁块的高度是7分米，所以水深不能超过铁块的高度。
而$\frac{31}{3}$分米$＞7$分米，
说明水会淹没铁块，并且继续上升，
此时，把铁块的高度7分米代入：
$124-12×7=40$（立方分米）
$40÷(5×4)=2$（分米）
$7+2=9$（分米）
所以，倒入124升水后，总的水深是9分米。
答案：9分米。

6. 工人用薄木板钉成一个长方体包装箱,并用尼龙编织条(如图)在三个方向上加固,所用尼龙编织条的长度分别为365厘米、405厘米、485厘米。若每个尼龙编织条接头处的重叠部分都是5厘米,则这个长方体包装箱的体积是多少立方米?

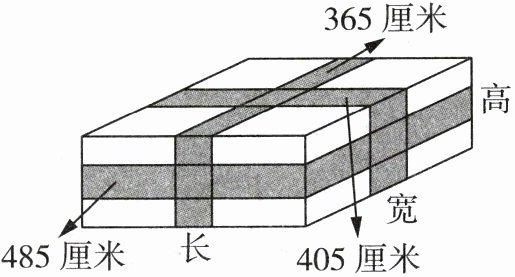
答案： 365-5=360(厘米)
405-5=400(厘米)
485-5=480(厘米)
360+400+480=1240(厘米)
1240÷4=310(厘米)
长：310-(360÷2)=130(厘米)
宽：310-(400÷2)=110(厘米)
高：310-(480÷2)=70(厘米)
130×110×70=1001000(立方厘米)
1001000立方厘米=1.001立方米
答：这个长方体包装箱的体积是1.001立方米。

7. 有大、中、小三个底面是正方形的长方体水池,它们的底面边长分别是6米、3米、2米。把两堆碎石分别浸没在中、小水池的水里,两个水池的水面分别升高了6厘米和9厘米。如果将这两堆碎石都浸没在大水池的水里,那么大水池的水面会升高多少厘米? (水均未溢出)

答案： 解析：
本题考查长方体体积的计算。
中水池的底面边长是3米，水面升高了6厘米（0.06米），
所以中水池内碎石的体积是：
$V_{\text{中}} = 3 × 3 × 0.06 = 0.54 \text{(立方米)}$
小水池的底面边长是2米，水面升高了9厘米（0.09米），
所以小水池内碎石的体积是：
$V_{\text{小}} = 2 × 2 × 0.09 = 0.36 \text{(立方米)}$
所以两堆碎石的总体积是：
$V_{\text{总}} = V_{\text{中}} + V_{\text{小}} = 0.54 + 0.36 = 0.9 \text{(立方米)}$
大水池的底面边长是6米，设水面升高的高度为$h$米，
则大水池内水面升高的体积应等于两堆碎石的总体积，
即：$6 × 6 × h = 0.9$
解得$h = \frac{0.9}{36} = 0.025 \text{米}$
将高度转换为厘米，
即 $0.025 \text{米} = 2.5 \text{厘米}$
答案：
大水池的水面会升高2.5厘米。