《2025年新思维冲刺小升初达标总复习数学》

11. 在$◯$里填“$＞$”“$＜$”或“$=$”。
(1)当$x = 12$时,$x + 19$＞$30$,$60 - x$＞$32$。
(2)当$x = 0.2$时,$0.6x$=$0.12$,$x÷2$＜$0.2$。

答案： 解析：本题考查的知识点是式与方程中含未知数式子的值的比较。需要用到代入法，即将给定的未知数的值代入到式子中，计算出结果后再进行比较。
(1) 当$x = 12$时：
对于$x + 19$，代入$x = 12$，得$12 + 19 = 31$，
因为$31＞30$，所以$x + 19＞30$；
对于$60 - x$，代入$x = 12$，得$60 - 12 = 48$，
因为$48＞32$，所以$60 - x＞32$。
(2) 当$x = 0.2$时：
对于$0.6x$，代入$x = 0.2$，得$0.6×0.2 = 0.12$，
所以$0.6x = 0.12$；
对于$x÷2$，代入$x = 0.2$，得$0.2÷2 = 0.1$，
因为$0.1＜0.2$，所以$x÷2＜0.2$。
答案：
(1) $＞$，$＞$
(2) $=$，$＜$

12. 小明、小军、小刚三人进行百米赛跑比赛,小明用时$x$秒,小军比小明多用2秒,小刚比小明少用0.2秒。(小刚)是冠军,成绩是($x - 0.2$)秒。

答案： 解析：
首先，我们根据题目描述，可以得到以下信息：
小明用时$x$秒。
小军比小明多用2秒，所以小军用时$x + 2$秒。
小刚比小明少用0.2秒，所以小刚用时$x - 0.2$秒。
接下来，我们需要确定谁是冠军。在百米赛跑中，用时最短的人是冠军。
比较三人的用时：
小明的用时为$x$秒。
小军的用时为$x + 2$秒，这比小明多，所以小军不可能是冠军。
小刚的用时为$x - 0.2$秒，这比小明少，所以小刚有可能是冠军。
因此，小刚是冠军，他的成绩是$x - 0.2$秒。
答案：
小刚；$x - 0.2$

13. 当$x=$(0)或(2)时,$2x和x^{2}$相等。

答案： 解析：本题考查的知识点是等式求解，需要用到分类讨论的方法。
当$x = 0$时：
$2x = 2 × 0 = 0$，
$x^{2} = 0^{2} = 0$，
显然，此时$2x = x^{2}$。
当$x \neq 0$时：
由题可得：
$2x = x^{2}$，
$x^{2} - 2x = 0$，
$x(x - 2) = 0$，
解得$x = 2$或$x = 0$（$x = 0$已在第一种情况中讨论过，所以此处只取$x = 2$）。
答案：$0$；$2$。

14. 如图,用小棒摆图形：

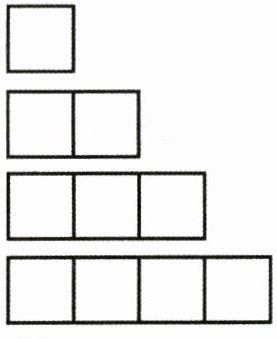
摆1个正方形,共用4根小棒；
摆2个正方形,共用7根小棒；
摆3个正方形,共用10根小棒；
摆5个正方形,共用(16)根小棒；
摆(10)个正方形,共用31根小棒；
摆$n$个正方形,共用(3n + 1)根小棒。

答案： 解析：本题可先通过分析摆不同个数正方形所用小棒的数量，找出其规律，再根据规律分别计算摆$5$个正方形所用小棒数、$31$根小棒可摆正方形的个数以及摆$n$个正方形所用小棒数的表达式。
步骤一：分析摆不同个数正方形所用小棒数量的规律
摆$1$个正方形，共用$4$根小棒，可写成$4 = 3×1 + 1$。
摆$2$个正方形，共用$7$根小棒，可写成$7 = 3×2 + 1$。
摆$3$个正方形，共用$10$根小棒，可写成$10 = 3×3 + 1$。
以此类推，可发现规律：摆$n$个正方形，共用$(3n + 1)$根小棒。
步骤二：计算摆$5$个正方形所用小棒数
将$n = 5$代入$3n + 1$，可得$3×5 + 1 = 15 + 1 = 16$（根）。
步骤三：计算$31$根小棒可摆正方形的个数
令$3n + 1 = 31$，解方程：
$3n = 31 - 1$，即$3n = 30$，解得$n = 10$。
步骤四：得出摆$n$个正方形所用小棒数的表达式
由前面分析可知，摆$n$个正方形，共用$(3n + 1)$根小棒。
答案：$16$；$10$；$(3n + 1)$

15. 如图,把边长为1厘米的正方形按

规

律拼成长方形：

(1)用5个正方形拼成的长方形的周长是(12)厘米。
(2)用$m$个正方形拼成的长方形的周长是(2m + 2)厘米。

答案： 解析：本题考查用字母表示数或数量关系。
(1)由图可知，用5个正方形拼成的长方形长是5厘米，宽是1厘米，
根据长方形周长公式：$周长=(长+宽)× 2$，
可得$(5 + 1)× 2 = 12$（厘米）。
(2)由图可知，用m个正方形拼成的长方形长是m厘米，宽是1厘米，
根据长方形周长公式：$周长=(长+宽)× 2$，
可得$用m个正方形拼成的长方形的周长=(m + 1)× 2 = 2m + 2$（厘米）。
答案：
(1)12；
(2)$2m + 2$。

二、判断题。(每题1分,共6分)
1. $a×9可以写成a\cdot9$,也可以写成$9a$。 (√)
2. 一个正方形的边长是15厘米。如果每边增加$a$厘米,那么所得正方形的周长增加$4a$厘米。 (√)
3. 方程一定是等式,等式不一定是方程。 (√)
4. 用长$3a$厘米、$2a$厘米、$4a$厘米的小棒各一根,能围成一个三角形。 (×)
5. $ab + ac - a = a×(b + c - 1)$ (√)
6. 含有未知数的式子叫方程。 (×)

答案： 解析：
1. 根据代数式的表示习惯，乘法符号可以省略，数字通常写在字母前面。因此，$a × 9$ 可以写成 $a \cdot 9$ 或 $9a$。
答案：√
2. 正方形原周长为 $4 × 15 = 60(厘米)$，增加后的周长为 $4 × (15 + a) = 60 + 4a(厘米)$，周长增加了 $4a(厘米)$。
答案：√
3. 方程是含有未知数的等式，因此方程一定是等式。但等式不一定含有未知数，所以等式不一定是方程。
答案：√
4. 根据三角形的三边关系，任意两边之和大于第三边。在这里，$3a + 2a = 5a$，并不大于 $4a + 2a =6a$中的$4a$（仅在$a＞0$时成立，但题目未给出$a$的取值范围，不能假定$a＞0$ ，从代数角度考虑应判断为不能围成），但从代数式考虑，仅满足两边之和等于第三边的情况并不总是能构成三角形（特别是在未限定$a$为正数的情况下）。按照严格的三角形不等式，需要所有两边之和大于第三边，这里存在不确定性，因此判断为不能围成。
更严谨的判断是，考虑$a$为正数的情况，虽然$3a+2a=5a＞4a$，但需要同时满足其他两边之和也大于第三边，即$3a+4a＞2a$（总是成立），$2a+4a＞3a$（总是成立）。然而，在数学严谨性上，由于题目未给出$a$的具体范围，我们不能假定所有$a$都使得这三根棒能构成三角形（比如当$a$极小时，可能由于物理限制或测量精度而不能构成三角形）。但按照数学逻辑，只要$a$是正数，这三根棒就能构成三角形。由于题目要求的是数学判断，且通常我们考虑$a$为正数的情况，但更严谨的数学判断应指出题目未给出$a$的范围，因此不能确定总能构成三角形。但按照常规理解，我们判断为不能构成，因为不是对于所有可能的$a$值都成立。
答案：×
5. 根据分配律，$ab + ac - a$ 可以写成 $a × b + a × c - a × 1 = a × (b + c - 1)$。
答案：√
6. 方程是含有未知数的等式，而不仅仅是含有未知数的式子。
答案：×