《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

10. 如图所示的平行六面体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$AD = AA_{1}=AB = 1$，$\angle A_{1}AB=\angle DAB=\angle DAA_{1}=60^{\circ}$，$\overrightarrow{A_{1}C_{1}} = 3\overrightarrow{NC_{1}}$，$\overrightarrow{D_{1}B}=2\overrightarrow{MB}$，设$\overrightarrow{AB}=\boldsymbol{a}$，$\overrightarrow{AD}=\boldsymbol{b}$，$\overrightarrow{AA_{1}}=\boldsymbol{c}$.
(1)试用$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$表示$\overrightarrow{MN}$；
(2)求$MN$的长度.

答案： 10.解　
(1)MN=MD+DA+AN=−$\frac{1}{2}$DB−
AD+$\frac{2}{3}$AC=−$\frac{1}{2}$(DD+DB)−AD+$\frac{2}{3}$(AB+
AD)=−$\frac{1}{2}$D,D−$\frac{1}{2}$(DA+DC)−AD+$\frac{2}{3}$(AB+
AD)=$\frac{1}{2}$C−$\frac{1}{2}$(a−b)−b+$\frac{2}{3}$(a+b)=$\frac{1}{6}$a+$\frac{1}{6}$b+$\frac{1}{2}$C.
(2)由
(1)知MN=$\frac{1}{6}$a+$\frac{1}{6}$b+立,
　又AD=AA:=AB=1,
　∠AAB=∠DAB=∠DAA1=60°,
∴a.b=a.c=b.c=1×1×$\frac{1}{2}$=$\frac{1}{2}$,
∴|MN|=　$\sqrt{\frac{1}{6}a+\frac{1}{6}b+\frac{1}{2}}$
　=　$\sqrt{\frac{1}{36}a²+\frac{1}{36}b²+\frac{1}{4}c²+\frac{1}{18}a.b+\frac{1}{6}a.c+\frac{1}{6}b−c}$
　=$\frac{√2}{2}$
∴MN的长度为$\frac{\sqrt{2}}{2}$.

11. 已知空间四边形$OABC$中，$M$在$AO$上，满足$\frac{AM}{MO}=\frac{1}{2}$，$N$是$BC$的中点，且$\overrightarrow{AO}=\boldsymbol{a}$，$\overrightarrow{AB}=\boldsymbol{b}$，$\overrightarrow{AC}=\boldsymbol{c}$，用$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$表示向量$\overrightarrow{MN}$为（ ）
A. $\frac{1}{3}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$
B. $\frac{1}{3}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}-\frac{1}{2}\boldsymbol{c}$
C. $-\frac{1}{3}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$
D. $\frac{1}{3}\boldsymbol{a}-\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$

答案： 11.C　MN=MA+AB+BN=MA+AB+$\frac{1}{2}$BC=
　MA+AB+$\frac{1}{2}$(AC−AB)=MA+$\frac{1}{2}$AB+$\frac{1}{2}$AC=
　−$\frac{1}{3}$a+$\frac{1}{2}$b+$\frac{1}{2}$c.故选C.

12. 已知棱长均为$3$的三棱锥$S - ABC$，若空间一点$P$满足$\overrightarrow{SP}=x\overrightarrow{SA}+y\overrightarrow{SB}+z\overrightarrow{SC}(x + y + z = 1)$，则$|\overrightarrow{SP}|$的最小值为（ ）
A. $\sqrt{6}$
B. $\frac{\sqrt{6}}{3}$
C. $\frac{\sqrt{3}}{6}$
D. $1$

答案：
12.A　由SP=xSA+ySB+NSC
　(x+y+x=1)及空间向量基本定
　理知,P与A,B,C共面,则|SP|的
　　　　　　　　　　　　 最小值为三棱锥的高.设O为S在
　平面ABC上的射影，由条件可得三
　棱锥S−ABC为正三棱锥.连接CO并延长交AB于点H,如图所示,则H为AB中点，且CH⊥AB,所以
CH=$\frac{3\sqrt{3}}{2}$,CO=$\sqrt{3}$,所以SO=$\sqrt{3²−(\sqrt{3})²}$=$\sqrt{6}$,则|SP|的最小值为$\sqrt{6}$.故选A.

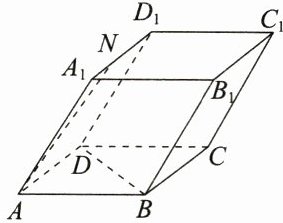
13. （2023·广东佛山质检）在如图所示的平行六面体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，已知$AB = AA_{1}=AD$，$\angle BAD=\angle DAA_{1}=60^{\circ}$，$\angle BAA_{1}=30^{\circ}$，$N$为$A_{1}D_{1}$上一点，且$A_{1}N=\lambda A_{1}D_{1}$. 若$BD\perp AN$，则$\lambda$的值为________.

答案： 13.$\sqrt{3}$−1
　解析　设AB=a,AD=b,AA=c,则BD=AD−
AB=b−a.
　因为AN=λA1D,所以AN=AA+AN=c+λb.若BD⊥AN,则BD⊥AN,所以BD.AN=(b−a).(c+λb)=0.不妨取AB=AA=AD=1,则a.b=1×1×cos60°=$\frac{1}{2}$,b.c=1×1×cos60°=$\frac{1}{2}$,a.c=1×1×cos30°=$\frac{\sqrt{3}}{2}$,所以(b−a).(c+λb)=b.c+λb²−a.c−λa.b=$\frac{1}{2}$+λ−$\frac{\sqrt{3}}{2}$−$\frac{1}{2}$=0,解得λ=$\sqrt{3}$−1.

14. 如图，在三棱锥$P - ABC$中，点$G$为$\triangle ABC$的重心，点$M$在$PG$上，且$PM = 3MG$，过点$M$任意作一个平面分别交线段$PA$，$PB$，$PC$于点$D$，$E$，$F$，若$\overrightarrow{PD}=m\overrightarrow{PA}$，$\overrightarrow{PE}=n\overrightarrow{PB}$，$\overrightarrow{PF}=t\overrightarrow{PC}$，求证$\frac{1}{m}+\frac{1}{n}+\frac{1}{t}$为定值，并求出该定值.

答案：
14.解　如图,连接AG并延长交BC于点
　H,由题意,可令{PA,PB,PC}为空间
　的一个基底，
　　　　　　　　　　　　　 PM=$\frac{3}{4}$PG=$\frac{3}{4}$(PA+AG)=
　$\frac{3}{4}$PA+$\frac{3}{4}$×$\frac{2}{3}$AH=$\frac{3}{4}$PA+$\frac{1}{2}$×$\frac{1}{2}$(AB+AC)=
　$\frac{3}{4}$PA+$\frac{1}{4}$(PB−PA)+$\frac{1}{4}$(PC−PA)=$\frac{1}{4}$PA+$\frac{1}{4}$PB+$\frac{1}{4}$PC.
　连使接得DDMM=,因D为E点+Dμ$\frac{,E.}{DF}$,F即,MPM共−$\frac{.}{PD}$=以λ存(P在E实−数PDλ,)μ+,μ(PF−PD),
　所以PM=(1−λ−μ)PD+aPE+μPF=(1−λ−μ)mPA+AnPB+PC.
　由空间向量基本定理，知$\frac{1}{4}$=(1−λ−μ)m,$\frac{1}{4}$=λn,$\frac{1}{4}$=t,所以$\frac{1}{m}$+$\frac{1}{n}$+$\frac{1}{t}$=4(1−λ−μ)+4λ+4=4,为定值.

15. （数学抽象）（2024·辽宁沈阳期末）已知$\boldsymbol{e}_{1}$，$\boldsymbol{e}_{2}$是空间单位向量，$\boldsymbol{e}_{1}\cdot\boldsymbol{e}_{2}=\frac{1}{2}$. 若空间向量$\boldsymbol{b}$满足$\boldsymbol{b}\cdot\boldsymbol{e}_{1}=2$，$\boldsymbol{b}\cdot\boldsymbol{e}_{2}=\frac{5}{2}$，且对于任意$x$，$y\in\mathbf{R}$，$|\boldsymbol{b}-(x\boldsymbol{e}_{1}+y\boldsymbol{e}_{2})|\geqslant|\boldsymbol{b}-(x_{0}\boldsymbol{e}_{1}+y_{0}\boldsymbol{e}_{2})| = 1(x_{0},y_{0}\in\mathbf{R})$，则$x_{0}=$________，$y_{0}=$________，$|\boldsymbol{b}|=$________.

答案： 15.122$\sqrt{2}$
　解析　由题意可令b=xe+y。e2+e3,其中|e3|=1,且e3⊥e,i=1,2.由b.e=2得x。+$\frac{y.}{2}$=2,由b.e2=$\frac{5}{2}$得$\frac{x}{2}$+y。=$\frac{5}{2}$,解得x。=1,y。=2,
∴|b{=
　　$\sqrt{(e+2e+e)²}$=2$\sqrt{2}$