《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

11. 已知$MN$是棱长为 2 的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$内切球的一条直径，则$\overrightarrow{AM}\cdot\overrightarrow{AN}=$（ ）
A. $-1$
B. 1
C. $-2$
D. 2

答案： 11.D因为正方体ABCD−AlBlClD的棱长为2,故其内切球的半径r=$\frac{1}{2}$×2=1.又球心一定在体对角线的中点处，且体对角线长为　$\sqrt{2²+2²+2²}$=2$\sqrt{3}$,不妨设内切球的球心为O,则AO=$\sqrt{3}$,OM=ON=1,AM=A0+OM,AN=AO+ON,则AM.AN=(AO+OM).(AO+ON)=|Aδ|²+A0.(OM+ON)+OM.ON=3+0−1=2.故选D.

12.（多选）在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，下列结论正确的是（ ）
A. 四边形$ABC_{1}D_{1}$的面积为$|\overrightarrow{AB}||\overrightarrow{BC_{1}}|$
B. $\overrightarrow{AD_{1}}$与$\overrightarrow{A_{1}B}$的夹角为$60^{\circ}$
C. $(\overrightarrow{AA_{1}}+\overrightarrow{A_{1}D_{1}}+\overrightarrow{A_{1}B_{1}})^{2}=3\overrightarrow{A_{1}B_{1}}^{2}$
D. $\overrightarrow{A_{1}C}\cdot(\overrightarrow{A_{1}B_{1}}-\overrightarrow{A_{1}D_{1}})=0$

答案： 12.ACD　由AB⊥平面BBClC得AB⊥BC1,
∴四边形
ABCD，的面积为|AB|BC1,故A正确;
∵△ACD1 是等边三角形,
∴∠ADC=60°,又
∵AB//D;C,
∴异面直线AD与AB的夹角为60°,但是向量AD与
AB的夹角为120°,故B错误;由向量加法的运算法则可以得到AA+AD+AB=AC,
∵AC²=3AB²,
∴(AA+AD+AB)²=3AB²,故C正确;由向量运算可得AB−AD=DB,
∵在正方体
ABCD−ABCD中,DB⊥平面AAClC,AlCC平面AAC,C,
∴DB1⊥AC,
∴AC.DB=O,故D 正确.故选ACD.

13. 如图，已知四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$的底面$ABCD$是矩形，$AB = 4$，$AA_{1} = 3$，$AD = 2$，$\angle BAA_{1} = \angle DAA_{1} = 60^{\circ}$，$E$为棱$C_{1}D_{1}$的中点，则$|\overrightarrow{AE}| =$________，$\overrightarrow{AE}$在$\overrightarrow{AB}$上的投影向量是________.

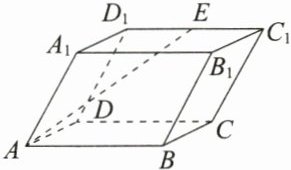
答案： 13.$\sqrt{29}$$\frac{7}{8}$AB
　解析　由题图可知AE=AA+AD+DE=AA+
AD+$\frac{1}{2}$AB,所以|AE1²=|AA+AD+$\frac{1}{2}$AB|2=
　|AA;1²+|AD|²+$\frac{1}{4}$1AB|²+2AA.AD+AA.
AB+AD.AB=3²+2²+$\frac{1}{4}$×4²+2×3×2×$\frac{1}{2}$+3×4×$\frac{1}{2}$+0=29,所以|AE|=$\sqrt{29}$二
AB.AE=AB.(AA+AD+$\frac{1}{2}$AB)=AB.AA+
AB.AD+$\frac{1}{2}$AB2=4×3×$\frac{1}{2}$+0+$\frac{1}{2}$×4²=14,所以AE在AB上的投影向量是AB.AE　AB |AB|　.AB=
　$\frac{7}{8}$AB.

14. 如图，在空间四边形$OABC$中，$E$是线段$BC$的中点，$G$在线段$AE$上，且$AG = 2GE$.
(1)试用$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$；
(2)若$OA = 2$，$OB = 3$，$OC = 4$，$\angle AOC = \angle BOC = 60^{\circ}$，$\angle AOB = 90^{\circ}$，求$\overrightarrow{OG}\cdot\overrightarrow{AB}$的值及$|\overrightarrow{OG}|$.

答案： 14.解　
(1)OG=OA+AG=ōA+$\frac{2}{3}$AE=OA+$\frac{2}{3}$(ōE−ōA)=$\frac{1}{3}$A+$\frac{2}{3}$ōE=$\frac{1}{3}$ōA+$\frac{2}{3}$
　$\frac{1}{2}$(OB+OC)=$\frac{1}{3}$OA+OB+OC.
(2)0G.AB=$\frac{1}{3}$(OA+ōB+OC).(OB−OA)=
　$\frac{1}{3}$(OB−ōA²+OC.OB−0C.OA)=$\frac{1}{3}$(3²−2²+4×3cos60°−4×2cos60°)=$\frac{7}{3}$
　āG}=$\frac{1}{3}$$\sqrt{(OA+OB+OC)2}$
　=$\frac{1}{3}$√0A²+OB+0C+20A.OB+2āB.0C+20A.0 =$\frac{1}{3}$$\sqrt{2²+3²+4²+0+2×3×4cos60°+2×2×4cos60°}$
　=$\frac{7}{3}$.

15.（逻辑推理）（2023·广东深圳红岭中学期中）已知空间向量$\boldsymbol{a}$，$\boldsymbol{b}$满足$|\boldsymbol{a}| = |\boldsymbol{b}| = 1$，且$\boldsymbol{a}$，$\boldsymbol{b}$的夹角为$\frac{\pi}{3}$，点$O$，$A$，$B$满足$\overrightarrow{OA}=2\boldsymbol{a}+\boldsymbol{b}$，$\overrightarrow{OB}=3\boldsymbol{a}-\boldsymbol{b}$，则$\triangle OAB$的面积为（ ）
A. $\frac{5\sqrt{3}}{2}$
B. $\frac{5\sqrt{3}}{4}$
C. $\frac{7\sqrt{3}}{4}$
D. $\frac{11}{4}$

答案： 15.B由题意得|OA|=$\sqrt{(2a+b)²}$=$\sqrt{4a²+b²+4a.b}$=
　　$\sqrt{4+1+4×1×1×\frac{1}{2}}$=√,1OB1=　$\sqrt{(3a−b)}$=
　　$\sqrt{9a²−6a.b+b²}$=$\sqrt{9−6×1×1ײ+1=}$　　$\sqrt{7}$,则cos＜OA,OB)=|OAA|.OOBB=$\frac{6a²−b²+a.b}{7}$=$\frac{11}{14}$,所以sin∠AOB=　　　　$\sqrt{1−(\frac{11}{14}}$=$\frac{5\sqrt{3}}{14}$,所以△OAB的面积S=$\frac{1}{2}$OA|.|OB|sin∠AOB=$\frac{1}{2}$×$\sqrt{7}$×√×$\frac{5\sqrt{3}}{14}$=
　$\frac{5\sqrt{3}}{4}$,故选B.

16.（直观想象）已知正四面体$A - BCD$的外接球半径为 3，$MN$为其外接球的一条直径，$P$为正四面体$A - BCD$表面上任意一点，则$\overrightarrow{PM}\cdot\overrightarrow{PN}$的最小值为________.

答案： 16.−8
　解析　设正四面体A−BCD的外接球、内切球的球心均为O,内切球半径为r，正四面体的高为h,一个面的面积为S,则VA|BCD=4×$\frac{1}{3}$Sr=$\frac{1}{3}$Sh,所以h=4r.
　又正四面体A−BCD的外接球半径为3,显然r+3=
　h=4r,所以r=1,即|PO|mn=1.
　O所M以.POMN.=PPNO=2−(P9≥O1+−O9M=)−.8(.P故OP+MO忒.$\frac{)=}{PN}$)=P的O最²+小值为−8.