2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10.(1)设坐标平面内三点A(m,-m - 3),B(2,m - 1),C(-1,4),若直线AC的斜率是直线BC的斜率的3倍,求实数m的值;
(2)已知直线$l_1$的斜率为$\frac{1}{2}$,直线$l_2$的倾斜角是直线$l_1$倾斜角的2倍,求直线$l_2$的斜率.
(2)已知直线$l_1$的斜率为$\frac{1}{2}$,直线$l_2$的倾斜角是直线$l_1$倾斜角的2倍,求直线$l_2$的斜率.
答案:
解
(1) 由 $k_{AC}=3k_{BC}$,得 $\frac{4-(-m - 3)}{-1 - m}=3\cdot\frac{4-(m - 1)}{-1 - 2}$,解得 $m = 1$ 或 $m = 2$,
经检验均符合题意,故 $m$ 的值是 $1$ 或 $2$.
(2) 设直线 $l_{1}$ 的倾斜角为 $\alpha$,则直线 $l_{2}$ 的倾斜角为 $2\alpha$.
由已知,$\tan\alpha=\frac{1}{2}$,得直线 $l_{2}$ 的斜率为 $\tan2\alpha=\frac{2\tan\alpha}{1-\tan^{2}\alpha}=\frac{4}{3}$.
(1) 由 $k_{AC}=3k_{BC}$,得 $\frac{4-(-m - 3)}{-1 - m}=3\cdot\frac{4-(m - 1)}{-1 - 2}$,解得 $m = 1$ 或 $m = 2$,
经检验均符合题意,故 $m$ 的值是 $1$ 或 $2$.
(2) 设直线 $l_{1}$ 的倾斜角为 $\alpha$,则直线 $l_{2}$ 的倾斜角为 $2\alpha$.
由已知,$\tan\alpha=\frac{1}{2}$,得直线 $l_{2}$ 的斜率为 $\tan2\alpha=\frac{2\tan\alpha}{1-\tan^{2}\alpha}=\frac{4}{3}$.
11.(多选)已知三条直线$l_1$,$l_2$,$l_3$的斜率分别为$k_1$,$k_2$,$k_3$,倾斜角分别为$\alpha$,$\beta$,$\gamma$. 若$\alpha < \beta < \gamma$,则下列关系可能成立的是 ( )
A. $k_3 < k_1 < k_2$
B. $k_1 < k_2 < k_3$
C. $k_2 < k_3 < k_1$
D. $k_3 < k_2 < k_1$
A. $k_3 < k_1 < k_2$
B. $k_1 < k_2 < k_3$
C. $k_2 < k_3 < k_1$
D. $k_3 < k_2 < k_1$
答案:
ABC 根据直线的斜率与倾斜角的关系有:当 $0\leqslant\alpha\lt\beta\lt\gamma\lt\frac{\pi}{2}$ 或 $\frac{\pi}{2}\lt\alpha\lt\beta\lt\gamma\lt\pi$ 时,$0\leqslant k_{1}\lt k_{2}\lt k_{3}$ 或 $k_{1}\lt k_{2}\lt k_{3}\lt0$,故选项 B 可能成立;当 $0\leqslant\alpha\lt\beta\lt\frac{\pi}{2}\lt\gamma\lt\pi$ 时,$k_{3}\lt0\leqslant k_{1}\lt k_{2}$,故选项 A 可能成立;当 $0\leqslant\alpha\lt\frac{\pi}{2}\lt\beta\lt\gamma\lt\pi$ 时,$k_{2}\lt k_{3}\lt0\leqslant k_{1}$,故选项 C 可能成立;选项 D 不可能成立. 故选 ABC.
12. 设A(2,-3),B(-3,-2),直线l过点P(1,2)且与线段AB相交,则l的斜率k存在时,k的取值范围是 ( )
A. $k\leq -1$或$k\geq 5$
B. $-5\leq k\leq 1$
C. $-1\leq k\leq 5$
D. $k\leq -5$或$k\geq 1$
A. $k\leq -1$或$k\geq 5$
B. $-5\leq k\leq 1$
C. $-1\leq k\leq 5$
D. $k\leq -5$或$k\geq 1$
答案:
D 由题意可得 $k_{PA}=\frac{2-(-3)}{1 - 2}=-5$,$k_{PB}=\frac{-2 - 2}{-3 - 1}=1$,因为直线 $l$ 与线段 $AB$ 相交,所以 $k\geqslant1$ 或 $k\leqslant - 5$,故选 D.
13.(2024·江西南昌质检)已知直线l的倾斜角为$\alpha$,斜率为k,若$k\in[-\sqrt{3},1]$,则$\alpha$的取值范围为______________.
答案:
$\left\{\alpha\mid0\leqslant\alpha\leqslant\frac{\pi}{4}或\frac{2\pi}{3}\leqslant\alpha\lt\pi\right\}$
解析 斜率 $k = \tan\alpha$,且 $\alpha\in[0,\pi)$,当 $k\in[0,1]$ 时,即 $0\leqslant\tan\alpha\leqslant1$,解得 $0\leqslant\alpha\leqslant\frac{\pi}{4}$,当 $k\in[-\sqrt{3},0)$ 时,即 $-\sqrt{3}\leqslant\tan\alpha\lt0$,解得 $\frac{2\pi}{3}\leqslant\alpha\lt\pi$,所以 $\alpha$ 的取值范围为 $\left\{\alpha\mid0\leqslant\alpha\leqslant\frac{\pi}{4}或\frac{2\pi}{3}\leqslant\alpha\lt\pi\right\}$.
解析 斜率 $k = \tan\alpha$,且 $\alpha\in[0,\pi)$,当 $k\in[0,1]$ 时,即 $0\leqslant\tan\alpha\leqslant1$,解得 $0\leqslant\alpha\leqslant\frac{\pi}{4}$,当 $k\in[-\sqrt{3},0)$ 时,即 $-\sqrt{3}\leqslant\tan\alpha\lt0$,解得 $\frac{2\pi}{3}\leqslant\alpha\lt\pi$,所以 $\alpha$ 的取值范围为 $\left\{\alpha\mid0\leqslant\alpha\leqslant\frac{\pi}{4}或\frac{2\pi}{3}\leqslant\alpha\lt\pi\right\}$.
14. 已知A(3,1),B(2,4),C(m,2)三点.
(1)若直线BC的倾斜角为135°,求m的值;
(2)是否存在m,使得A,B,C三点共线?若存在,求m的值;若不存在,说明理由.
(1)若直线BC的倾斜角为135°,求m的值;
(2)是否存在m,使得A,B,C三点共线?若存在,求m的值;若不存在,说明理由.
答案:
解
(1) 因为 $B(2,4)$,$C(m,2)$,直线 $BC$ 的倾斜角为 $135^{\circ}$,
所以 $k_{BC}=\tan135^{\circ}=-1=\frac{4 - 2}{2 - m}$,解得 $m = 4$,
故 $m$ 的值为 $4$.
(2) 当 $A$,$B$,$C$ 三点共线时,$k_{AB}=k_{BC}$,即 $\frac{4 - 1}{2 - 3}=\frac{4 - 2}{2 - m}$,
解得 $m=\frac{8}{3}$,
所以存在 $m$,使得 $A$,$B$,$C$ 三点共线,此时 $m=\frac{8}{3}$.
(1) 因为 $B(2,4)$,$C(m,2)$,直线 $BC$ 的倾斜角为 $135^{\circ}$,
所以 $k_{BC}=\tan135^{\circ}=-1=\frac{4 - 2}{2 - m}$,解得 $m = 4$,
故 $m$ 的值为 $4$.
(2) 当 $A$,$B$,$C$ 三点共线时,$k_{AB}=k_{BC}$,即 $\frac{4 - 1}{2 - 3}=\frac{4 - 2}{2 - m}$,
解得 $m=\frac{8}{3}$,
所以存在 $m$,使得 $A$,$B$,$C$ 三点共线,此时 $m=\frac{8}{3}$.
15.(直观想象)斜拉桥是桥梁建筑的一种形式,在桥梁平面上有多根拉索,所有拉索的合力方向与中央索塔一致. 如图,一座斜拉桥共有10对永久拉索,在索塔两侧对称排列. 已知拉索上端相邻两个锚的间距$\vert P_iP_{i + 1}\vert(i = 1,2,3,\cdots,9)$均为4.4 m,拉索下端相邻两个锚的间距$\vert A_iA_{i + 1}\vert(i = 1,2,3,\cdots,9)$均为16 m. 最短拉索的两个锚$P_1$,$A_1$满足$\vert OP_1\vert = 57$ m,$\vert OA_1\vert = 86$ m,则最长拉索所在直线的斜率为 ( )

A. $\pm 0.40$
B. $\pm 0.42$
C. $\pm 0.43$
D. $\pm 0.45$

A. $\pm 0.40$
B. $\pm 0.42$
C. $\pm 0.43$
D. $\pm 0.45$
答案:
B 如图,以 $O$ 为原点建系,
因为最短拉索的两个锚 $P_{1}$,$A_{1}$ 满足 $|OP_{1}| = 57\ m$,$|OA_{1}| = 86\ m$,
且拉索上端相邻两个锚的间距 $|P_{i}P_{i + 1}|(i = 1,2,3,\cdots,9)$ 均为 $4.4\ m$,拉索下端相邻两个锚的间距 $|A_{i}A_{i + 1}|(i = 1,2,3,\cdots,9)$ 均为 $16\ m$,
则 $|OA_{10}| = |OA_{1}|+|A_{1}A_{10}| = 86 + 9\times16 = 230\ m$,即点 $A_{10}(230,0)$,同理 $B_{10}(-230,0)$,
又 $|OP_{10}| = |OP_{1}|+|P_{1}P_{10}| = 57 + 9\times4.4 = 96.6\ m$,即点 $P_{10}(0,96.6)$,
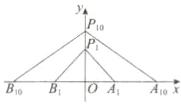
所以 $k_{A_{10}P_{10}}=\frac{96.6 - 0}{0 - 230}=-0.42$,$k_{B_{10}P_{10}}=\frac{96.6 - 0}{0 + 230}=0.42$,
即最长拉索所在直线的斜率为 $\pm0.42$. 故选 B.
B 如图,以 $O$ 为原点建系,
因为最短拉索的两个锚 $P_{1}$,$A_{1}$ 满足 $|OP_{1}| = 57\ m$,$|OA_{1}| = 86\ m$,
且拉索上端相邻两个锚的间距 $|P_{i}P_{i + 1}|(i = 1,2,3,\cdots,9)$ 均为 $4.4\ m$,拉索下端相邻两个锚的间距 $|A_{i}A_{i + 1}|(i = 1,2,3,\cdots,9)$ 均为 $16\ m$,
则 $|OA_{10}| = |OA_{1}|+|A_{1}A_{10}| = 86 + 9\times16 = 230\ m$,即点 $A_{10}(230,0)$,同理 $B_{10}(-230,0)$,
又 $|OP_{10}| = |OP_{1}|+|P_{1}P_{10}| = 57 + 9\times4.4 = 96.6\ m$,即点 $P_{10}(0,96.6)$,

所以 $k_{A_{10}P_{10}}=\frac{96.6 - 0}{0 - 230}=-0.42$,$k_{B_{10}P_{10}}=\frac{96.6 - 0}{0 + 230}=0.42$,
即最长拉索所在直线的斜率为 $\pm0.42$. 故选 B.
16.(开放题)若直线l的倾斜角为$\frac{3\pi}{4}$,则l的一个方向向量$\boldsymbol{d}$可以是________.(只需填写一个)
答案:
$(1,-1)$(答案不唯一)
解析 直线 $l$ 的倾斜角为 $\frac{3\pi}{4}$,故直线的斜率 $k = \tan\frac{3\pi}{4}=-1$,故方向向量的横、纵坐标之比为 $-1$,故 $\boldsymbol{d}$ 可以是 $(1,-1)$.
解析 直线 $l$ 的倾斜角为 $\frac{3\pi}{4}$,故直线的斜率 $k = \tan\frac{3\pi}{4}=-1$,故方向向量的横、纵坐标之比为 $-1$,故 $\boldsymbol{d}$ 可以是 $(1,-1)$.
查看更多完整答案,请扫码查看


