《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

1.（2024·河北唐山一中月考）直线$y = - 3x + 5$不经过的象限为 （ ）
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： 由斜率为负，在y轴上的截距为5,易知直线不过第三象限，故选C.

2. 已知直线$l:y = x\sin\theta+\cos\theta$的图象如图所示，则角$\theta$是 （ ）

A. 第一象限角
B. 第二象限角
C. 第三象限角
D. 第四象限角

答案： 结合图象易知,sinθ＜0,cosθ＞0,则角θ是第四象限角.

3. $a = - 3$是直线$l_1:ax+(1 - a)y - 3 = 0$与直线$l_2:(a - 1)x+(2a + 3)y - 2 = 0$互相垂直的 （ ）
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件

答案： 因为直线l₁:ax+(1−a)y−3=0与直线l₂:(a−1)x +(2a+3)y−2=0互相垂直,所以a(a−1)+(1−a)·(2a+3)=0,解得a=1或a=−3,所以a=−3是直线l₁:ax+(1−a)y−3=0与直线l₂:(a−1)x+(2a+3)y −2=0互相垂直的充分不必要条件.故选A.

4. 直线$l$过点$A(3,4)$，且与点$B( - 3,2)$的距离最远，则直线$l$的方程是 （ ）
A. $3x - y - 5 = 0$
B. $x - 3y + 9 = 0$
C. $3x + y - 13 = 0$
D. $x + 3y - 15 = 0$

答案：
∵直线l过点A(3,4)且与点B(−3,2)的距离最远,
∴直线l的斜率为$\frac{−1}{k_{AB}}$=$\frac{−1}{\frac{4 - 2}{3 + 3}}$=−3,
∴直线l的方程为y−4=−3(x−3),即3x+y−13=0,故选C.

5.（多选）下列说法正确的是 （ ）
A. 截距相等的直线都可以用方程$\frac{x}{a}+\frac{y}{a}=1$表示
B. 方程$x + my - 2 = 0(m\in\mathbf{R})$能表示平行于$y$轴的直线
C. 经过点$P(1,1)$，倾斜角为$\theta$的直线方程为$y - 1=\tan\theta(x - 1)$
D. 经过两点$P_1(x_1,y_1)$，$P_2(x_2,y_2)$的直线方程为$(y_2 - y_1)(x - x_1)-(x_2 - x_1)(y - y_1)=0$

答案： 若直线过原点，横、纵截距都为零，则不能用方程$\frac{x}{a}$+$\frac{y}{a}$=1表示,所以A不正确;当m=0时，方程为x=2,可表示平行于y轴的直线,所以B正确;若直线的倾斜角为90°,则该直线的斜率不存在，不能用y−1=tanθ(x−1)表示,所以C不正确;设点P(x,y)是经过两点P₁(x₁,y₁),P₂(x₂,y₂)的直线上的任意一点,则$\overrightarrow{P_1P_2}$//$\overrightarrow{P_1P}$,可得(y₂−y₁)(x−x₁)−(x₂−x₁)(y−y₁)=0,所以D正确.故选BD.

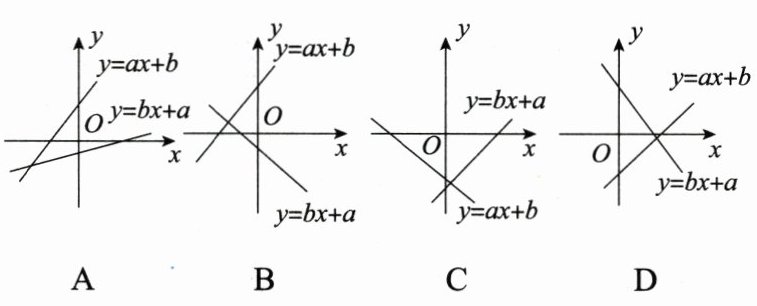
6. 方程$y = ax + b$和$y = bx + a$表示的直线可能是 （ ）

答案： 若直线y=ax+b经过第一、二、三象限,则a＞0,b＞0,从而直线y=bx+a也要经过第一、二、三象限,所以A、B选项错误;若直线y=ax+b经过第二、三、四象限,则a＜0,b＜0,从而直线y=bx+a也要经过第二、三、四象限，所以C选项错误;若直线y=ax+b经过第一、三、四象限,则a＞0,b＜0,从而直线y=bx+a要经过第一、二、四象限，所以D选项正确.

7. 已知直线$\frac{x}{a}+\frac{y}{b}=1$经过第一、二、三象限，且其斜率小于1，则下列不等式中一定正确的是 （ ）
A. $|a|\lt|b|$
B. $\sqrt{-a}＞\sqrt{b}$
C. $(b - a)(b + a)＞0$
D. $\frac{1}{a}＞\frac{1}{b}$

答案： 直线$\frac{x}{a}$+$\frac{y}{b}$=1经过第一、二、三象限,则a＜0,b＞0,由直线的斜率小于1,知0＜−$\frac{b}{a}$＜1,结合a＜0,可得a＜0＜b＜−a,则|a|＞|b|,选项A错误;由幂函数的单调性可知$\sqrt{−a}$＞$\sqrt{b}$,选项B正确;因为b−a＞0,b+a＜0,所以(b−a)(b+a)＜0,选项C错误;a＜0,b＞0,则$\frac{1}{a}$＜$\frac{1}{b}$,选项D错误.故选B.

8. 已知直线$l_1:ax + y - 2 = 0$，$l_2:(a + 3)x - 2by + 1 = 0(a＞0,b＞0)$互相垂直，则$\frac{a}{b}$的取值范围为 （ ）
A. $(0,\frac{1}{3})$
B. $(0,\frac{2}{3})$
C. $(\frac{1}{3},1)$
D. $(3,+\infty)$

答案：
∵直线l₁:ax+y−2=0,l₂:(a+3)x−2by+1=0(a＞0,b＞0)互相垂直,
∴a(a+3)−2b=0,
∴$\frac{a}{b}$=$\frac{2}{a+3}$.
∵a＞0,b＞0,
∴$\frac{2}{a+3}$∈(0,$\frac{2}{3}$).
∴$\frac{a}{b}$的取值范围为(0,$\frac{2}{3}$).故选B.

9. 已知直线$l$与直线$y=\frac{1}{2}x + 4$互相垂直，直线$l$与直线$y = x + 6$在$y$轴上的截距相等，则直线$l$的方程为__________.

答案： 因为直线l与直线y=$\frac{1}{2}$x+4互相垂直，所以直线l的斜率k=−2.又因为直线y=x+6在y轴上的截距为6,所以直线l在y轴上的截距为6,所以直线l的方程为y=−2x+6.

10. 直线$(2a^2 - 7a + 3)x+(a^2 - 9)y + 3a^2 = 0$的倾斜角为$45^{\circ}$，则实数$a =$________.

答案： 由题意知斜率存在，倾斜角为45°,即k=1,所以a²−9≠0,−$\frac{2a²−7a+3}{a²−9}$=1,解得a=−$\frac{2}{3}$或3(舍去),所以a=−$\frac{2}{3}$.

11. 若直线$l$过点$( - 3,4)$，且在两坐标轴上的截距之和为12，则直线$l$的方程为____________________.

答案： 由题意可设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a≠0,b≠0),且a+b=12①.因为直线l过点(−3,4),所以$\frac{−3}{a}$+$\frac{4}{b}$=1②.由①②解得$\begin{cases}a = 9\\b = 3\end{cases}$或$\begin{cases}a = - 4\\b = 16\end{cases}$,故直线l的方程为$\frac{x}{9}$+$\frac{y}{3}$=1或$\frac{x}{−4}$+$\frac{y}{16}$=1,即x+3y−9=0或4x−y+16=0.

12.（2024·福建龙岩一中月考）直线$l$过点$(4,1)$且与$x$轴、$y$轴的正半轴分别交于$A$，$B$两点，$O$为坐标原点，则$\triangle AOB$面积的最小值为________，当$\triangle AOB$的面积取最小值时，直线$l$的一般式方程是__________.

答案： 设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a＞0,b＞0),因为直线l过点(4,1),所以$\frac{4}{a}$+$\frac{1}{b}$=1.又$\frac{4}{a}$+$\frac{1}{b}$≥2$\sqrt{\frac{4}{a}\times\frac{1}{b}}$,所以1≥2$\sqrt{\frac{4}{ab}}$,即ab≥16,当且仅当$\frac{4}{a}$=$\frac{1}{b}$,即a=8,b=2时取等号,所以(S△AOB)min=$\frac{1}{2}$×16=8,此时直线l的方程为$\frac{x}{8}$+$\frac{y}{2}$=1,即x+4y−8=0.

13.（2023·浙江嘉兴联考）直线$l$经过点$(1,3)$，且________.
（1）求直线$l$的方程；
（2）求直线$l$与坐标轴围成的三角形面积.
试从以下两个条件中任选一个补充在上面的问题中，完成解答.
①与直线$2x - y - 1 = 0$平行.
②直线$l$在$x$轴上的截距为$-\frac{1}{2}$.

答案： 解　
(1)选①,
∵直线l与直线2x−y−1=0平行,
∴可设直线l的方程为2x−y+m=0(m≠−1),把(1,3)代入可得m=1,
∴直线l的方程为2x−y+1=0.选②,
∵直线l经过点(1,3),由题意可知直线的斜率存在，设为k,
∴直线l的方程为y−3=k(x−1).
∵直线l在x轴上的截距为−$\frac{1}{2}$,
∴直线l过点(−$\frac{1}{2}$,0),代入方程可得k=2,
∴直线l的方程为2x−y+1=0.
(2)在直线l:2x−y+1=0中,令x=0可得y=1,令y=0可得x=−$\frac{1}{2}$,
∴直线l与坐标轴围成的三角形面积S=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$.