《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

1. 已知空间向量$\boldsymbol{a}$和$\boldsymbol{b}$的夹角为$120^{\circ}$，且$|\boldsymbol{a}| = 2$，$|\boldsymbol{b}| = 5$，则$(2\boldsymbol{a}-\boldsymbol{b})\cdot\boldsymbol{a}$等于（ ）
A. 12
B. $8 + \sqrt{13}$
C. 4
D. 13

答案： 1.D　(2a−b).a=2a²−b.a=2|a|²−|a||b|.cos120°=2×4−22×5×(−$\frac{1}{2}$)=13.

2.（2023·宁波质检）若$\boldsymbol{a}$，$\boldsymbol{b}$均为非零空间向量，则“$\boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}|\cdot|\boldsymbol{b}|$”是“$\boldsymbol{a}$与$\boldsymbol{b}$共线”的（ ）
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件

答案： 2.A　因为a.b=|a|.|b|UYcos＜a,b＞=1,所以a与b的夹角为0°,所以a与b共线,反之不成立，因为当a与b 反向共线时,a.b=−|a|.|b|,所以“a.b=｜a|.|b|”是“a与b共线”的充分不必要条件.故选A.

3. 已知$|\boldsymbol{a}| = 4$，空间向量$\boldsymbol{e}$为单位向量，$\langle\boldsymbol{a},\boldsymbol{e}\rangle=\frac{2\pi}{3}$，则空间向量$\boldsymbol{a}$在向量$\boldsymbol{e}$方向上的投影向量为（ ）
A. $2\boldsymbol{e}$
B. $-2\boldsymbol{e}$
C. $-\frac{1}{2}\boldsymbol{e}$
D. $\frac{1}{2}\boldsymbol{e}$

答案： 3.B由题意,知|α|=4,le｜=1,＜a,e＞=23,则空间向量a在向量e方向上的投影向量为｜a|cos＜a,e)e=−2e.故选B.

4. 已知两异面直线的方向向量分别为$\boldsymbol{a}$，$\boldsymbol{b}$，且$|\boldsymbol{a}| = |\boldsymbol{b}| = 1$，$\boldsymbol{a}\cdot\boldsymbol{b}=-\frac{1}{2}$，则两直线的夹角为（ ）
A. $30^{\circ}$
B. $60^{\circ}$
C. $120^{\circ}$
D. $150^{\circ}$

答案： 4.B设向量a,b的夹角为0,则cos0=$\frac{a.b}{|a||6|}$=−$\frac{1}{2}$,所以0=120°,则两个方向向量对应的直线的夹角为180°-120°=60°.

5.（多选）如图，已知四边形$ABCD$为矩形，$PA\perp$平面$ABCD$，连接$AC$，$BD$，$PB$，$PC$，$PD$，则下列各组向量中，数量积为零的是（ ）

A. $\overrightarrow{PC}$与$\overrightarrow{AD}$
B. $\overrightarrow{DA}$与$\overrightarrow{PB}$
C. $\overrightarrow{PD}$与$\overrightarrow{AB}$
D. $\overrightarrow{PA}$与$\overrightarrow{CD}$

答案： 5.BCD因为PA⊥平面ABCD,所以PA⊥CD,故PA.CD=0;
　因为AD⊥AB,AD⊥PA,且PA∩AB=A,所以AD⊥平面PAB,又PBC平面PAB,故AD⊥PB,则DA.PB=0;
　同理可得PD.AB=0;
　而PC与AD所成角为∠PCB,显然不垂直,故PC.AD≠0.

6.（2024·河北邢台质检）如图，在一个$120^{\circ}$的二面角的棱上有两点$A$，$B$，线段$AC$，$BD$分别在这个二面角的两个半平面内，且均与棱$AB$垂直. 若$AB = \sqrt{2}$，$AC = 1$，$BD = 2$，则$CD$的长为（ ）

A. 2
B. 3
C. $2\sqrt{3}$
D. 4

答案： 6.B
∵CD=CA+AB+BD,
∴CD2=CA2+AB²+BD²+2CA.AB+2CA.BD+2AB.BD.
∵CA⊥AB,BD⊥AB;'
∴CA.AB=0,AB.BD=0,又CA.BD=|CA||BD|cos(180°−120°)=1×2×$\frac{1}{2}$=1,
∴CD²=1+2+4+2×1=9,
∴CD|=3,故选B.

7. 已知$\boldsymbol{a}$，$\boldsymbol{b}$是两个空间向量，若$|\boldsymbol{a}| = 2$，$|\boldsymbol{b}| = 2$，$|\boldsymbol{a}-\boldsymbol{b}|=\sqrt{7}$，则$\cos\langle\boldsymbol{a},\boldsymbol{b}\rangle =$________.

答案： 7.$\frac{1}{8}$
　解析　将|a−b|=√7两边平方,得(a−b)²=7,即|a{²+|b|²−2a.b=7.因为|a|=2,｜b|=2,所以a.b=$\frac{1}{2}$
　又a.b=｜a｜｜b｜cos(a,b＞,故cos(a,b)=$\frac{1}{8}$.

8. 已知向量$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$两两夹角都是$60^{\circ}$，且$|\boldsymbol{a}| = |\boldsymbol{b}| = |\boldsymbol{c}| = 1$，则$|\boldsymbol{a}-2\boldsymbol{b}+\boldsymbol{c}| =$________.

答案： 8.$\sqrt{3}$
　解析　因为｜a−2b+c{²=a²+4b²+c²−4a.b−4b.c+2a.c=1+4+1−4×cos60°−4×cos60°+2×cos60°=3,所以|a−2b+c｜=$\sqrt{3}$.

9. 如图所示，正三棱锥$A - BCD$，试用向量法证明$AD\perp BC$.

答案： 9.证明　设AB=a,AC=b,AD=c,由题意知｜a|=｜b|=
　|c|且＜a,c＞=(b,c),
∴AD.BC=AD.(AC−AB)=c.(b−a)=b.c−a.c=|b||c|.cos(b,c)−{a||c|cos＜＜a,c＞=0,
∴AD⊥BC,即AD⊥BC.

10.（2024·广东广州期末）如图，已知平行六面体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，底面$ABCD$是边长为 1 的正方形，$AA_{1} = 2$，$\angle A_{1}AB = \angle A_{1}AD = 60^{\circ}$，设$\overrightarrow{AB}=\boldsymbol{a}$，$\overrightarrow{AD}=\boldsymbol{b}$，$\overrightarrow{AA_{1}}=\boldsymbol{c}$.
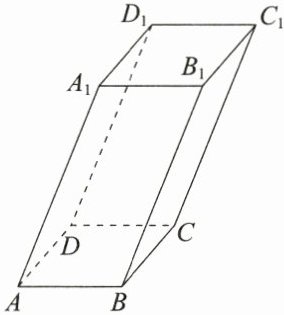
(1)用$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$表示$\overrightarrow{AC_{1}}$，并求$|\overrightarrow{AC_{1}}|$；
(2)求$\overrightarrow{AA_{1}}\cdot\overrightarrow{BD}$.

答案： 10.解　
(1)
∵AB=a,AD=b,AA=c,
∴AC=AB+BC+CC=a+b+c.
∵底面ABCD是边长为1的正方形,AA1=2,∠AAB=∠AlAD=60°,
∴|AC1=　$\sqrt{(a+b+c)²}$
　=　$\sqrt{a²+b²+c²+2a.b+2a.c+2b.c}$
　　　$\sqrt{=/1+1+4+0+2×1×2×\frac{1}{2}}$×2=$\sqrt{10}$二
(2)AA.BD=AA.(AD−AB)=AA.AD−
AA.AB=2×1×$\frac{1}{2}$−2×1×$\frac{1}{2}$=0.